
- •Замкнутая система …
- •Передаточная функция разомкнутой системы имеет вид
- •Цифровая система, описание которой задается передаточной функцией
- •Цифровая система, описание которой задается передаточной функцией
- •Характеристический полином замкнутой системы равен
- •В данном случае передаточная функция замкнутой системы равна
- •В данном случае передаточная функция замкнутой системы равна
- •В данном случае передаточная функция замкнутой системы равна
- •В данном случае передаточная функция замкнутой системы равна
*********************************************
*ОТУ 1.1.01.t2.rtf
*********************************************
!Taskfile ОТУ 1.1.01.#Основные понятия и определения
!DE=ОТУ 1.1.#Основные понятия и определения. Математическое описание непрерывных систем
!Type=2
!Time=2
Экспертные и технологические параметры заданий:
1. Дисциплина: Основы теории управления
2. Объем часов: группа I (от 80 до 170 часов)
3. Дидактическая единица ГОС: Основные понятия и определения. Математическое описание непрерывных систем
4. Тема задания: Основные понятия и определения
5. Уровень сложности: 1 (знать и использовать в типовой учебной ситуации)
6. Ориентировочное время выполнения: 2 минуты
7. Перечень контролируемых учебных элементов
Студент должен знать: основные понятия теории и практики построения систем автоматического управления (САУ), классификацию систем по характеру протекающих процессов;
8. Форма заданий: выбор одного ответа из четырех предложенных
!Task 1
Нули передаточной функции это …
!Solution
Корни числителя называются нулями передаточной функции, так как в точке p=pi передаточная функция обращается в ноль. Корни знаменателя являются корнями характеристического уравнения, и они называются полюсами передаточной функции. В полюсе передаточная функция обращается в бесконечность. Полюсы характеризуют левую часть дифференциального уравнения, а нули правую.
Правильный ответ:
корни числителя.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 208.
!True
корни числителя
!False
корни знаменателя
!False
только неустойчивые корни знаменателя
!False
только неустойчивые корни числителя
!Task 2
Передаточная функция это …
!Solution
Передаточные функции вводятся для сокращения записи дифференциальных уравнений и также представляют собой их символическую запись. Если ввести изображения по Лапласу входных и выходных величин звена, то передаточную функцию можно строго определить как отношение как отношение изображений выходной и входной величин звена при нулевых начальных условиях и равных нулю остальных воздействий на звено.
Правильный ответ:
отношение изображения Лапласа выходного сигнала к изображению Лапласа входного сигнала, вычисленное при нулевых начальных условиях.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 47.
!True
отношение изображения Лапласа выходного сигнала к изображению Лапласа входного сигнала, вычисленное при нулевых начальных условиях
!False
отношение выходного сигнала к входному сигналу
!False
отношение изображения Лапласа входного сигнала к изображению Лапласа выходного сигнала, вычисленное при нулевых начальных условиях
!False
отношение амплитуды выходного сигнала к амплитуде входного сигнала
!Task 3
Относительной степенью передаточной функции называется …
!Solution
Относительной степенью передаточной функции называется разность степеней знаменателя и числителя передаточной функции.
Правильный ответ:
разность степеней знаменателя и числителя
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 47.
!True
разность степеней знаменателя и числителя
!False
разность степеней числителя и знаменателя
!False
степень знаменателя
!False
степень числителя
!Task 4
Полюсы передаточной функции это …
!Solution
Корни числителя называются нулями передаточной функции, так как в точке p=pi передаточная функция обращается в ноль. Корни знаменателя являются корнями характеристического уравнения, и они называются полюсами передаточной функции. В полюсе передаточная функция обращается в бесконечность. Полюсы характеризуют левую часть дифференциального уравнения, а нули правую.
Правильный ответ:
корни знаменателя.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 208.
!True
корни знаменателя
!False
корни числителя
!False
только неустойчивые корни знаменателя
!False
только неустойчивые корни числителя
!Task 5
Частотная передаточная функция это …
!Solution
Частотная передаточная функция W(jw) комплексное число, модуль которого равен отношению амплитуды выходной величины к амплитуде входной, а аргумент – сдвигу фаз выходной величины относительно входной. В более общей формулировке для входного сигнала любого вида частотную передаточную функцию можно представить как отношение изображений (частотных изображений) выходной и входной величины.
Правильный ответ:
Отношение изображения Фурье выходной переменной к изображению Фурье входной переменной при нулевых начальных условиях.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 55.
!True
отношение изображения Фурье выходной переменной к изображению Фурье входной переменной при нулевых начальных условиях
!False
отношение изображения Лапласа выходной переменной к изображению Лапласа входной переменной
!False
зависимость мнимой части частотной передаточной функции от частоты
!False
отношение изображения Фурье входной переменной к изображению Фурье выходной переменной
!Task 6
Переходу от изображения Лапласа к изображению Фурье соответствует уравнение …
!Solution
Частотная передаточная функция W(jw) представляет собой комплексное число, модуль которого равен отношению амплитуды выходной величины к амлитуде входной, а аргумент – сдвигу фаз выходной величины по отношению к входной. В более общей формулировке для входного сигнала любого вида частотную передаточную функцию можно представить как отношение изображений (частотных изображений) выходной и входной величины. Следовательно, частотная передаточная функция легко получается из обычной передаточной функции подстановкой s=jw .
Правильный ответ:

Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 55.
!True
!False

!False

!False
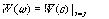
!Task 7
Выражение для определения перерегулирования имеет следующий вид …
!Solution
Склонность
системы к колебаниям, а следовательно,
и запас устойчивости могут быть
охарактеризованы максимальным значением
управляемой величины ym=hmax
или так называемы перерегулированием
равным
 ,
где h∞-
установившееся значение управляемой
величины после завершения переходного
процесса.
,
где h∞-
установившееся значение управляемой
величины после завершения переходного
процесса.
Правильный ответ:
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 201.
!True
!False

!False

!False

!Task 8
Задающим воздействием называется сигнал g*(t), …
!Solution
Величина g*(t) , значение которой должна поддерживать или воспроизводить регулируемая величина, называется задающим воздействием.
Правильный ответ:
определяющий требуемое поведение регулируемой переменной системы.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 11.
!True
определяющий требуемое поведение регулируемой переменной системы
!False
характеризующий текущее значение выходной переменной в режиме слежения
!False
генерируемый внешним задающим блоком (объектом слежения)
!False
выступающий в роли управляющего воздействия следящей системы
!Task 9
Возмущающим воздействием называется сигнал f*(t) , …
!Solution
Возмущающее воздействие f*(t) определяется на основе тех физических законов, которые отражают воздействия внешней среды.
Правильный ответ:
отражающий влияние внешней среды на элементы системы.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 11.
!True
отражающий влияние внешней среды на элементы системы
системы.
!False
характеризующий текущее значение выходной переменной в режиме слежения
!False
генерируемый внешним задающим блоком (объектом слежения)
!False
выступающий в роли задающего воздействия следящей системы
!Task 10
Рассогласованием (ошибкой, отклонением) называется сигнал е(t) = g*(t)-y(t), характеризующий …
!Solution
Разность между заданным и фактическим значением и управляемой величины называется рассогласованием, или ошибкой системы.
Правильный ответ:
текущее значение отклонения выходной переменной от задающего воздействия.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 11.
!True
текущее значение отклонения выходной переменной от задающего воздействия
!False
требуемое направление движения системы с обратной отрицательной связью
!False
текущее значение отклонения входной переменной от задающего воздействия
!False
начальное значение отклонения выходной переменной от задающего воздействия
!Task 11
Переходной функцией называется реакция системы на …
!Solution
Переходная функция, h((t) описывает переходный процесс на выходе системы (звена), возникающий при подаче на ее вход скачкообразного воздействия при величине скачка равной единице при нулевых начальных условиях. Такое входное воздействие называется единичной ступенчатой функцией и обозначается x1(t)=1(t), что соответствует х1=0 при t<0 и x1=1 при t ≥0. Предполагается, что единица имеет ту же размерность, что и физическая величина на входе.
Правильный ответ:
на единичное ступенчатое воздействие при нулевых начальных условиях.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 50.
!True
единичное ступенчатое воздействие при нулевых начальных условиях
!False
импульсное воздействие
!False.
ступенчатое воздействие
!False.
гармоническое воздействие с единичной амплитудой
!Task 12
Весовой функцией называется реакция системы на …
!Solution
Функция веса w(t) представляет собой реакцию звена на дельта- функцию при нулевых начальных условиях импульсную. Дельта-функция представляет собой производную от единичной ступенчатой функции и равна нулю повсюду, кроме точки t=0 , где она стремится к бесконечности.
Правильный ответ:
дельта- функцию при нулевых начальных условиях.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 50.
!True
дельта- функцию при нулевых начальных условиях
!False
единичное ступенчатое воздействие при нулевых начальных условиях
!False.
ступенчатое воздействие при нулевых начальных условиях
!False.
гармоническое воздействие с единичной амплитудой
!Task 13
В задачах стабилизации и слежения требуется обеспечить значения рассогласования e(t) …
!Solution
Системы, поддерживающие постоянное значение управляемой величины при изменяющихся возмущающих воздействиях называются стабилизирующими системами. Системы, управляемая величина которых воспроизводит произвольно изменяющееся задающее воздействие, называются следящими. В обоих случаях задача сводится к ликвидации рассогласования, независимо от причины её вызвавшей.
Правильный ответ:
стремящимся к нулю.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 12.
!True
стремящимся к нулю
!False
постоянным
!False
изменяющимся по заданному закону
!False
стабильными во времени
!Task 14
Системы программного управления обеспечивают значения рассогласования e(t) …
!Solution
Системы, изменяющие управляемую величину по заранее заданной программе, называются программными системами. В них задача сводится к ликвидации рассогласования, независимо от причины её вызвавшей .
Правильный ответ:
стремящимся к нулю.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 12.
!True
стремящимся к нулю
!False
равными постоянной величине
!False
изменяющимся по заданному закону
!False
стабильными во времени
!Task 15
В задачах экстремального управления требуется обеспечить значение рассогласования e(t) …
!Solution
В ряде случаев система сама в процессе управления должна производить поиск такого требуемого значения управляемой величины, которое необходимо в данный момент времени выдерживать, чтобы режим работы управляемого объекта был наивыгоднейшим.
Правильный ответ:
обеспечивающим поиск и поддержание управляемой величины, наиболее выгодной в данный момент для объекта управления.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 12.
!True
обеспечивающее поиск и поддержание управляемой величины, наиболее выгодной в данный момент для объекта управления
!False
максимальным
!False
изменяющимся по заданному закону
!False
стабильным во времени
!Task 16
Непрерывной системой называется такая система, у которой …
!Solution
Системой непрерывного действия или непрерывной системой называется такая система, в каждом из звеньев которой непрерывному изменению входной величины во времени соответствует непрерывное изменение выходной величины.
Правильный ответ:
в каждом её элементе непрерывному изменению входной величины во времени
соответствует непрерывное изменение выходной величины
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 15.
!True
в каждом её элементе непрерывному изменению входной величины во времени
соответствует непрерывное изменение выходной величины
!False
процесс слежения ведется непрерывно
!False
происходит непрерывное изменение задающих и возмущающих воздействий
!False
происходит непрерывное изменение параметров отдельных звеньев
!Task 17
Дискретной системой называется такая система, в которой …
!Solution
Системой дискретного действия, или дискретной системой называется такая система, в которой хотя бы в одном звене при непрерывном изменении входной величины выходная величина изменяется не непрерывно, а имеет вид отдельных импульсов, появляющихся через некоторые промежутки времени. Звено, преобразующее непрерывный входной сигнал в последовательность импульсов, называется импульсным элементом или импульсным модулятором. К дискретным также относятся системы с цифровыми вычислительными устройствами.
Правильный ответ:
хотя бы одно из звеньев преобразует непрерывно изменяющийся входной сигнал в импульсный.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 16.
!True
хотя бы одно из звеньев преобразует непрерывно изменяющийся входной сигнал в импульсный
!False
входные и выходные сигналы всех звеньев являются дискретными
!False
в качестве задающего устройства используется управляющая вычислительная машина
!False
отсутствуют непрерывные звенья
!Task 18
Система называется линейной, если …
!Solution
Линейной системой называется такая система, поведение всех звеньев которой вполне описывается линейными уравнениями (алгебраическими, дифференциальными или разностными). Для этого необходимо прежде всего, чтобы статические характеристики всех звеньев системы были линейными, т.е. имели вид прямой линии.
Правильный ответ:
все её элементы описываются линейными уравнениями (алгебраическими, дифференциальными или разностными).
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 16.
!True
все её элементы описываются линейными уравнениями (алгебраическими, дифференциальными или разностными)
!False
задающие и возмущающие воздействия изменяются по линейным законам
!False
хотя бы одно её звено описывается линейным дифференциальным уравнением
!False
управляющее воздействие изменяется по линейному закону
!Task 19
Система называется нелинейной, если …
!Solution
Нелинейной системой называется такая система, в которой хотя бы в одном элеменье нарушается линейность статической характеристики или же имеет место любое другое нарушение уравнений динамики звена (произведение переменных или их производных, корень, квадрат или более высокая степень переменной, любая другая нелинейная связь переменных и их производных.
Правильный ответ:
хотя бы один из её элементов описывается нелинейным уравнением (алгебраическими, дифференциальными или разностными).
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 17.
!True
хотя бы один из её элементов описывается нелинейным уравнением (алгебраическими, дифференциальными или разностными)
!False
задающие и возмущающие воздействия изменяются по нелинейным законам
!False
управляемая величина изменяется по нелинейному закону
!False
управляющее воздействие изменяется по нелинейному закону
!Task 20
Многомерной системой управления называется система, …
!Solution
Многомерная система предполагает наличие многомерного объекта управления, который характеризуется существованием нескольких входов (точек приложения управляющих и возмущающих воздействий) и нескольких выходов, определяемых управляемыми величинами.
Правильный ответ:
в которой объект управления имеет несколько входов и выходов.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 17.
!True
в которой объект управления имеет несколько входов и выходов
!False
с независимыми каналами
!False
с взаимосвязанными каналами
!False
в которой динамика объекта управления характеризуется несколькими независимыми переменными
!Task 21
Объект называется полностью управляемым, если …
!Solution
Объект называется полностью управляемым, если существует такое управляющее воздействие u(t), определенное на конечном интервале времени, которое переводит его из любого начального состояния x(t0)в любое заданное конечное состояние x(tk). Управляющее воздействие должно прямо или косвенно влиять на все переменные состояния.
Правильный ответ:
существует такое управляющее воздействие u(t), определенное на конечном интервале времени, которое переводит его из любого начального состояния x(t0)в любое заданное конечное состояние x(tk).
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 110.
!True
существует такое управляющее воздействие u(t), определенное на конечном интервале времени, которое переводит его из любого начального состояния x(t0)в любое заданное конечное состояние x(tk)
!False
если составлена его математическое описание
!False
может быть измерена управляемая величина
!False
все возмущающие воздействия внешней среды могут быть измерены
!Task 22
Автоматическое управление – это …
!Solution
Автоматическое управление в технике, совокупность действий, направленных на поддержание или улучшение функционирования управляемого объекта без непосредственного участия человека в соответствии с заданной целью управления.
Правильный ответ:
целенаправленное воздействие на объект, приводящее к заданному изменению его состояния.
Литература: Большая советская энциклопедия.
!True
целенаправленное воздействие на объект, приводящее к заданному изменению его состояния
!False
автоматическое воздействие на объект, приводящее к улучшению его состояния
!False
заданное воздействие на объект, приводящее к целенаправленному изменению его состояния
!False
целенаправленное изменение свойств объекта (управляемого процесса), приводящее к улучшению его состояния
!Task 23
Системы автоматического управления – это …
!Solution
Система управления — систематизированный набор средств влияния на подконтрольный объект для достижения определённых целей данным объектом без участия человека в контуре управления
Правильный ответ:
системы, выполняющие свои функции автоматически (без участия человека).
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с.
!True
системы, выполняющие свои функции автоматически (без участия человека)
!False
системы, в состав которых входят различные автоматы
!False
автоматизированные системы, часть функций которых выполняется автоматически, а часть оператором
!False
технические и природные системы, выполняющие свои функции с помощью автоматических устройств управления
!Task 24
Автоматизированные системы - это системы, …
!Solution
Автоматизированная система управления или АСУ — комплекс аппаратных и программных средств, предназначенный для управления различными процессами в рамках технологического процесса, производства, предприятия
с участием человека в контуре управления
Правильный ответ:
предназначенные для управления технологическими процессами с участием человека
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с.
!True
предназначенные для управления технологическими процессами с участием человека
!False
выполняющие свои функции автоматически (без участия человека)
!False
выполняющие свои функции с помощью автоматизированных устройств
!False
обеспечивающие целенаправленное изменение свойств объекта, приводящее к улучшению его состояния
!Task 25
Если H1(s) - передаточная функция прямой связи, а H2(s) - передаточная функция отрицательной обратной связи, то результирующая передаточная функция будет определяться выражением …
!Solution
Пусть W1(s) – передаточная функция звена в прямой цепи, а W2(s) – звено в обратной связи, а обратная связь может быть как положительной, так и отрицательной. Тогда результирующую передаточную функцию можно найти по формуле:

Здесь знак минус относится к положительной, а знак плюс - к отрицательной обратной связи.
Правильный
ответ:

Литература: 1. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 93.
!True

!False

!False

!False

!END
*********************************************
*ОТУ 1.1.02.t2.rtf
*********************************************
!Taskfile ОТУ 1.1.02.#Связь между дифференциальными уравнениями и передаточными функциями
!DE=ОТУ 1.1.#Основные понятия и определения. Математическое описание непрерывных систем
!Type=2
!Time=2
Экспертные и технологические параметры заданий:
1. Дисциплина: Основы теории управления
2. Объем часов: группа I (от 80 до 170 часов)
3. Дидактическая единица ГОС: Основные понятия и определения. Математическое описание непрерывных систем
4. Тема задания: Связь между дифференциальными уравнениями и передаточными функциями
5. Уровень сложности: 2 (знать и уметь использовать в типовой учебной ситуации)
6. Ориентировочное время выполнения: 2 минуты
7. Перечень контролируемых учебных элементов
Студент должен знать: формы задания уравнений движения САУ
уметь: : устанавливать соответствие между дифференциальными уравнениями движения и передаточными функциями разомкнутых и замкнутых систем
8. Форма заданий: выбор одного ответа из четырех предложенных
!Task 1
Дифференциальным уравнением соответствующим передаточной функции вида:

является …
!Solution
Дифференциальные уравнения записываются так, чтобы выходная величина и её производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Считая, условно, оператор дифференцирования p=d/dt алгебраической величиной, решим данное уравнение относительно выходной величины. Полученное выражение представляет собой символическую запись дифференциального уравнения и вводиться для сокращения её записи. Более строго передаточная функция определяется через изображения Лапласа.
Если ввести изображения по Лапласу входных и выходных величин, где s=c+jw – комплексная величина, то передаточную функцию можно строго определить как отношение изображений выходной и входной величины звена при нулевых начальных условиях и равных нулю остальных воздействиях на звено.
Правильный
ответ:

Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 44-47.
!True

!False

!False

!False

!Task 2
Дифференциальным уравнением соответствующим передаточной функции вида:

является …
!Solution
Дифференциальные уравнения записываются так, чтобы выходная величина и её производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Считая, условно, оператор дифференцирования p=d/dt алгебраической величиной, решим данное уравнение относительно выходной величины. Полученное выражение представляет собой символическую запись дифференциального уравнения и вводиться для сокращения её записи. Более строго передаточная функция определяется через изображения Лапласа.
Если
ввести изображения по Лапласу входных
и выходных величин, где s=c+jw
– комплексная величина, то передаточную
функцию можно строго определить как
отношение изображений выходной и
входной величины звена при нулевых
начальных условиях и равных нулю
остальных воздействиях на звено.
Правильный
ответ:
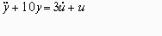
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 44-47.
!True

!False

!False

!False
!Task 3
Дифференциальным уравнением соответствующим передаточной функции вида …

является:
!Solution
Дифференциальные уравнения записываются так, чтобы выходная величина и её производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Считая, условно, оператор дифференцирования p=d/dt алгебраической величиной, решим данное уравнение относительно выходной величины. Полученное выражение представляет собой символическую запись дифференциального уравнения и вводиться для сокращения её записи. Более строго передаточная функция определяется через изображения Лапласа.
Если
ввести изображения по Лапласу входных
и выходных величин, где s=c+jw
– комплексная величина, то передаточную
функцию можно строго определить как
отношение изображений выходной и
входной величины звена при нулевых
начальных условиях и равных нулю
остальных воздействиях на звено
Правильный
ответ:

Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 44-47.
!True
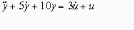
!False
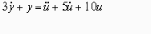
!False

!False
!Task 4
Дифференциальным уравнением соответствующим передаточной функции вида …

является:
!Solution
Дифференциальные уравнения записываются так, чтобы выходная величина и её производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Считая, условно, оператор дифференцирования p=d/dt алгебраической величиной, решим данное уравнение относительно выходной величины. Полученное выражение представляет собой символическую запись дифференциального уравнения и вводиться для сокращения её записи. Более строго передаточная функция определяется через изображения Лапласа.
Если
ввести изображения по Лапласу входных
и выходных величин, где s=c+jw
– комплексная величина, то передаточную
функцию можно строго определить как
отношение изображений выходной и
входной величины звена при нулевых
начальных условиях и равных нулю
остальных воздействиях на звено
Правильный
ответ:

Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 44-47.
!True

!False

!False

!False
!Task 5
Дифференциальным уравнением соответствующим передаточной функции вида …

является
!Solution
Дифференциальные уравнения записываются так, чтобы выходная величина и её производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Считая, условно, оператор дифференцирования p=d/dt алгебраической величиной, решим данное уравнение относительно выходной величины. Полученное выражение представляет собой символическую запись дифференциального уравнения и вводиться для сокращения её записи. Более строго передаточная функция определяется через изображения Лапласа.
Если ввести изображения по Лапласу входных и выходных величин, где s=c+jw – комплексная величина, то передаточную функцию можно строго определить как отношение изображений выходной и входной величины звена при нулевых начальных условиях и равных нулю остальных воздействиях на звено
Правильный ответ:

Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 44-47.
!True

!False

!False

!False

!Task 6
Передаточной функцией, соответствующей дифференциальному уравнению вида …
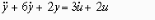
где y - выходная переменная, u - сигнал управления, k – коэффициент передачи;
является
!Solution
Дифференциальные уравнения записываются так, чтобы выходная величина и её производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Считая, условно, оператор дифференцирования p=d/dt алгебраической величиной, решим данное уравнение относительно выходной величины. Полученное выражение представляет собой символическую запись дифференциального уравнения и вводиться для сокращения её записи. Более строго передаточная функция определяется через изображения Лапласа.
Если
ввести изображения по Лапласу входных
и выходных величин, где s=c+jw
– комплексная величина, то передаточную
функцию можно строго определить как
отношение изображений выходной и
входной величины звена при нулевых
начальных условиях и равных нулю
остальных воздействиях на звено
Правильный
ответ:

Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 44-47.
!True

!False

!False

!False

!Task 7
Передаточной функцией, соответствующей дифференциальному уравнению вида …

где y - выходная переменная, u - сигнал управления, k – коэффициент передачи;
является
!Solution
Дифференциальные уравнения записываются так, чтобы выходная величина и её производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Считая, условно, оператор дифференцирования p=d/dt алгебраической величиной, решим данное уравнение относительно выходной величины. Полученное выражение представляет собой символическую запись дифференциального уравнения и вводиться для сокращения её записи. Более строго передаточная функция определяется через изображения Лапласа.
Если
ввести изображения по Лапласу входных
и выходных величин, где s=c+jw
– комплексная величина, то передаточную
функцию можно строго определить как
отношение изображений выходной и
входной величины звена при нулевых
начальных условиях и равных нулю
остальных воздействиях на звено
Правильный
ответ:

Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 44-47.
!True

!False

!False

!False

!Task 8
Передаточной функцией, соответствующей дифференциальному уравнению вида …

где y - выходная переменная, u - сигнал управления, k – коэффициент передачи;
является
!Solution
Дифференциальные уравнения записываются так, чтобы выходная величина и её производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Считая, условно, оператор дифференцирования p=d/dt алгебраической величиной, решим данное уравнение относительно выходной величины. Полученное выражение представляет собой символическую запись дифференциального уравнения и вводиться для сокращения её записи. Более строго передаточная функция определяется через изображения Лапласа.
Если
ввести изображения по Лапласу входных
и выходных величин, где s=c+jw
– комплексная величина, то передаточную
функцию можно строго определить как
отношение изображений выходной и
входной величины звена при нулевых
начальных условиях и равных нулю
остальных воздействиях на звено
Правильный
ответ:

Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 44-47.
!True

!False

!False

!False

!Task 9
Передаточной функцией, соответствующей дифференциальному уравнению вида …

где y - выходная переменная, u - сигнал управления, k – коэффициент передачи;
является
!Solution
Дифференциальные уравнения записываются так, чтобы выходная величина и её производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Считая, условно, оператор дифференцирования p=d/dt алгебраической величиной, решим данное уравнение относительно выходной величины. Полученное выражение представляет собой символическую запись дифференциального уравнения и вводиться для сокращения её записи. Более строго передаточная функция определяется через изображения Лапласа.
Если
ввести изображения по Лапласу входных
и выходных величин, где s=c+jw
– комплексная величина, то передаточную
функцию можно строго определить как
отношение изображений выходной и
входной величины звена при нулевых
начальных условиях и равных нулю
остальных воздействиях на звено.
Правильный
ответ:

Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 44-47.
!True
!False

!False

!False

!Task 10
Передаточной функцией, соответствующей дифференциальному уравнению вида …
 ,
,
где y - выходная переменная, u - сигнал управления, k – коэффициент передачи.
является
!Solution
Дифференциальные уравнения записываются так, чтобы выходная величина и её производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Считая, условно, оператор дифференцирования p=d/dt алгебраической величиной, решим данное уравнение относительно выходной величины. Полученное выражение представляет собой символическую запись дифференциального уравнения и вводиться для сокращения её записи. Более строго передаточная функция определяется через изображения Лапласа.
Если ввести изображения по Лапласу входных и выходных величин, где s=c+jw – комплексная величина, то передаточную функцию можно строго определить как отношение изображений выходной и входной величины звена при нулевых начальных условиях и равных нулю остальных воздействиях на звено Правильный ответ:

Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 44-47.
!True
!False

!False

!False

!Task 11
Дифференциальным уравнением соответствующим передаточной функции вида …

является
!Solution
Дифференциальные уравнения записываются так, чтобы выходная величина и её производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Считая, условно, оператор дифференцирования p=d/dt алгебраической величиной, решим данное уравнение относительно выходной величины. Полученное выражение представляет собой символическую запись дифференциального уравнения и вводиться для сокращения её записи. Более строго передаточная функция определяется через изображения Лапласа.
Если ввести изображения по Лапласу входных и выходных величин, где s=c+jw – комплексная величина, то передаточную функцию можно строго определить как отношение изображений выходной и входной величины звена при нулевых начальных условиях и равных нулю остальных воздействиях на звено.
Правильный
ответ:

Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с.,стр. 44-47.
!True
!False

!False
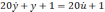
!False

!Task 12
Дифференциальным уравнением соответствующим передаточной функции вида …
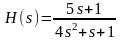
является
!Solution
Дифференциальные уравнения записываются так, чтобы выходная величина и её производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Считая, условно, оператор дифференцирования p=d/dt алгебраической величиной, решим данное уравнение относительно выходной величины. Полученное выражение представляет собой символическую запись дифференциального уравнения и вводиться для сокращения её записи. Более строго передаточная функция определяется через изображения Лапласа.
Если ввести изображения по Лапласу входных и выходных величин, где s=c+jw – комплексная величина, то передаточную функцию можно строго определить как отношение изображений выходной и входной величины звена при нулевых начальных условиях и равных нулю остальных воздействиях на звено.
Правильный
ответ:

Литература:Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с.,стр. 44-47.
!True
!False

!False

!False

!Task 13
Дифференциальным уравнением соответствующим передаточной функции вида …

является
!Solution
Дифференциальные уравнения записываются так, чтобы выходная величина и её производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Считая, условно, оператор дифференцирования p=d/dt алгебраической величиной, решим данное уравнение относительно выходной величины. Полученное выражение представляет собой символическую запись дифференциального уравнения и вводиться для сокращения её записи. Более строго передаточная функция определяется через изображения Лапласа.
Если
ввести изображения по Лапласу входных
и выходных величин, где s=c+jw
– комплексная величина, то передаточную
функцию можно строго определить как
отношение изображений выходной и
входной величины звена при нулевых
начальных условиях и равных нулю
остальных воздействиях на звено
Правильный
ответ:

Литература:Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с.,стр. 44-47.
!True
!False
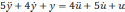
!False
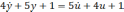
!False

!Task 14
Дифференциальным уравнением соответствующим передаточной функции вида …

является:
!Solution
Дифференциальные уравнения записываются так, чтобы выходная величина и её производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Считая, условно, оператор дифференцирования p=d/dt алгебраической величиной, решим данное уравнение относительно выходной величины. Полученное выражение представляет собой символическую запись дифференциального уравнения и вводиться для сокращения её записи. Более строго передаточная функция определяется через изображения Лапласа.
Если
ввести изображения по Лапласу входных
и выходных величин, где s=c+jw
– комплексная величина, то передаточную
функцию можно строго определить как
отношение изображений выходной и
входной величины звена при нулевых
начальных условиях и равных нулю
остальных воздействиях на звено
Правильный
ответ:

Литература:Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с.,стр. 44-47.
!True
!False

!False
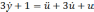
!False

!Task 15
Дифференциальным уравнением соответствующим передаточной функции вида …
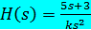
является:
!Solution
Дифференциальные уравнения записываются так, чтобы выходная величина и её производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Считая, условно, оператор дифференцирования p=d/dt алгебраической величиной, решим данное уравнение относительно выходной величины. Полученное выражение представляет собой символическую запись дифференциального уравнения и вводиться для сокращения её записи. Более строго передаточная функция определяется через изображения Лапласа.
Если ввести изображения по Лапласу входных и выходных величин, где s=c+jw – комплексная величина, то передаточную функцию можно строго определить как отношение изображений выходной и входной величины звена при нулевых начальных условиях и равных нулю остальных воздействиях на звено
Правильный
ответ:

Литература:Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с.,стр. 44-47.
!True
!False

!False

!False

!Task 16
Передаточной функцией, соответствующей дифференциальному уравнению вида …
где y - выходная переменная, u - сигнал управления, k – коэффициент передачи;
является
!Solution
Дифференциальные уравнения записываются так, чтобы выходная величина и её производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Считая, условно, оператор дифференцирования p=d/dt алгебраической величиной, решим данное уравнение относительно выходной величины. Полученное выражение представляет собой символическую запись дифференциального уравнения и вводиться для сокращения её записи. Более строго передаточная функция определяется через изображения Лапласа.
Если
ввести изображения по Лапласу входных
и выходных величин, где s=c+jw
– комплексная величина, то передаточную
функцию можно строго определить как
отношение изображений выходной и
входной величины звена при нулевых
начальных условиях и равных нулю
остальных воздействиях на звено
Правильный
ответ:

Литература:Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с.,стр. 44-47.
!True
!False
!False
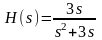
!False
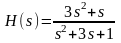
!Task 17
Передаточной функцией, соответствующей дифференциальному уравнению вида …

где y - выходная переменная, u - сигнал управления, k – коэффициент передачи;
является
!Solution
Дифференциальные уравнения записываются так, чтобы выходная величина и её производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Считая, условно, оператор дифференцирования p=d/dt алгебраической величиной, решим данное уравнение относительно выходной величины. Полученное выражение представляет собой символическую запись дифференциального уравнения и вводиться для сокращения её записи. Более строго передаточная функция определяется через изображения Лапласа.
Если
ввести изображения по Лапласу входных
и выходных величин, где s=c+jw
– комплексная величина, то передаточную
функцию можно строго определить как
отношение изображений выходной и
входной величины звена при нулевых
начальных условиях и равных нулю
остальных воздействиях на звено
Правильный
ответ:

Литература:Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с.,стр. 44-47.
!True
!False

!False

!False

!Task 18
Передаточной функцией, соответствующей дифференциальному уравнению вида …
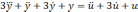
где y - выходная переменная, u - сигнал управления, k – коэффициент передачи;
является
!Solution
Дифференциальные уравнения записываются так, чтобы выходная величина и её производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Считая, условно, оператор дифференцирования p=d/dt алгебраической величиной, решим данное уравнение относительно выходной величины. Полученное выражение представляет собой символическую запись дифференциального уравнения и вводиться для сокращения её записи. Более строго передаточная функция определяется через изображения Лапласа.
Если ввести изображения по Лапласу входных и выходных величин, где s=c+jw– комплексная величина, то передаточную функцию можно строго определить как отношение изображений выходной и входной величины звена при нулевых начальных условиях и равных нулю остальных воздействиях на звено.
Правильный
ответ:

Литература:Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с.,стр. 44-47.
!True
!False

!False

!False

!Task 19
Передаточной функцией, соответствующей дифференциальному уравнению вида …

где y - выходная переменная, u - сигнал управления, k – коэффициент передачи;
является
!Solution
Дифференциальные уравнения записываются так, чтобы выходная величина и её производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Считая, условно, оператор дифференцирования p=d/dt алгебраической величиной, решим данное уравнение относительно выходной величины. Полученное выражение представляет собой символическую запись дифференциального уравнения и вводиться для сокращения её записи. Более строго передаточная функция определяется через изображения Лапласа.
Если
ввести изображения по Лапласу входных
и выходных величин, где s=c+jw
– комплексная величина, то передаточную
функцию можно строго определить как
отношение изображений выходной и
входной величины звена при нулевых
начальных условиях и равных нулю
остальных воздействиях на звено
Правильный
ответ:

Литература:Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с.,стр. 44-47.
!True
!False

!False

!False

!Task 20
Передаточной функцией, соответствующей дифференциальному уравнению вида …
 ,
,
где y - выходная переменная, u - сигнал управления, k – коэффициент передачи;
является:
!Solution
Дифференциальные уравнения записываются так, чтобы выходная величина и её производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Считая, условно, оператор дифференцирования p=d/dt алгебраической величиной, решим данное уравнение относительно выходной величины. Полученное выражение представляет собой символическую запись дифференциального уравнения и вводиться для сокращения её записи. Более строго передаточная функция определяется через изображения Лапласа.
Если
ввести изображения по Лапласу входных
и выходных величин, где s=c+jw
– комплексная величина, то передаточную
функцию можно строго определить как
отношение изображений выходной и
входной величины звена при нулевых
начальных условиях и равных нулю
остальных воздействиях на звено
Правильный
ответ:

Литература:Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с.,стр. 44-47.
!True
!False

!False
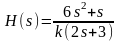
!False

!Task 21
Относительная степень передаточной функции

равна …
!Solution
Относительная степень передаточной функции это разность степеней знаменателя и числителя передаточной функции.
Правильный ответ:
2
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр.47.
!True
2
!False
3
!False
1
!False
0
!Task 22
Относительная степень передаточной функции

равна …
!Solution
Относительная степень передаточной функции это разность степеней знаменателя и числителя передаточной функции.
Правильный ответ:
3
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 47.
!True
3
!False
2
!False
1
!False
0
!Task 23
Относительная степень передаточной функции

равна …
!Solution
Относительная степень передаточной функции это разность степеней знаменателя и числителя передаточной функции.
Правильный ответ:
0
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 47.
!True
0
!False
1
!False
2
!False
3
!Task 24
Нулями передаточной функции вида:

являются …
!Solution
Корни числителя называются нулями передаточной функции, так как в точке p=pi передаточная функция обращается в ноль. Корни знаменателя являются корнями характеристического уравнения, и они называются полюсами передаточной функции. В полюсе передаточная функция обращается в бесконечность. Полюсы характеризуют левую часть дифференциального уравнения, а нули правую.
Правильный ответ:
-3 и 4.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 208.
!True
-3 и 4
!False
3 и 4
!False
0, -2 и 5
!False
0, 2 и 5
!Task 25
Нулями передаточной функции вида:
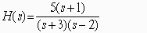
являются …
!Solution
Корни числителя называются нулями передаточной функции, так как в точке p=pi передаточная функция обращается в ноль. Корни знаменателя являются корнями характеристического уравнения, и они называются полюсами передаточной функции. В полюсе передаточная функция обращается в бесконечность. Полюсы характеризуют левую часть дифференциального уравнения, а нули правую.
Правильный ответ:
-1.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 208.
!True
-1
!False
-3 и 2
!False
1
!False
3 и -2
!Task 26
Полюсами передаточной функции вида:
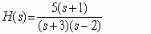
являются …
!Solution
Корни числителя называются нулями передаточной функции, так как в точке p=pi передаточная функция обращается в ноль. Корни знаменателя являются корнями характеристического уравнения, и они называются полюсами передаточной функции. В полюсе передаточная функция обращается в бесконечность. Полюсы характеризуют левую часть дифференциального уравнения, а нули правую.
Правильный ответ:
-3 и 2.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 208.
!True
-3 и 2
!False
3 и 2
!False
-3, 2 и -1
!False
3, -2 и 1
!Task 27
Полюсами передаточной функции вида:

являются …
!Solution
Корни числителя называются нулями передаточной функции, так как в точке p=pi передаточная функция обращается в ноль. Корни знаменателя являются корнями характеристического уравнения, и они называются полюсами передаточной функции. В полюсе передаточная функция обращается в бесконечность. Полюсы характеризуют левую часть дифференциального уравнения, а нули правую.
Правильный ответ:
0 и 2.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 208.
!True
0 и 2
!False
0 и -2
!False
-3
!False
0, -2 и 3
!Task 28
Полюсами передаточной функции вида:

являются …
!Solution
Корни числителя называются нулями передаточной функции, так как в точке p=pi передаточная функция обращается в ноль. Корни знаменателя являются корнями характеристического уравнения, и они называются полюсами передаточной функции. В полюсе передаточная функция обращается в бесконечность. Полюсы характеризуют левую часть дифференциального уравнения, а нули правую.
Правильный ответ:
0, 2 и -5.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 208.
!True
0, 2 и -5
!False
0, -2 и 5
!False
-3 и 4
!False
3 и -4
!Task 29
Передаточной функцией, соответствующей дифференциальному уравнению вида:
 ,
,
является …
!Solution
Дифференциальные уравнения записываются так, чтобы выходная величина и её производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Считая условно оператор дифференцирования p=d/dt алгебраической величиной, решим данное уравнение относительно выходной величины. Полученное выражение представляет собой символическую запись дифференциального уравнения и вводиться для сокращения её записи. Более строго передаточная функция определяется через изображения Лапласа.
Если
ввести изображения по Лапласу входных
и выходных величин, где s=c+jw
– комплексная величина, то передаточную
функцию можно строго определить как
отношение изображений выходной и
входной величины звена при нулевых
начальных условиях и равных нулю
остальных воздействиях на звено
Правильный
ответ:

Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 44-47.
!True
!False

!False
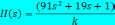
!False

!Task 30
Передаточной функцией, соответствующей дифференциальному уравнению вида:
 ,
,
является …
!Solution
Дифференциальные уравнения записываются так, чтобы выходная величина и её производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Считая условно оператор дифференцирования p=d/dt алгебраической величиной, решим данное уравнение относительно выходной величины. Полученное выражение представляет собой символическую запись дифференциального уравнения и вводиться для сокращения её записи. Более строго передаточная функция определяется через изображения Лапласа.
Если ввести изображения по Лапласу входных и выходных величин, где s=c+jw – комплексная величина, то передаточную функцию можно строго определить как отношение изображений выходной и входной величины звена при нулевых начальных условиях и равных нулю остальных воздействиях на звено Правильный ответ:

Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 44-47.
!True
!False

!False
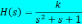
!False

!Task 31
Передаточной функцией, соответствующей дифференциальному уравнению вида:
 ,
,
является …
!Solution
Дифференциальные уравнения записываются так, чтобы выходная величина и её производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Считая условно оператор дифференцирования p=d/dt алгебраической величиной, решим данное уравнение относительно выходной величины. Полученное выражение представляет собой символическую запись дифференциального уравнения и вводиться для сокращения её записи. Более строго передаточная функция определяется через изображения Лапласа.
Если
ввести изображения по Лапласу входных
и выходных величин, где s=c+jw
– комплексная величина, то передаточную
функцию можно строго определить как
отношение изображений выходной и
входной величины звена при нулевых
начальных условиях и равных нулю
остальных воздействиях на звено
Правильный
ответ:

Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 44-47.
!True
!False
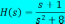
!False

!False

!Task 32
Передаточной функцией, соответствующей дифференциальному уравнению вида:
 ,
,
является …
!Solution
Дифференциальные уравнения записываются так, чтобы выходная величина и её производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Считая условно оператор дифференцирования p=d/dt алгебраической величиной, решим данное уравнение относительно выходной величины. Полученное выражение представляет собой символическую запись дифференциального уравнения и вводиться для сокращения её записи. Более строго передаточная функция определяется через изображения Лапласа.
Если
ввести изображения по Лапласу входных
и выходных величин, где s=c+jw
– комплексная величина, то передаточную
функцию можно строго определить как
отношение изображений выходной и
входной величины звена при нулевых
начальных условиях и равных нулю
остальных воздействиях на звено
Правильный
ответ:

Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 44-47.
!True
!False

!False

!False
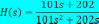
!Task 33
Передаточной функцией, соответствующей дифференциальному уравнению вида:
 ,
,
является …
!Solution
Дифференциальные уравнения записываются так, чтобы выходная величина и её производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Считая условно оператор дифференцирования p=d/dt алгебраической величиной, решим данное уравнение относительно выходной величины. Полученное выражение представляет собой символическую запись дифференциального уравнения и вводиться для сокращения её записи. Более строго передаточная функция определяется через изображения Лапласа.
Если
ввести изображения по Лапласу входных
и выходных величин, где s=c+jw
– комплексная величина, то передаточную
функцию можно строго определить как
отношение изображений выходной и
входной величины звена при нулевых
начальных условиях и равных нулю
остальных воздействиях на звено
Правильный
ответ:

Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 44-47.
!True
!False

!False

!False

!Task 34
Передаточной функцией, соответствующей дифференциальному уравнению вида:
 ,
,
является …
!Solution
Дифференциальные уравнения записываются так, чтобы выходная величина и её производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Считая условно оператор дифференцирования p=d/dt алгебраической величиной, решим данное уравнение относительно выходной величины. Полученное выражение представляет собой символическую запись дифференциального уравнения и вводиться для сокращения её записи. Более строго передаточная функция определяется через изображения Лапласа.
Если
ввести изображения по Лапласу входных
и выходных величин, где s=c+jw
– комплексная величина, то передаточную
функцию можно строго определить как
отношение изображений выходной и
входной величины звена при нулевых
начальных условиях и равных нулю
остальных воздействиях на звено
Правильный
ответ:
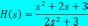
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 44-47.
!True
!False

!False
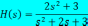
!False
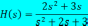
!Task 35
Передаточной функцией, соответствующей дифференциальному уравнению вида:
 ,
,
является …
!Solution
Дифференциальные уравнения записываются так, чтобы выходная величина и её производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Считая условно оператор дифференцирования p=d/dt алгебраической величиной, решим данное уравнение относительно выходной величины. Полученное выражение представляет собой символическую запись дифференциального уравнения и вводиться для сокращения её записи. Более строго передаточная функция определяется через изображения Лапласа.
Если
ввести изображения по Лапласу входных
и выходных величин, где s=c+jw
– комплексная величина, то передаточную
функцию можно строго определить как
отношение изображений выходной и
входной величины звена при нулевых
начальных условиях и равных нулю
остальных воздействиях на звено
Правильный
ответ:

Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 44-47.
!True
!False

!False

!False

!End
*********************************************
*ОТУ 1.1.03.t2.doc
*********************************************
!Taskfile ОТУ 1.1.03.# Частотные передаточные функции и частотные характеристики систем
!DE=ОТУ 1.1.#Основные понятия и определения. Математическое описание непрерывных систем
!Type=2
!Time=2
Экспертные и технологические параметры заданий:
1. Дисциплина: Основы теории управления
2. Объем часов: группа I (от 80 до 170 часов)
3. Дидактическая единица ГОС: Основные понятия и определения. Математическое описание непрерывных систем
4. Тема задания: Частотные передаточные функции и частотные характеристики систем
5. Уровень сложности: 2 (знать и уметь использовать в типовой учебной ситуации)
6. Ориентировочное время выполнения: 2 минуты
7. Перечень контролируемых учебных элементов
Студент должен знать: способы построения различных частотных характеристик систем
уметь: : узнавать частотные характеристики по частотным передаточным функциям
8. Форма заданий: выбор одного ответа из четырех предложенных
!Task 1
Модуль частотной передаточной функции при фиксированной частоте w можно определить как …
!Solution
Частотная передаточная функция W(jw) представляет собой комплексное число, модуль которого равен отношению амплитуды выходной величины к амплитуде входной, а аргумент – сдвигу фаз выходной величины по отношению к входной. Частотная передаточная функция может быть представлена в следующем виде:
Правильный ответ: отношение амплитуды выходного сигнала к амплитуде входного сигнала.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 55.
!True
отношение амплитуды выходного сигнала к амплитуде входного сигнала
!False
произведение амплитуды и фазы выходного сигнала
!False
отношение амплитуды входного сигнала к амплитуде выходного сигнала.
!False
произведение амплитуды выходного сигнала на амплитуду входного сигнала
!Task 2
Аргумент частотной передаточной функции при фиксированной частоте w можно определить как …
!Solution
Частотная передаточная функция W(jw) представляет собой комплексное число, модуль которого равен отношению амплитуды выходной величины к амплитуде входной, а аргумент – сдвигу фаз выходной величины по отношению к входной. Частотная передаточная функция может быть представлена в следующем виде:
Правильный ответ: сдвиг фаз между входным и выходным сигналами.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 55.
!True
сдвиг фаз между входным и выходным сигналами
!False
отношение амплитуды к фазе входного сигнала
!False
модуль частотной передаточной функции
!False
модуль вещественной части частотной передаточной функции
!Task 3
Для построения амплитудно-частотной характеристики необходимо найти …
!Solution
Частотная передаточная функция W(jw) представляет собой комплексное число, модуль которого равен отношению амплитуды выходной величины к амплитуде входной, а аргумент – сдвигу фаз выходной величины по отношению к входной. Частотная передаточная функция может быть представлена в следующем виде:
Модуль частотной передаточной функции находится как отношение модулей её числителя и знаменателя.
Правильный ответ: модуль частотной передаточной функции.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 55.
!True
модуль частотной передаточной функции
!False
аргумент частотной передаточной функции
!False
амплитуду и фазу выходного сигнала
!False
амплитуду выходного сигнала
!Task 4
Аналитическое выражение для ФЧХ разомкнутого контура с передаточной функцией
имеет вид …
!Solution
Частотная передаточная функция W(jw) представляет собой комплексное число, модуль которого равен отношению амплитуды выходной величины к амплитуде входной, а аргумент – сдвигу фаз выходной величины по отношению к входной. Частотная передаточная функция может быть представлена в следующем виде:
Аргумент или фаза частотной передаточной функции находиться как разность аргументов числителя и знаменателя. Числитель в данном случае задает нулевой фазовый сдвиг, а знаменатель задает фазовый сдвиг равный сумме сдвигов по фазе от интегратора и апериодического звена.
Правильный ответ:
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 55.
!True
!False
!False
!False
!Task 5
Численное значение амплитудной частотной характеристики звена с передаточной функцией
при частоте =3, равно …
!Solution
Частотная передаточная функция может быть представлена в следующем виде:
Модуль частотной передаточной функции данного звена находится как отношение модулей её числителя и знаменателя:
При =3 значение знаменателя стремится к нулю, а значит A() =∞
Правильный ответ: бесконечности.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия., 2007, 752 с., стр. 55,65.
!True
!False
!False
!False
!Task 6
Выражение для частотной передаточной функции системы, описываемой дифференциальным уравнением
имеет вид …
!Solution
Дифференциальные уравнения записываются так, чтобы выходная величина и её производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. . Считая, условно, оператор дифференцирования p=d/dt алгебраической величиной, решим данное уравнение относительно выходной величины. Получим передаточную функцию. Произведем замену p на jw, получим частотную передаточную функцию.Частотная передаточная функция W(j) представляет собой комплексное число, модуль которого равен отношению амплитуды выходной величины к амплитуде входной, а аргумент – сдвигу фаз выходной величины по отношению к входной. Частотная передаточная функция может быть представлена в следующем виде:
Для нахождения вещественной и мнимой частей частотной передаточной функции необходимо освободиться от мнимости в знаменателе путем умножения числителя и знаменателя на комплексную величину, сопряженную знаменателю, и затем произвести разделение на вещественную и мнимую части.
Правильный ответ:
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб., Профессия. 2007, 752 с., стр. 55-56.
!True
!False
!False
!False
!Task 7
Формула фазового сдвига частотной передаточной функции имеет вид …
!Solution
Частотная передаточная функция W(j) представляет собой комплексное число, модуль которого равен отношению амплитуды выходной величины к амплитуде входной, а аргумент – сдвигу фаз выходной величины по отношению к входной. Частотная передаточная функция может быть представлена в следующем виде:
Аргумент или фаза частотной передаточной функции находиться как разность аргументов числителя и знаменателя или как арктангенс отношения мнимой части к вещественной частотной передаточной функции
Правильный ответ: -
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 55.
!True
!False
!False
!False
!Task 8
Вещественная часть частотной передаточной функции звена
имеет вид …
!Solution
Частотная передаточная функция W(j) представляет собой комплексное число, модуль которого равен отношению амплитуды выходной величины к амплитуде входной, а аргумент – сдвигу фаз выходной величины по отношению к входной. Частотная передаточная функция может быть представлена в следующем виде:
Для нахождения вещественной и мнимой частей частотной передаточной функции необходимо освободиться от мнимости в знаменателе путем умножения числителя и знаменателя на комплексную величину, сопряженную знаменателю, и затем произвести разделение на вещественную и мнимую части.
Правильный ответ:
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб., Профессия. 2007, 752 с., стр. 55-56.
!True
!False
!False
!False
!Task 9
Мнимая часть частотной передаточной функции звена
имеет вид …
Solution
Частотная передаточная функция W(j) представляет собой комплексное число, модуль которого равен отношению амплитуды выходной величины к амплитуде входной, а аргумент – сдвигу фаз выходной величины по отношению к входной. Частотная передаточная функция может быть представлена в следующем виде:
Для нахождения вещественной и мнимой частей частотной передаточной функции необходимо освободиться от мнимости в знаменателе путем умножения числителя и знаменателя на комплексную величину, сопряженную знаменателю, и затем произвести разделение на вещественную и мнимую части.
Правильный ответ:
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб., Профессия. 2007, 752 с., стр. 55-56.
!True
!False
!False
!False
!Task 10
Модуль частотной передаточной функции звена
имеет вид …
!Solution
Частотная передаточная функция W(j) представляет собой комплексное число, модуль которого равен отношению амплитуды выходной величины к амплитуде входной, а аргумент – сдвигу фаз выходной величины по отношению к входной. Частотная передаточная функция может быть представлена в следующем виде:
Модуль частотной передаточной функции находится как отношение модулей её числителя и знаменателя.
Правильный ответ:
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 55.
!True
!False
!False
!False
!Task 11
По осям координат (ось абсцисс и ось ординат) при построении амплитудно-фазовой частотной характеристики откладывают соответственно значения …
!Solution
Амплитудно-фазовая частотная характеристика строится на комплексной плоскости. Она представляет собой геометрическое место концов векторов (годограф), соответствующих частотной передаточной функции
W(j)=U()+jV() при изменении частоты от нуля до бесконечности. По оси абсцисс откладывается вещественная часть U()=Re W(j) и по оси ординат – мнимая часть V()= Im W(j).
Правильный ответ: вещественная и мнимая части частотной передаточной функции звена.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 56.
!True
вещественной и мнимой частей частотной передаточной функции звена
!False
мнимой и вещественной частей частотной передаточной функции звена
!False
модуля и аргумента частотной передаточной функции звена
!False
аргумента и модуля частотной передаточной функции звена
!Task 12
При построении амплитудно-фазовой частотной характеристики в полярных координатах по осям откладываются значения …
!Solution
Амплитудно-фазовая частотная характеристика строится на комплексной плоскости. Она представляет собой геометрическое место концов векторов (годограф), соответствующих частотной передаточной функции. W(j)=U()+jV() при изменении частоты от нуля до бесконечности.
Гораздо проще её строить, используя полярные координаты, т.е. вычисляя непосредственно модуль и фазу. Зная их можно легко построить соответствующую точку на комплексной плоскости.
Правильный ответ: модуля и фазы частотной передаточной функции системы
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 56.
!True
модуля и фазы частотной передаточной функции системы
!False
вещественной и мнимой частей частотной передаточной функции системы
!False
частоты и модуля частотной передаточной функции системы
!False
фазы и частоты выходного сигнала системы
!Task 13
Ошибочной формулой, связывающей модуль частотной передаточной функции (A), фазовый сдвиг (f), вещественную (U) и мнимую (V) части частотной передаточной функции является …
!Solution
Амплитудно-фазовая частотная характеристика строится на комплексной плоскости. Она представляет собой геометрическое место концов векторов (годограф), соответствующих частотной передаточной функции. W(j)=U()+jV() при изменении частоты от нуля до бесконечности.
Гораздо проще её строить, используя полярные координаты, т.е. вычисляя непосредственно модуль и фазу. Зная их можно легко построить соответствующую точку на комплексной плоскости. В случае необходимости при известных модуле и фазе легко вычислить вещественную и мнимую части умножением модуля на направляющий косинус между вектором и соответствующей осью.
Правильный ответ:
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 56.
!True
!False
!False
!False
!Task 14
Ошибочной формулой, связывающей модуль частотной передаточной функции (A), фазовый сдвиг (f), вещественную (U) и мнимую (V) части частотной передаточной функции является …
!Solution
Амплитудно-фазовая частотная характеристика строится на комплексной плоскости. Она представляет собой геометрическое место концов векторов (годограф), соответствующих частотной передаточной функции. W(j)=U()+jV() при изменении частоты от нуля до бесконечности.
Гораздо проще её строить, используя полярные координаты, т.е. вычисляя непосредственно модуль и фазу. Зная их можно легко построить соответствующую точку на комплексной плоскости. В случае необходимости, при известных модуле и фазе легко вычислить вещественную и мнимую части умножением модуля на направляющий косинус между вектором и соответствующей осью.
Правильный ответ:
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 56.
!True
!False
!False
!False
!Task 15
Ошибочной формулой, связывающей модуль частотной передаточной функции (A), фазовый сдвиг (f), вещественную (U) и мнимую (V) части частотной передаточной функции является …
!Solution
Амплитудно-фазовая частотная характеристика строится на комплексной плоскости. Она представляет собой геометрическое место концов векторов (годограф), соответствующих частотной передаточной функции. W(j)=U()+jV() при изменении частоты от нуля до бесконечности.
Гораздо проще её строить, используя полярные координаты, т.е. вычисляя непосредственно модуль и фазу. Зная их можно легко построить соответствующую точку на комплексной плоскости. В случае необходимости при известных модуле и фазе легко вычислить вещественную и мнимую части умножением модуля на направляющий косинус между вектором и соответствующей осью.
Правильный ответ:
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 56.
!True
!False
!False
!False
!Task 16
Амплитудная фазовая частотная характеристика (АФЧХ) при ее определении в диапазоне частот от минус бесконечности до плюс бесконечности симметрична относительно …
!Solution
Амплитудно-фазовая частотная характеристика строится на комплексной плоскости. Она представляет собой геометрическое место концов векторов (годограф), соответствующих частотной передаточной функции. W(j)=U()+jV() при изменении частоты от нуля до бесконечности.
Амплитудная фазовая частотная характеристика (АФЧХ) при ее определении в диапазоне частот от минус бесконечности до плюс бесконечности симметрична относительно оси абсцисс.
Правильный ответ: оси абсцисс.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 55-56.
!True
оси абсцисс
!False
оси ординат
!False
начала координат
!False
точки -1,0
!END
*********************************************
*ОТУ 1.1.04.t2.rtf
*********************************************
!Taskfile ОТУ 1.1.04.#Логарифмические амплитудно- фазо- частотные характеристики
!DE=ОТУ 1.1.#Основные понятия и определения. Математическое описание непрерывных систем
!Type=2
!Time=2
Экспертные и технологические параметры заданий:
1. Дисциплина: Основы теории управления
2. Объем часов: группа I (от 80 до 170 часов)
3. Дидактическая единица ГОС: Основные понятия и определения. Математическое описание непрерывных систем
4. Тема задания: Логарифмические амплитудно- фазо-частотные характеристики
5. Уровень сложности: 2 (знать и уметь использовать в типовой учебной ситуации)
6. Ориентировочное время выполнения: 2 минуты
7. Перечень контролируемых учебных элементов
Студент должен знать: принципы построения логарифмических амплитудно- фазо- частотных характеристик (ЛАФЧХ)
уметь: различать ЛАФЧХ как точные, так и асимптотические
8. Форма заданий: выбор одного ответа из четырех предложенных
!Task 1
Наклон высокочастотной асимптоты ЛАЧХ для системы с уравнением :

составит ______ дБ/дек.
!Solution
Шаг 1- переход от дифференциального уравнения к передаточной функции:
дифференциальные уравнения записываются так, чтобы выходная величина и её производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Считая условно оператор дифференцирования p=d/dt алгебраической величиной, решим данное уравнение относительно выходной величины. Полученное выражение представляет собой символическую запись дифференциального уравнения и вводиться для сокращения её записи. Более строго передаточная функция определяется через изображения Лапласа.
Если
ввести изображения по Лапласу входных
и выходных величин, где s=c+j –
комплексная величина, то передаточную
функцию можно строго определить как
отношение изображений выходной и
входной величины звена при нулевых
начальных условиях и равных нулю
остальных воздействиях на звено.
Передаточная функция будет иметь вид:
–
комплексная величина, то передаточную
функцию можно строго определить как
отношение изображений выходной и
входной величины звена при нулевых
начальных условиях и равных нулю
остальных воздействиях на звено.
Передаточная функция будет иметь вид:
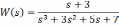
Шаг 2 – построение ЛАЧХ:
При возрастании w строим асимптотическую ЛАХ, как ломанную линию, прямолинейные отрезки которой изменяют наклон при сопрягающих частотах i на ±20 дБ/дек, если i – принадлежит звену первого порядка, ±40 дБ/дек – звену второго порядка и т.д. Здесь «+» соответствует форсирующему звену (числитель ПФ), а «–» - инерционному звену (знаменатель ПФ). В данном случае можно, не определяя значений сопрягающих частот сказать, что максимальный наклон, который дает знаменатель ПФ – -60 дБ/дек , а числитель +20 дБ/дек, какое бы не было расположение сопрягающих частот, высокочастотная часть характеристики будет иметь наклон -40 дБ/дек.
Правильный ответ: -40 дБ/дек.
Литература: 1. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 44-47.
2. Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 88.
!True
-40
!False
0
!False
20
!False
-20
!Task 2
Частотой среза называется …
!Solution
Частота, при которой ЛАЧХ пересекает ось частот, называется частотой среза , т.е. L( )=0.
Правильный ответ: точка пересечения графика ЛАЧХ с осью абсцисс.
Литература: 1. Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 89.
!True
точка пересечения графика ЛАЧХ с осью абсцисс
!False
точка пересечения асимптоты ЛАЧХ с осью абсцисс
!False
точка пересечения графика ЛАЧХ с осью ординат
!False
точка пересечения асимптоты ЛАЧХ с осью ординат
!Task 3
Точка пересечения низкочастотной асимптоты ЛАЧХ с осью ординат соответствует значению …
!Solution
При
построении ЛАЧХ в прямоугольной системе
координат по горизонтальной оси в
логарифмическом масштабе откладываем
сопрягающие частоты, а по вертикальной
оси при
 =1
откладываем 20 lg
K
и проводим через неё низкочастотную
асимптоту.
=1
откладываем 20 lg
K
и проводим через неё низкочастотную
асимптоту.
Правильный ответ: 20lgK.
Литература: 1. Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 88.
!True
20lgK
!False
lgK
!False
частота среза
!False
К
!Task 4
Наклон
ЛАЧХ, соответствующей передаточной
функции вида

на частоте =150[1/c] равен ______ дБ/дек.
!Solution
При возрастании строим асимптотическую ЛАХ, как ломанную линию, прямолинейные отрезки которой изменяют наклон при сопрягающих частотах i на ±20 дБ/дек, если i – принадлежит звену первого порядка, ±40 дБ/дек – звену второго порядка и т.д. Здесь + соответствует форсирующему звену (числитель ПФ ), а – - инерционному звену (знаменатель ПФ). В данном случае низкочастотная часть будет иметь наклон -20 дБ/дек (s – в знаменателе) после частоты 10 1/с наклон буде равен 0 дБ/дек (добавит свои +20 дБ/дек числитель) и после частоты 100 1/с наклон составит -20 дБ/дек. Заданная частота 50 1/с находится в промежутке между сопрягающими частотами 10 и 100 1/с, т.е. наклон на данной частоте будет 0 дБ/дек.
Правильный ответ: -20 дБ/дек.
Литература: 1. Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 88.
!True
-20
!False
0
!False
20
!False
-40
!Task 5
Наклон ЛАЧХ, соответствующей передаточной функции вида:
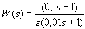
на частоте =50[1/c] равен ______ дБ/дек.
!Solution
При возрастании строим асимптотическую ЛАХ, как ломанную линию, прямолинейные отрезки которой изменяют наклон при сопрягающих частотах i на ±20 дБ/дек, если i – принадлежит звену первого порядка, ±40 дБ/дек – звену второго порядка и т.д. Здесь + соответствует форсирующему звену (числитель ПФ ), а – - инерционному звену (знаменатель ПФ). В данном случае низкочастотная часть будет иметь наклон -20 дБ/дек (s – в знаменателе) после частоты 10 1/с наклон буде равен 0 дБ/дек (добавит свои +20 дБ/дек числитель) и после частоты 100 1/с наклон составит -20 дБ/дек. Заданная частота 50 1/с находится в промежутке между сопрягающими частотами 10 и 100 1/с, т.е. наклон на данной частоте будет 0 дБ/дек.
Правильный ответ: 0 дБ/дек.
Литература: 1. Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 88.
!True
0
!False
-20
!False
20
!False
-40
!Task 6
Наклон ЛАЧХ, соответствующей передаточной функции вида:

на частоте 1.5 1/с равен ______ дБ/дек.
!Solution
При возрастании строим асимптотическую ЛАХ, как ломанную линию, прямолинейные отрезки которой изменяют наклон при сопрягающих частотах i на ±20 дБ/дек, если i – принадлежит звену первого порядка, ±40 дБ/дек – звену второго порядка и т.д. Здесь + соответствует форсирующему звену (числитель ПФ ), а – - инерционному звену (знаменатель ПФ). В данном случае низкочастотная часть будет иметь наклон 0 дБ/дек до сопрягающей частоты 0.25 1/с (постоянная времени 4 с – в знаменателе) после неё наклон составит – 20 дБ/дек , до частоты 1 1/с (постоянная времени 1 с в знаменателе)после данной частоты наклон составит 0 дБ/дек (добавит свои +20 дБ/дек числитель) и после частоты 2 1/с наклон составит -20 дБ/дек (постоянная времени в знаменателе 0,5 с). Заданная частота 1, 5 1/с находится в промежутке между сопрягающими частотами 1 и 2 1/с, т.е. наклон на данной частоте будет 0 дБ/дек
Правильный ответ: 0 дБ/дек.
Литература: 1. Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 88.
!True
0
!False
-20
!False
20
!False
-40
!Task 7
Наклон асимптотической ЛАЧХ на частоте 1.5 1/с системы с передаточной функцией

равен ______ дБ/дек.
!Solution
При возрастании строим асимптотическую ЛАХ, как ломанную линию, прямолинейные отрезки которой изменяют наклон при сопрягающих частотах i на ±20 дБ/дек, если i – принадлежит звену первого порядка, ±40 дБ/дек – звену второго порядка и т.д. Здесь + соответствует форсирующему звену (числитель ПФ ), а – - инерционному звену (знаменатель ПФ).
В данном случае низкочастотная часть будет иметь наклон 0 дБ/дек до сопрягающей частоты 0.2 1/с (постоянная времени 5 с – в знаменателе) после неё наклон составит – 20 дБ/дек , до частоты 1 1/с (постоянная времени 1 с в знаменателе) после данной частоты наклон составит -40 дБ/дек (добавит свои -20 дБ/дек звено с постоянной 1с ). Заданная частота 1, 5 1/с находится правее сопрягающей частоты 1 1/с, т.е. наклон на данной частоте будет -40 дБ/дек.
Правильный ответ: -40 дБ/дек.
Литература: 1. Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 88.
!True
-40
!False
-20
!False
20
!False
0
!Task 8
Наклон асимптотической ЛАЧХ на частоте 1.5 1/с звена с передаточной функцией вида:

равен ______ дБ/дек.
!Solution
При возрастании строим асимптотическую ЛАХ, как ломанную линию, прямолинейные отрезки которой изменяют наклон при сопрягающих частотах i на ±20 дБ/дек, если i – принадлежит звену первого порядка, ±40 дБ/дек – звену второго порядка и т.д. Здесь + соответствует форсирующему ему звену (числитель ПФ ), а – - инерционному звену (знаменатель ПФ). В данном случае низкочастотная часть будет иметь наклон -20 дБ/дек (s – в знаменателе) после частоты 0.25 1/с наклон буде равен -40 дБ/дек (добавит свои -20 дБ/дек звено с постоянной времени 4 с в знаменателе) и после частоты 1 1/с наклон составит -20 дБ/дек (добавит свой наклон +20 дБ/дек звено с постоянной времени 1 с в числителе). Заданная частота 1,5 1/с находится правее частоты 1 1/с, т.е. наклон характеристики на данной частоте будет -20 дБ/дек.
Правильный ответ: -20 дБ/дек.
Литература: 1. Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 88.
!True
-20
!False
20
!False
-40
!False
0
!Task 9
Наклон асимптотической ЛАЧХ на частоте 1.5 1/с звена с передаточной функцией вида:

равен ______ дБ/дек.
!Solution
При возрастании строим асимптотическую ЛАХ, как ломанную линию, прямолинейные отрезки которой изменяют наклон при сопрягающих частотах i на ±20 дБ/дек, если i – принадлежит звену первого порядка, ±40 дБ/дек – звену второго порядка и т.д. Здесь + соответствует форсирующему звену (числитель ПФ ), а – - инерционному звену (знаменатель ПФ). В данном случае низкочастотная часть будет иметь наклон -40 дБ/дек (s2 – в знаменателе) после частоты 0.25 1/с наклон буде равен -60 дБ/дек (добавит свои -20 дБ/дек звено с постоянной времени 4 с в знаменателе) и после частоты 1 1/с наклон составит -40 дБ/дек (добавит свой наклон +20 дБ/дек звено с постоянной времени 1 с в числителе). Заданная частота 1,5 1/с находится правее частоты 1 1/с, т.е. наклон характеристики на данной частоте будет -40 дБ/дек.
Правильный ответ: -40 дБ/дек.
Литература: 1. Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 88.
!True
-40
!False
20
!False
-20
!False
-60
!Task 10
Наклон асимптотической ЛАЧХ на частоте 0.75[ 1/с] звена с передаточной функцией вида:

равен ______ дБ/дек.
!Solution
При возрастании строим асимптотическую ЛАХ, как ломанную линию, прямолинейные отрезки которой изменяют наклон при сопрягающих частотах i на ±20 дБ/дек, если i – принадлежит звену первого порядка, ±40 дБ/дек – звену второго порядка и т.д. Здесь + соответствует форсирующему звену (числитель ПФ ), а – - инерционному звену (знаменатель ПФ). В данном случае низкочастотная часть будет иметь наклон -20 дБ/дек (s – в знаменателе) после частоты 0.25[ 1/с] наклон буде равен 0 дБ/дек (добавит свои +20 дБ/дек звено с постоянной времени 4 с в числителе) и после частоты 1 1/с наклон составит -20 дБ/дек (добавит свой наклон -20 дБ/дек звено с постоянной времени 1 с в знаменателе). Заданная частота 0,75 1/с находится находится в промежутке между сопрягающими частотами 0,25 и 1 1/с, т.е. наклон на данной частоте будет 0 дБ/дек.
Правильный ответ: 0 дБ/дек.
Литература: 1. Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 88.
!True
0
!False
20
!False
-20
!False
-40
!Task 11
Наклон асимптотической ЛАЧХ на частоте 0.5 1/с звена с передаточной функцией вида:

равен ______ дБ/дек.
!Solution
При возрастании строим асимптотическую ЛАХ, как ломанную линию, прямолинейные отрезки которой изменяют наклон при сопрягающих частотах i на ±20 дБ/дек, если i – принадлежит звену первого порядка, ±40 дБ/дек – звену второго порядка и т.д. Здесь + соответствует форсирующему звену (числитель ПФ ), а – - инерционному звену (знаменатель ПФ). В данном случае низкочастотная часть будет иметь наклон 0 дБ/дек до сопрягающей частоты 0.25 1/с (постоянная времени 4 с – в числителе) после неё наклон составит + 20 дБ/дек , до частоты 1 1/с (постоянная времени 1 с в знаменателе)после данной частоты наклон составит 0 дБ/дек (добавит свои - 20 дБ/дек звено с постоянной времени 1 с в знаменателе) . Заданная частота 0, 5 1/с находится в промежутке между сопрягающими частотами 0,25 и 1 1/с, т.е. наклон на данной частоте будет +20 дБ/дек
Правильный ответ: +20 дБ/дек.
Литература: 1. Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 88.
!True
+20
!False
-20
!False
0
!False
-40
!Task 12
Наклон асимптотической ЛАЧХ на частоте 1.5 1/с звена с передаточной функцией вида:

равен ______ дБ/дек.
!Solution
При возрастании строим асимптотическую ЛАХ, как ломанную линию, прямолинейные отрезки которой изменяют наклон при сопрягающих частотах i на ±20 дБ/дек, если i – принадлежит звену первого порядка, ±40 дБ/дек – звену второго порядка и т.д. Здесь + соответствует форсирующему звену (числитель ПФ ), а – - инерционному звену (знаменатель ПФ). В данном случае низкочастотная часть будет иметь наклон -20 дБ/дек (s – в знаменателе) после частоты 1 1/с наклон буде равен 0 дБ/дек (добавит свои +20 дБ/дек числитель) и после частоты 2 1/с наклон составит -20 дБ/дек. Заданная частота 1,5 1/с находится в промежутке между сопрягающими частотами 1 и 2 1/с, т.е. наклон на данной частоте будет 0 дБ/дек.
Правильный ответ: 0 дБ/дек.
Литература: 1. Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 88.
!True
0
!False
20
!False
-20
!False
-40
!Task 13
Наклон асимптотической ЛАЧХ на частоте 1.5 1/с звена с передаточной функцией вида:

равен ______ дБ/дек.
!Solution
При возрастании строим асимптотическую ЛАХ, как ломанную линию, прямолинейные отрезки которой изменяют наклон при сопрягающих частотах i на ±20 дБ/дек, если i – принадлежит звену первого порядка, ±40 дБ/дек – звену второго порядка и т.д. Здесь + соответствует форсирующему звену (числитель ПФ ), а – - инерционному звену (знаменатель ПФ). В данном случае низкочастотная часть будет иметь наклон -20 дБ/дек (s – в знаменателе) после частоты 0,2 1/с наклон буде равен -40 дБ/дек (добавит свои -20 дБ/дек второе звено знаменателя) и после частоты 0,5 1/с наклон составит -20 дБ/дек (звено с постоянной 2 с в числителе) и после частоты 1 1/с наклон станет 0 дБ/дек (ещё +20 дБ/дек добавит второе звено числителя) Заданная частота 1,5 1/с находится правее частоты 1 1/с, т.е. наклон на данной частоте будет 0 дБ/дек.
Правильный ответ: 0 дБ/дек.
Литература: 1. Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 88.
!True
0
!False
20
!False
-20
!False
-40
!Task 14
Наклон асимптотической ЛАЧХ на частоте 25 1/с звена с передаточной функцией вида:

равен ______ дБ/дек.
!Solution
При возрастании строим асимптотическую ЛАХ, как ломанную линию, прямолинейные отрезки которой изменяют наклон при сопрягающих частотах i на ±20 дБ/дек, если i – принадлежит звену первого порядка, ±40 дБ/дек – звену второго порядка и т.д. Здесь + соответствует форсирующему звену (числитель ПФ ), а – - инерционному звену (знаменатель ПФ). В данном случае низкочастотная часть будет иметь наклон 0 дБ/дек до сопрягающей частоты 2,5 1/с, после неё во всём диапазоне частот наклон будет -40 дБ/дек, т.к. имеем двойное апериодическое звено, т.е. наклон на данной частоте составит -40 дБ/дек.
Правильный ответ: -40 дБ/дек.
Литература: 1. Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 88.
!True
-40
!False
0
!False
20
!False
-20
!Task 15
Наклон асимптотической ЛАЧХ на частоте 5 1/с звена с передаточной функцией вида:

равен ______ дБ/дек.
!Solution
При возрастании строим асимптотическую ЛАХ, как ломанную линию, прямолинейные отрезки которой изменяют наклон при сопрягающих частотах i на ±20 дБ/дек, если i – принадлежит звену первого порядка, ±40 дБ/дек – звену второго порядка и т.д. Здесь + соответствует форсирующему звену (числитель ПФ ), а – - инерционному звену (знаменатель ПФ). В данном случае низкочастотная часть будет иметь наклон +20 дБ/дек (s – в числителе) после частоты 2,5 1/с наклон буде равен -20 дБ/дек (добавит свои -40 дБ/дек знаменатель) Заданная частота 5 1/с находится правее самой высокой сопрягающей частоты т.е. наклон на данной частоте будет -20 дБ/дек.
Правильный ответ: -20 дБ/дек.
Литература: 1. Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 88.
!True
-20
!False
20
!False
-40
!False
0
!Task 16
Наклон асимптотической ЛАЧХ на частоте 25 1/с звена с передаточной функцией вида:
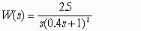
равен ______ дБ/дек.
!Solution
При возрастании строим асимптотическую ЛАХ, как ломанную линию, прямолинейные отрезки которой изменяют наклон при сопрягающих частотах i на ±20 дБ/дек, если i – принадлежит звену первого порядка, ±40 дБ/дек – звену второго порядка и т.д. Здесь + соответствует форсирующему звену (числитель ПФ ), а – - инерционному звену (знаменатель ПФ). В данном случае низкочастотная часть будет иметь наклон -20 дБ/дек (s – в знаменателе) и после частоты 2,5 1/с наклон составит -60 дБ/дек (добавит свои -40 дБ/дек двойное апериодическое звено с постоянной времени 0,4 с. Заданная частота 25 1/с находится правее сопрягающей частоты 2,5 1/с т.е. наклон на данной частоте будет -60 дБ/дек
Правильный ответ: -60 дБ/дек.
Литература: 1. Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 88.
!True
-60
!False
20
!False
-40
!False
0
!Task 17
Передаточная функция звена, имеющего данную ЛАЧХ:

имеет вид …
!Solution
При возрастании строим асимптотическую ЛАХ, как ломанную линию, прямолинейные отрезки которой изменяют наклон при сопрягающих частотах i на ±20 дБ/дек, если i – принадлежит звену первого порядка, ±40 дБ/дек – звену второго порядка и т.д. Здесь + соответствует форсирующему звену (числитель ПФ ), а – - инерционному звену (знаменатель ПФ). В данном случае низкочастотная часть имеет наклон +20 дБ/дек . т.е. s – в числителе, на частоте w=1 наклон становится 0 дБ/дек, это значит что в знаменателе должно быть апериодическое звено.
Правильный
ответ:
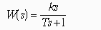
Литература: 1. Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 88.
!True

!False

!False

!False

!Task 18
Передаточная функция звена, имеющего данную ЛАЧХ:

имеет вид …
!Solution
При возрастании строим асимптотическую ЛАХ, как ломанную линию, прямолинейные отрезки которой изменяют наклон при сопрягающих частотах i на ±20 дБ/дек, если i – принадлежит звену первого порядка, ±40 дБ/дек – звену второго порядка и т.д. Здесь + соответствует форсирующему звену (числитель ПФ ), а – - инерционному звену (знаменатель ПФ). В данном случае низкочастотная часть имеет наклон 0 дБ/дек . т.е. s – отсутствует, на частоте w=1 наклон становится -40 дБ/дек, это значит что в знаменателе должно быть апериодическое звено второго порядка (двойное апериодическое звено).
Правильный
ответ:
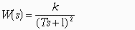
Литература: 1. Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 88.
!True

!False

!False

!False

!Task 19
Первой сопрягающей частотой логарифмической амплитудно-частотной характеристики системы с передаточной функцией вида:

равна ______ 1/с.
!Solution
При возрастании строим асимптотическую ЛАХ, как ломанную линию, прямолинейные отрезки которой изменяют наклон при сопрягающих частотах i на ±20 дБ/дек, если i – принадлежит звену первого порядка, ±40 дБ/дек – звену второго порядка и т.д. Здесь + соответствует форсирующему звену (числитель ПФ ), а – - инерционному звену (знаменатель ПФ). В данном случае первая сопрягающая частота соответствует самой большой постоянной времени (4 с).
Правильный ответ: 0,25 1/с
Литература: 1. Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 88.
!True
0.25
!False
0.1
!False
0.5
!False
1.0
!Task 20
Первая сопрягающая частота логарифмической амплитудно-частотной характеристики системы, описываемой дифференциальным уравнением вида:

равна ______ 1/с.
!Solution
Шаг 1- переход от дифференциального уравнения к передаточной функции:
дифференциальные уравнения записываются так, чтобы выходная величина и её производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Считая условно оператор дифференцирования p=d/dt алгебраической величиной, решим данное уравнение относительно выходной величины. Полученное выражение представляет собой символическую запись дифференциального уравнения и вводиться для сокращения её записи. Более строго передаточная функция определяется через изображения Лапласа.
Если ввести изображения по Лапласу входных и выходных величин, где s=c+j – комплексная величина, то передаточную функцию можно строго определить как отношение изображений выходной и входной величины звена при нулевых начальных условиях и равных нулю остальных воздействиях на звено. Передаточная функция будет иметь вид:

Шаг 2 поиск сопрягающей частоты:
первая сопрягающая частота будет соответствовать постоянной времени 5 с, т.е будет равна 0,2 1/с.
Правильный ответ: 0,2 1/с.
Литература: 1. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 44-47.
!True
0,2
!False
5.0.
!False
0.25
!False
0.5
!Task 21
Логарифмическая фазочастотная характеристика системы с передаточной фукцией вида:

при изменении частоты от 0 до ∞ находится в диапазоне …
!Solution
Логарифмическая фазочастотная характеристика системы определяется как сумма ФЧХ входящих в неё звеньев, причем инерционным звеньям соответствует одна и та же функция частоты : ±arctg T , которая изменяется от 0 до π/2 при изменении частоты от 0 до ∞ (положительные фазовые сдвиги вносят звенья, которые находятся в числителе а отрицательные – в знаменателе). Идеальное интегрирующее звено на всех частотах вносит фазовый сдвиг –π/2, идеальное дифференцирующее звено +π/2. Для того чтобы определить диапазон изменения ФЧХ достаточно найти суммарный фазовый сдвиг при =0 и при ->∞
Правильный ответ: от 0 до -π.
Литература: 1. Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 52.
2. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 145.
!True
от 0 до -π
!False
от 0 до ∞
!False
от –π/2 до π
!False
от 0 до –π/2
!Task 22
Логарифмическая фазочастотная характеристика системы с передаточной фукцией вида:
 ,
,
в крайних точках частотного диапазона (0 и ∞), имеет фазовые сдвиги …
!Solution
Логарифмическая фазочастотная характеристика системы определяется как сумма ФЧХ входящих в неё звеньев, причем инерционным звеньям соответствует одна и та же функция частоты : ±arctg T , которая изменяется от 0 до π/2 при изменении частоты от 0 до ∞ (положительные фазовые сдвиги вносят звенья, которые находятся в числителе а отрицательные – в знаменателе). Идеальное интегрирующее звено на всех частотах вносит фазовый сдвиг –π/2, идеальное дифференцирующее звено +π/2. Для того чтобы определить диапазон изменения ФЧХ достаточно найти суммарный фазовый сдвиг при =0 и при ->∞
Правильный ответ: –π/2 и –π/2
Литература: 1. Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 52.
2. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 145.
!True
–π/2 и –π/2
!False
0 и ∞
!False
–π/2 и -π
!False
0 и –π/2
!END
*********************************************
*ОТУ 1.2.01.t5.rtf
*********************************************
!Taskfile ОТУ 1.2.01.#Типовые динамические звенья и их математическое описание
!DE=ОТУ 1.2.# Структурные представления систем управления
!Type=5
!Time=2
Экспертные и технологические параметры заданий:
1. Дисциплина: Основы теории управления
2. Объем часов: группа I (от 80 до 170 часов)
3. Дидактическая единица ГОС: Структурные представления систем управления
4. Тема задания: Типовые динамические звенья и их математическое описание
5. Уровень сложности: 2 (знать и уметь использовать в типовой учебной ситуации)
6. Ориентировочное время выполнения: 2 минуты
7. Перечень контролируемых учебных элементов
Студент должен знать: принципы разбиения на типовые динамические звенья
уметь: раскладывать передаточные функции(ПФ) систем на ПФ типовых звеньев
8. Форма заданий: задания на установление соответствия
!Task 1
Установите соответствие между видом дифференциального уравнения и названием типового динамического звена
1.
2.

3.

4.


!Solution
Дифференциальные уравнения записываются так, чтобы выходная величина и её производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Считая условно оператор дифференцирования p=d/dt алгебраической величиной, решим данное уравнение относительно выходной величины. Полученное выражение представляет собой символическую запись дифференциального уравнения и вводиться для сокращения её записи. Более строго передаточная функция определяется через изображения Лапласа.
Если ввести изображения по Лапласу входных и выходных величин, где s=c+jw – комплексная величина, то передаточную функцию можно строго определить как отношение изображений выходной и входной величины звена при нулевых начальных условиях и равных нулю остальных воздействиях на звено.
Правильное соответствие:
апериодическое звено первого порядка
апериодическое звено второго порядка
консервативное звено
дифференцирующее звено
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 44-47.
!True
апериодическое звено первого порядка
!True
апериодическое звено второго порядка
!True
консервативное звено
!True
дифференцирующее звено
!Task 2
Установите соответствие между видом дифференциального уравнения и названием типового динамического звена
1.
2.

3.

4.


!Solution
Дифференциальные уравнения записываются так, чтобы выходная величина и её производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Считая условно оператор дифференцирования p=d/dt алгебраической величиной, решим данное уравнение относительно выходной величины. Полученное выражение представляет собой символическую запись дифференциального уравнения и вводиться для сокращения её записи. Более строго передаточная функция определяется через изображения Лапласа.
Если ввести изображения по Лапласу входных и выходных величин, где s=c+jw – комплексная величина, то передаточную функцию можно строго определить как отношение изображений выходной и входной величины звена при нулевых начальных условиях и равных нулю остальных воздействиях на звено.
Правильное соответствие:
апериодическое звено первого порядка.
апериодическое звено второго порядка.
консервативное звено.
интегрирующее звено.
!False
дифференцирующее звено
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 44-47.
!True
апериодическое звено первого порядка
!True
апериодическое звено второго порядка
!True
консервативное звено
!True
интегрирующее звено
!Task 3
Установите соответствие между видом дифференциального уравнения и названием типового динамического звена
1.

2.

3.

4.

!Solution
Дифференциальные уравнения записываются так, чтобы выходная величина и её производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Считая условно оператор дифференцирования p=d/dt алгебраической величиной, решим данное уравнение относительно выходной величины. Полученное выражение представляет собой символическую запись дифференциального уравнения и вводиться для сокращения её записи. Более строго передаточная функция определяется через изображения Лапласа.
Если ввести изображения по Лапласу входных и выходных величин, где s=c+jw – комплексная величина, то передаточную функцию можно строго определить как отношение изображений выходной и входной величины звена при нулевых начальных условиях и равных нулю остальных воздействиях на звено.
Правильное соответствие:
апериодическое звено первого порядка.
реальное дифференцирующее звено.
дифференцирующее звено.
интегрирующее звено
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 44-47.
!True
апериодическое звено первого порядка
!True
реальное дифференцирующее звено
!True
дифференцирующее звено
!True
интегрирующее звено
!Task 4
Установите соответствие между видом дифференциального уравнения и названием типового динамического звена
1.

2.

3.

4.

!Solution
Дифференциальные уравнения записываются так, чтобы выходная величина и её производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Считая условно оператор дифференцирования p=d/dt алгебраической величиной, решим данное уравнение относительно выходной величины. Полученное выражение представляет собой символическую запись дифференциального уравнения и вводиться для сокращения её записи. Более строго передаточная функция определяется через изображения Лапласа.
Если ввести изображения по Лапласу входных и выходных величин, где s=c+jw – комплексная величина, то передаточную функцию можно строго определить как отношение изображений выходной и входной величины звена при нулевых начальных условиях и равных нулю остальных воздействиях на звено.
Правильное соответствие:
апериодическое звено первого порядка.
изодром.
дифференцирующее звено.
интегрирующее звено.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 44-47.
!True
апериодическое звено первого порядка
!True
изодром.
!True
дифференцирующее звено
!True
интегрирующее звено
!Task 5
Установите соответствие между видом дифференциального уравнения и названием типового динамического звена
1.

2.

3.

4.

!Solution
Дифференциальные уравнения записываются так, чтобы выходная величина и её производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Считая условно оператор дифференцирования p=d/dt алгебраической величиной, решим данное уравнение относительно выходной величины. Полученное выражение представляет собой символическую запись дифференциального уравнения и вводиться для сокращения её записи. Более строго передаточная функция определяется через изображения Лапласа.
Если ввести изображения по Лапласу входных и выходных величин, где s=c+jw – комплексная величина, то передаточную функцию можно строго определить как отношение изображений выходной и входной величины звена при нулевых начальных условиях и равных нулю остальных воздействиях на звено.
Правильное соответствие:
апериодическое звено первого порядка.
изодром.
реальное дифференцирующее звено.
консервативное звено.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 44-47.
!True
апериодическое звено первого порядка
!True
изодром.
!True
реальное дифференцирующее звено
!True
консервативное звено
!Task 6
Установите соответствие между видом дифференциального уравнения и названием типового динамического звена
1.

2.

3.

4.

!Solution
Дифференциальные уравнения записываются так, чтобы выходная величина и её производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Считая условно оператор дифференцирования p=d/dt алгебраической величиной, решим данное уравнение относительно выходной величины. Полученное выражение представляет собой символическую запись дифференциального уравнения и вводиться для сокращения её записи. Более строго передаточная функция определяется через изображения Лапласа.
Если ввести изображения по Лапласу входных и выходных величин, где s=c+jw – комплексная величина, то передаточную функцию можно строго определить как отношение изображений выходной и входной величины звена при нулевых начальных условиях и равных нулю остальных воздействиях на звено.
Правильное соответствие:
апериодическое звено первого порядка.
колебательное звено второго порядка.
апериодическое звено второго порядка.
консервативное звено.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 44-47.
!True
апериодическое звено первого порядка
!True
колебательное звено второго порядка
!True
апериодическое звено второго порядка
!True
консервативное звено
!Task 7
Установите соответствие между видом дифференциального уравнения и названием типового динамического звена
1.

2.

3.

4.

!Solution
Дифференциальные уравнения записываются так, чтобы выходная величина и её производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Считая условно оператор дифференцирования p=d/dt алгебраической величиной, решим данное уравнение относительно выходной величины. Полученное выражение представляет собой символическую запись дифференциального уравнения и вводиться для сокращения её записи. Более строго передаточная функция определяется через изображения Лапласа.
Если ввести изображения по Лапласу входных и выходных величин, где s=c+jw – комплексная величина, то передаточную функцию можно строго определить как отношение изображений выходной и входной величины звена при нулевых начальных условиях и равных нулю остальных воздействиях на звено.
Правильное соответствие:
реальное дифференцирующее звено.
колебательное звено второго порядка.
консервативное звено.
дифференцирующее звено
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 44-47.
!True
реальное дифференцирующее звено
!True
колебательное звено второго порядка
!True
консервативное звено
!True
дифференцирующее звено
!Task 8
Установите соответствие между видом дифференциального уравнения и названием типового динамического звена
1.

2.

3.

4.

!Solution
Дифференциальные уравнения записываются так, чтобы выходная величина и её производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Считая условно оператор дифференцирования p=d/dt алгебраической величиной, решим данное уравнение относительно выходной величины. Полученное выражение представляет собой символическую запись дифференциального уравнения и вводиться для сокращения её записи. Более строго передаточная функция определяется через изображения Лапласа.
Если ввести изображения по Лапласу входных и выходных величин, где s=c+jw – комплексная величина, то передаточную функцию можно строго определить как отношение изображений выходной и входной величины звена при нулевых начальных условиях и равных нулю остальных воздействиях на звено.
Правильное соответствие:
изодром.
реальное дифференцирующее звено.
дифференцирующее звено
интегрирующее звено.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 44-47.
!True
изодром.
!True
реальное дифференцирующее звено
!True
дифференцирующее звено
!True
интегрирующее звено
!Task 9
Установите соответствие между видом дифференциального уравнения и названием типового динамического звена
1.

2.

3.

4.

!Solution
Дифференциальные уравнения записываются так, чтобы выходная величина и её производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Считая условно оператор дифференцирования p=d/dt алгебраической величиной, решим данное уравнение относительно выходной величины. Полученное выражение представляет собой символическую запись дифференциального уравнения и вводиться для сокращения её записи. Более строго передаточная функция определяется через изображения Лапласа.
Если ввести изображения по Лапласу входных и выходных величин, где s=c+jw – комплексная величина, то передаточную функцию можно строго определить как отношение изображений выходной и входной величины звена при нулевых начальных условиях и равных нулю остальных воздействиях на звено.
Правильное соответствие:
апериодическое звено первого порядка.
колебательное звено второго порядка
консервативное звено.
интегрирующее звено.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 44-47.
!True
апериодическое звено первого порядка
!True
колебательное звено второго порядка
!True
консервативное звено
!True
интегрирующее звено
!Task 10
Установите соответствие между видом дифференциального уравнения и названием типового динамического звена
1.

2.

3.

4.

!Solution
Дифференциальные уравнения записываются так, чтобы выходная величина и её производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Считая условно оператор дифференцирования p=d/dt алгебраической величиной, решим данное уравнение относительно выходной величины. Полученное выражение представляет собой символическую запись дифференциального уравнения и вводиться для сокращения её записи. Более строго передаточная функция определяется через изображения Лапласа.
Если ввести изображения по Лапласу входных и выходных величин, где s=c+jw – комплексная величина, то передаточную функцию можно строго определить как отношение изображений выходной и входной величины звена при нулевых начальных условиях и равных нулю остальных воздействиях на звено.
Правильное соответствие:
консервативное звено.
апериодическое звено второго порядка.
колебательное звено второго порядка.
реальное дифференцирующее звено.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 44-47.
!True
консервативное звено
!True
апериодическое звено второго порядка
!True
колебательное звено второго порядка
!True
реальное дифференцирующее звено
!Task 11
Установите соответствие между видом передаточной функции и названием типового динамического звена
1.

2.
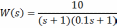
3.

4.

!Solution
Дифференциальные уравнения записываются так, чтобы выходная величина и её производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Считая условно оператор дифференцирования p=d/dt алгебраической величиной, решим данное уравнение относительно выходной величины. Полученное выражение представляет собой символическую запись дифференциального уравнения и вводиться для сокращения её записи. Более строго передаточная функция определяется через изображения Лапласа.
Если ввести изображения по Лапласу входных и выходных величин, где s=c+jw – комплексная величина, то передаточную функцию можно строго определить как отношение изображений выходной и входной величины звена при нулевых начальных условиях и равных нулю остальных воздействиях на звено.
Правильное соответствие:
апериодическое звено первого порядка.
апериодическое звено второго порядка.
консервативное звено.
дифференцирующее звено.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 44-47, 62-65,75,76.
!True
апериодическое звено первого порядка
!True
апериодическое звено второго порядка
!True
консервативное звено
!True
дифференцирующее звено
!Task 12
Установите соответствие между видом передаточной функции и названием типового динамического звена
1.
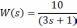
2.

3.

4.
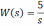
!Solution
Дифференциальные уравнения записываются так, чтобы выходная величина и её производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Считая условно оператор дифференцирования p=d/dt алгебраической величиной, решим данное уравнение относительно выходной величины. Полученное выражение представляет собой символическую запись дифференциального уравнения и вводиться для сокращения её записи. Более строго передаточная функция определяется через изображения Лапласа.
Если ввести изображения по Лапласу входных и выходных величин, где s=c+jw – комплексная величина, то передаточную функцию можно строго определить как отношение изображений выходной и входной величины звена при нулевых начальных условиях и равных нулю остальных воздействиях на звено.
Правильное соответствие:
апериодическое звено первого порядка.
апериодическое звено второго порядка.
консервативное звено.
интегрирующее звено.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 44-47, 62-65,75,76.
!True
апериодическое звено первого порядка
!True
апериодическое звено второго порядка
!True
консервативное звено
!True
интегрирующее звено
!Task 13
Установите соответствие между видом передаточной функции и названием типового динамического звена
1.

2.
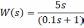
3.
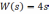
4.
!Solution
Дифференциальные уравнения записываются так, чтобы выходная величина и её производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Считая условно оператор дифференцирования p=d/dt алгебраической величиной, решим данное уравнение относительно выходной величины. Полученное выражение представляет собой символическую запись дифференциального уравнения и вводиться для сокращения её записи. Более строго передаточная функция определяется через изображения Лапласа.
Если ввести изображения по Лапласу входных и выходных величин, где s=c+jw – комплексная величина, то передаточную функцию можно строго определить как отношение изображений выходной и входной величины звена при нулевых начальных условиях и равных нулю остальных воздействиях на звено.
Правильное соответствие:
апериодическое звено первого порядка.
реальное дифференцирующее звено.
дифференцирующее звено.
интегрирующее звено
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 44-47, 62-65,75,76.
!True
апериодическое звено первого порядка
!True
реальное дифференцирующее звено
!True
дифференцирующее звено
!True
интегрирующее звено
!Task 14
Установите соответствие между видом передаточной функции и названием типового динамического звена
1.

2.

3.
4.

!Solution
Дифференциальные уравнения записываются так, чтобы выходная величина и её производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Считая условно оператор дифференцирования p=d/dt алгебраической величиной, решим данное уравнение относительно выходной величины. Полученное выражение представляет собой символическую запись дифференциального уравнения и вводиться для сокращения её записи. Более строго передаточная функция определяется через изображения Лапласа.
Если ввести изображения по Лапласу входных и выходных величин, где s=c+jw – комплексная величина, то передаточную функцию можно строго определить как отношение изображений выходной и входной величины звена при нулевых начальных условиях и равных нулю остальных воздействиях на звено.
Правильное соответствие:
апериодическое звено первого порядка.
изодром.
дифференцирующее звено.
интегрирующее звено.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 44-47, 62-65,75,76.
!True
апериодическое звено первого порядка
!True
изодром
!True
дифференцирующее звено
!True
интегрирующее звено
!Task 15
Установите соответствие между видом передаточной функции и названием типового динамического звена
1.
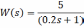
2.

3.
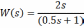
4.

!Solution
Дифференциальные уравнения записываются так, чтобы выходная величина и её производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Считая условно оператор дифференцирования p=d/dt алгебраической величиной, решим данное уравнение относительно выходной величины. Полученное выражение представляет собой символическую запись дифференциального уравнения и вводиться для сокращения её записи. Более строго передаточная функция определяется через изображения Лапласа.
Если ввести изображения по Лапласу входных и выходных величин, где s=c+jw – комплексная величина, то передаточную функцию можно строго определить как отношение изображений выходной и входной величины звена при нулевых начальных условиях и равных нулю остальных воздействиях на звено.
Правильное соответствие:
апериодическое звено первого порядка.
изодром.
реальное дифференцирующее звено.
консервативное звено.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 44-47, 62-65,75,76.
!True
апериодическое звено первого порядка
!True
изодром
!True
реальное дифференцирующее звено
!True
консервативное звено
!Task 16
Установите соответствие между видом передаточной функции и названием типового динамического звена
1.
2.

3.

4.
!Solution
Дифференциальные уравнения записываются так, чтобы выходная величина и её производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Считая условно оператор дифференцирования p=d/dt алгебраической величиной, решим данное уравнение относительно выходной величины. Полученное выражение представляет собой символическую запись дифференциального уравнения и вводиться для сокращения её записи. Более строго передаточная функция определяется через изображения Лапласа.
Если ввести изображения по Лапласу входных и выходных величин, где s=c+jw – комплексная величина, то передаточную функцию можно строго определить как отношение изображений выходной и входной величины звена при нулевых начальных условиях и равных нулю остальных воздействиях на звено.
Правильное соответствие:
апериодическое звено первого порядка.
колебательное звено второго порядка.
апериодическое звено второго порядка.
консервативное звено.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 44-47, 62-65,75,76.
!True
апериодическое звено первого порядка
!True
колебательное звено второго порядка
!True
апериодическое звено второго порядка
!True
консервативное звено
!Task 17
Установите соответствие между видом передаточной функции и названием типового динамического звена
1.

2.

3.

4.
!Solution
Дифференциальные уравнения записываются так, чтобы выходная величина и её производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Считая условно оператор дифференцирования p=d/dt алгебраической величиной, решим данное уравнение относительно выходной величины. Полученное выражение представляет собой символическую запись дифференциального уравнения и вводиться для сокращения её записи. Более строго передаточная функция определяется через изображения Лапласа.
Если ввести изображения по Лапласу входных и выходных величин, где s=c+jw – комплексная величина, то передаточную функцию можно строго определить как отношение изображений выходной и входной величины звена при нулевых начальных условиях и равных нулю остальных воздействиях на звено.
Правильное соответствие:
реальное дифференцирующее звено.
колебательное звено второго порядка.
консервативное звено.
дифференцирующее звено
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 44-47, 62-65,75,76.
!True
реальное дифференцирующее звено
!True
колебательное звено второго порядка
!True
консервативное звено
!True
дифференцирующее звено
!Task 18
Установите соответствие между видом передаточной функции и названием типового динамического звена
1.
2.

3.

4.
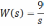
!Solution
Дифференциальные уравнения записываются так, чтобы выходная величина и её производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Считая условно оператор дифференцирования p=d/dt алгебраической величиной, решим данное уравнение относительно выходной величины. Полученное выражение представляет собой символическую запись дифференциального уравнения и вводиться для сокращения её записи. Более строго передаточная функция определяется через изображения Лапласа.
Если ввести изображения по Лапласу входных и выходных величин, где s=c+jw – комплексная величина, то передаточную функцию можно строго определить как отношение изображений выходной и входной величины звена при нулевых начальных условиях и равных нулю остальных воздействиях на звено.
Правильное соответствие:
изодром.
реальное дифференцирующее звено.
дифференцирующее звено.
интегрирующее звено.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 44-47, 62-65,75,76.
!True
изодром
!True
реальное дифференцирующее звено
!True
дифференцирующее звено
!True
интегрирующее звено
!Task 19
Установите соответствие между видом передаточной функции и названием типового динамического звена
1.
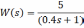
2.

3.

4.
!Solution
Дифференциальные уравнения записываются так, чтобы выходная величина и её производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Считая условно оператор дифференцирования p=d/dt алгебраической величиной, решим данное уравнение относительно выходной величины. Полученное выражение представляет собой символическую запись дифференциального уравнения и вводиться для сокращения её записи. Более строго передаточная функция определяется через изображения Лапласа.
Если ввести изображения по Лапласу входных и выходных величин, где s=c+jw – комплексная величина, то передаточную функцию можно строго определить как отношение изображений выходной и входной величины звена при нулевых начальных условиях и равных нулю остальных воздействиях на звено.
Правильное соответствие:
апериодическое звено первого порядка.
колебательное звено второго порядка
консервативное звено.
интегрирующее звено.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 44-47, 62-65,75,76.
!True
апериодическое звено первого порядка
!True
колебательное звено второго порядка
!True
консервативное звено
!True
интегрирующее звено
!Task 20
Установите соответствие между видом передаточной функции и названием типового динамического звена
1.
2.

3.

4.

!Solution
Дифференциальные уравнения записываются так, чтобы выходная величина и её производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Считая условно оператор дифференцирования p=d/dt алгебраической величиной, решим данное уравнение относительно выходной величины. Полученное выражение представляет собой символическую запись дифференциального уравнения и вводиться для сокращения её записи. Более строго передаточная функция определяется через изображения Лапласа.
Если ввести изображения по Лапласу входных и выходных величин, где s=c+jw – комплексная величина, то передаточную функцию можно строго определить как отношение изображений выходной и входной величины звена при нулевых начальных условиях и равных нулю остальных воздействиях на звено.
Правильное соответствие:
консервативное звено.
апериодическое звено второго порядка.
колебательное звено второго порядка
реальное дифференцирующее звено.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 44-47, 62-65,75,76.
!True
консервативное звено
!True
апериодическое звено второго порядка
!True
колебательное звено второго порядка
!True
реальное дифференцирующее звено
!Task 21
Установите соответствие между названием типового динамического звена и наклоном (наклонами) асимптотической ЛАХ
1. апериодическое звено первого порядка
2. апериодическое звено второго порядка
3. консервативное звено
4. дифференцирующее звено
!Solution
При возрастании w строим асимптотическую ЛАХ, как ломанную линию, прямолинейные отрезки которой изменяют наклон при сопрягающих частотах wi на ±20 дБ/дек, если wi – принадлежит звену первого порядка, ±40 дБ/дек – звену второго порядка и т.д. Здесь + соответствует форсирующему звену (числитель ПФ ), а – - инерционному звену (знаменатель ПФ). В данном случае низкочастотная часть имеет наклон 0 дБ/дек . т.е. s – отсутствует, на частоте w=1 наклон становится -40 дБ/дек, это значит что в знаменателе должно быть апериодическое звено второго порядка (двойное апериодическое звено).
Правильное соответствие:
0 и -20 дБ/дек
0 , -20,-40 дБ/дек
0 ,-40 дБ/дек
+20 дБ/дек
Литература: 1. Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 88
!True
0 и -20 дБ/дек
!True
0 , -20,-40 дБ/дек
!True
0 ,-40 дБ/дек
!True
+20 дБ/дек
!Task 22
Установите соответствие между названием типового динамического звена и наклоном (наклонами) асимптотической ЛАХ
1. апериодическое звено первого порядка
2. консервативное звено
3. интегрирующее звено
4. дифференцирующее звено
!Solution
При возрастании w строим асимптотическую ЛАХ, как ломанную линию, прямолинейные отрезки которой изменяют наклон при сопрягающих частотах wi на ±20 дБ/дек, если wi – принадлежит звену первого порядка, ±40 дБ/дек – звену второго порядка и т.д. Здесь + соответствует форсирующему звену (числитель ПФ ), а – - инерционному звену (знаменатель ПФ). В данном случае низкочастотная часть имеет наклон 0 дБ/дек . т.е. s – отсутствует, на частоте w=1 наклон становится -40 дБ/дек, это значит что в знаменателе должно быть апериодическое звено второго порядка (двойное апериодическое звено).
Правильное соответствие:
0 и -20 дБ/дек
0 ,-40 дБ/дек
-20 дБ/дек
+20 дБ/дек
Литература: 1. Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 88
!True
0 и -20 дБ/дек
!True
0 ,-40 дБ/дек
!True
-20 дБ/дек
!True
+20 дБ/дек
!Task 23
Установите соответствие между названием типового динамического звена и наклоном (наклонами) асимптотической ЛАХ
1. апериодическое звено первого порядка
2. реальное дифференцирующее звено
3. дифференцирующее звено
4. интегрирующее звено
!Solution
При возрастании w строим асимптотическую ЛАХ, как ломанную линию, прямолинейные отрезки которой изменяют наклон при сопрягающих частотах wi на ±20 дБ/дек, если wi – принадлежит звену первого порядка, ±40 дБ/дек – звену второго порядка и т.д. Здесь + соответствует форсирующему звену (числитель ПФ ), а – - инерционному звену (знаменатель ПФ). В данном случае низкочастотная часть имеет наклон 0 дБ/дек . т.е. s – отсутствует, на частоте w=1 наклон становится -40 дБ/дек, это значит что в знаменателе должно быть апериодическое звено второго порядка (двойное апериодическое звено).
Правильное соответствие:
0 и -20 дБ/дек
+20 и 0 дБ/дек
+20 дБ/дек
-20 дБ/дек
Литература: 1. Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 88
!True
0 и -20 дБ/дек
!True
+20 и 0 дБ/дек
!True
+20 дБ/дек
!True
-20 дБ/дек
!Task 24
Установите соответствие между названием типового динамического звена и наклоном (наклонами) асимптотической ЛАХ
1. дифференцирующее звено
2. апериодическое звено первого порядка
3. изодром
4. интегрирующее звено
!Solution
При возрастании w строим асимптотическую ЛАХ, как ломанную линию, прямолинейные отрезки которой изменяют наклон при сопрягающих частотах wi на ±20 дБ/дек, если wi – принадлежит звену первого порядка, ±40 дБ/дек – звену второго порядка и т.д. Здесь + соответствует форсирующему звену (числитель ПФ ), а – - инерционному звену (знаменатель ПФ). В данном случае низкочастотная часть имеет наклон 0 дБ/дек . т.е. s – отсутствует, на частоте w=1 наклон становится -40 дБ/дек, это значит что в знаменателе должно быть апериодическое звено второго порядка (двойное апериодическое звено).
Правильное соответствие:
+20 дБ/дек
0 и -20 дБ/дек
-20 и 0 дБ/дек
-20 дБ/дек
Литература: 1. Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 88
!True
+20 дБ/дек
!True
0 и -20 дБ/дек
!True
-20 и 0 дБ/дек
!True
-20 дБ/дек
!Task 25
Установите соответствие между названием типового динамического звена и наклоном (наклонами) асимптотической ЛАХ
1. апериодическое звено второго порядка
2. изодром
3. реальное дифференцирующее звено
4. консервативное звено
!Solution
При возрастании w строим асимптотическую ЛАХ, как ломанную линию, прямолинейные отрезки которой изменяют наклон при сопрягающих частотах wi на ±20 дБ/дек, если wi – принадлежит звену первого порядка, ±40 дБ/дек – звену второго порядка и т.д. Здесь + соответствует форсирующему звену (числитель ПФ ), а – - инерционному звену (знаменатель ПФ). В данном случае низкочастотная часть имеет наклон 0 дБ/дек . т.е. s – отсутствует, на частоте w=1 наклон становится -40 дБ/дек, это значит что в знаменателе должно быть апериодическое звено второго порядка (двойное апериодическое звено).
Правильное соответствие:
0 , -20,-40 дБ/дек
-20 и 0 дБ/дек
+20 и 0 дБ/дек
0 , -40 дБ/дек
Литература: 1. Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 88
!True
0 , -20,-40 дБ/дек
!True
-20 и 0 дБ/дек
!True
+20 и 0 дБ/дек
!True
0 ,-40 дБ/дек
!Task 26
Установите соответствие между названием типового динамического звена и наклоном (наклонами) асимптотической ЛАХ
1. интегрирующее звено с замедлением.
2. колебательное звено второго порядка.
3. апериодическое звено второго порядка.
4. консервативное звено.
!Solution
При возрастании w строим асимптотическую ЛАХ, как ломанную линию, прямолинейные отрезки которой изменяют наклон при сопрягающих частотах wi на ±20 дБ/дек, если wi – принадлежит звену первого порядка, ±40 дБ/дек – звену второго порядка и т.д. Здесь + соответствует форсирующему звену (числитель ПФ ), а – - инерционному звену (знаменатель ПФ). В данном случае низкочастотная часть имеет наклон 0 дБ/дек . т.е. s – отсутствует, на частоте w=1 наклон становится -40 дБ/дек, это значит что в знаменателе должно быть апериодическое звено второго порядка (двойное апериодическое звено).
Правильное соответствие:
-20 и -40 дБ/дек
0 и -40 дБ/дек
0, -20, -40 дБ/дек
0, -40 дБ/дек
Литература: 1. Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 88
!True
-20 и -40 дБ/дек
!True
0 и -40 дБ/дек
!True
0, -20, -40 дБ/дек
!True
0, -40 дБ/дек
!Task 27
Установите соответствие между названием типового динамического звена и наклоном (наклонами) асимптотической ЛАХ
1. реальное дифференцирующее звено
2. колебательное звено второго порядка
3. интегрирующее звено с замедлением
4. дифференцирующее звено
!Solution
При возрастании w строим асимптотическую ЛАХ, как ломанную линию, прямолинейные отрезки которой изменяют наклон при сопрягающих частотах wi на ±20 дБ/дек, если wi – принадлежит звену первого порядка, ±40 дБ/дек – звену второго порядка и т.д. Здесь + соответствует форсирующему звену (числитель ПФ ), а – - инерционному звену (знаменатель ПФ). В данном случае низкочастотная часть имеет наклон 0 дБ/дек . т.е. s – отсутствует, на частоте w=1 наклон становится -40 дБ/дек, это значит что в знаменателе должно быть апериодическое звено второго порядка (двойное апериодическое звено).
Правильное соответствие:
+20 и 0 дБ/дек
0 и -40 дБ/дек
-20 и -40 дБ/дек
+20 дБ/дек
Литература: 1. Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 88
!True
+20 и 0 дБ/дек
!True
0 и -40 дБ/дек
!True
-20 и -40 дБ/дек
!True
+20 дБ/дек
!Task 28
Установите соответствие между названием типового динамического звена и наклоном (наклонами) асимптотической ЛАХ
1. изодром 2. реальное дифференцирующее звено 3. дифференцирующее звено
4. интегрирующее звено
!Solution
При возрастании w строим асимптотическую ЛАХ, как ломанную линию, прямолинейные отрезки которой изменяют наклон при сопрягающих частотах wi на ±20 дБ/дек, если wi – принадлежит звену первого порядка, ±40 дБ/дек – звену второго порядка и т.д. Здесь + соответствует форсирующему звену (числитель ПФ ), а – - инерционному звену (знаменатель ПФ). В данном случае низкочастотная часть имеет наклон 0 дБ/дек . т.е. s – отсутствует, на частоте w=1 наклон становится -40 дБ/дек, это значит что в знаменателе должно быть апериодическое звено второго порядка (двойное апериодическое звено).
Правильное соответствие:
-20 и 0 дБ/дек
+20 и 0 дБ/дек
+20 дБ/дек
-20 дБ/дек
Литература: 1. Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 88
!True
-20 и 0 дБ/дек
!True
+20 и 0 дБ/дек
!True
+20 дБ/дек
!True
-20 дБ/дек
!Task 29
Установите соответствие между названием типового динамического звена и наклоном (наклонами) асимптотической ЛАХ
1. апериодическое звено первого порядка
2. колебательное звено второго порядка
3. дифференцирующее звено
4. интегрирующее звено с замедлением
!Solution
При возрастании w строим асимптотическую ЛАХ, как ломанную линию, прямолинейные отрезки которой изменяют наклон при сопрягающих частотах wi на ±20 дБ/дек, если wi – принадлежит звену первого порядка, ±40 дБ/дек – звену второго порядка и т.д. Здесь + соответствует форсирующему звену (числитель ПФ ), а – - инерционному звену (знаменатель ПФ). В данном случае низкочастотная часть имеет наклон 0 дБ/дек . т.е. s – отсутствует, на частоте w=1 наклон становится -40 дБ/дек, это значит что в знаменателе должно быть апериодическое звено второго порядка (двойное апериодическое звено).
Правильное соответствие:
0 и -20 дБ/дек
0 и -40 дБ/дек
+20 дБ/дек
-20 и -40 дБ/дек
Литература: 1. Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 88
!True
0 и -20 дБ/дек
!True
0 и -40 дБ/дек
!True
+20 дБ/дек
!True
-20 и -40 дБ/дек
!Task 30
Установите соответствие между названием типового динамического звена и наклоном (наклонами) асимптотической ЛАХ
1. консервативное звено
2. апериодическое звено второго порядка
3. интегрирующее звено
4. реальное дифференцирующее звено
!Solution
При возрастании w строим асимптотическую ЛАХ, как ломанную линию, прямолинейные отрезки которой изменяют наклон при сопрягающих частотах wi на ±20 дБ/дек, если wi – принадлежит звену первого порядка, ±40 дБ/дек – звену второго порядка и т.д. Здесь + соответствует форсирующему звену (числитель ПФ ), а – - инерционному звену (знаменатель ПФ). В данном случае низкочастотная часть имеет наклон 0 дБ/дек . т.е. s – отсутствует, на частоте w=1 наклон становится -40 дБ/дек, это значит что в знаменателе должно быть апериодическое звено второго порядка (двойное апериодическое звено).
Правильное соответствие:
0 и -40 дБ/дек
0, -20, -40 дБ/дек
-20 дБ/дек
+20 и 0 дБ/дек
Литература: 1. Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 88
!True
0 и -40 дБ/дек
!True
0, -20, -40 дБ/дек
!True
-20 дБ/дек
!True
+20 и 0 дБ/дек
!Task 31
Установите соответствие между названием типового динамического звена и
максимального значения вносимого им фазового сдвига
1. апериодическое звено первого порядка.
2. безынерционное звено
3. апериодическое звено первого порядка.
4. дифференцирующее звено.
!Solution
Фазовой характеристике инерционных звеньев соответствует одна и та же функция частоты : ±arctg wT , которая изменяется от 0 до π/2 при изменении частоты от 0 до ∞ (положительные фазовые сдвиги вносят звенья, которые находятся в числителе а отрицательные – в знаменателе). Идеальное интегрирующее звено на всех частотах вносит фазовый сдвиг –π/2, идеальное дифференцирующее звено +π/2. Для того чтобы определить диапазон изменения ФЧХ достаточно найти суммарный фазовый сдвиг при w=0 и при w ->∞
Правильное соответствие:
-π/2
0
-π
+π/2
Литература: 1. Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 52.
2. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 145.
!True
-π/2
!True
0
!True
-π
!True
+π/2
!Task 32
Установите соответствие между названием типового динамического звена и
максимального значения вносимого им фазового сдвига
1. апериодическое звено первого порядка
2. апериодическое звено второго порядка
3. реальное дифференцирующее звено
4. безынерционное звено
!Solution
Фазовой характеристике инерционных звеньев соответствует одна и та же функция частоты : ±arctg wT , которая изменяется от 0 до π/2 при изменении частоты от 0 до ∞ (положительные фазовые сдвиги вносят звенья, которые находятся в числителе а отрицательные – в знаменателе). Идеальное интегрирующее звено на всех частотах вносит фазовый сдвиг –π/2, идеальное дифференцирующее звено +π/2. Для того чтобы определить диапазон изменения ФЧХ достаточно найти суммарный фазовый сдвиг при w=0 и при w ->∞
Правильное соответствие:
-π/2
-π
+π/2
0
Литература: 1. Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 52.
2. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 145.
!True
-π/2
!True
-π
!True
+π/2
!True
0
!Task 33
Установите соответствие между названием типового динамического звена и
максимального значения вносимого им фазового сдвига
1. апериодическое звено первого порядка
2. реальное дифференцирующее звено
3. безынерционное звено
4. интегрирующее звено с замедление
!Solution
Фазовой характеристике инерционных звеньев соответствует одна и та же функция частоты : ±arctg wT , которая изменяется от 0 до π/2 при изменении частоты от 0 до ∞ (положительные фазовые сдвиги вносят звенья, которые находятся в числителе а отрицательные – в знаменателе). Идеальное интегрирующее звено на всех частотах вносит фазовый сдвиг –π/2, идеальное дифференцирующее звено +π/2. Для того чтобы определить диапазон изменения ФЧХ достаточно найти суммарный фазовый сдвиг при w=0 и при w ->∞
Правильное соответствие:
-π/2
+π/2
0
-π
Литература: 1. Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 52.
2. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 145.
!True
-π/2
!True
+π/2
!True
0
!True
-π
!Task 34
Установите соответствие между названием типового динамического звена и
и диапазоном изменения логарифмической фазовой характеристики (ЛФХ)
1. апериодическое звено первого порядка
2. дифференцирующее звено
3. интегрирующее звено
4. изодром
!Solution
Фазовой характеристике инерционных звеньев соответствует одна и та же функция частоты : ±arctg wT , которая изменяется от 0 до π/2 при изменении частоты от 0 до ∞ (положительные фазовые сдвиги вносят звенья, которые находятся в числителе а отрицательные – в знаменателе). Идеальное интегрирующее звено на всех частотах вносит фазовый сдвиг –π/2, идеальное дифференцирующее звено +π/2. Для того чтобы определить диапазон изменения ФЧХ достаточно найти суммарный фазовый сдвиг при w=0 и при w ->∞
Правильное соответствие:
от 0 до –π/2
+π/2 во всём диапазоне
-π/2 во всём диапазоне
от -π/2 до 0
Литература: 1. Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 52.
2. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 145.
!True
от 0 до –π/2
!True
+π/2 во всём диапазоне
!True
-π/2 во всём диапазоне
!True
от -π/2 до 0
!Task 35
Установите соответствие между названием типового динамического звена и
и диапазоном изменения логарифмической фазовой характеристики (ЛФХ)
1. апериодическое звено первого порядка
2. изодром
3. реальное дифференцирующее звено
4. консервативное звено
!Solution
Фазовой характеристике инерционных звеньев соответствует одна и та же функция частоты : ±arctg wT , которая изменяется от 0 до π/2 при изменении частоты от 0 до ∞ (положительные фазовые сдвиги вносят звенья, которые находятся в числителе а отрицательные – в знаменателе). Идеальное интегрирующее звено на всех частотах вносит фазовый сдвиг –π/2, идеальное дифференцирующее звено +π/2. Для того чтобы определить диапазон изменения ФЧХ достаточно найти суммарный фазовый сдвиг при w=0 и при w ->∞
Правильное соответствие:
от 0 до - π/2
от -π/2 до 0
от +π/2 до 0
от 0 до - π
Литература: 1. Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 52.
2. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 145.
!True
от 0 до - π/2
!True
от -π/2 до 0
!True
от +π/2 до 0
!True
от 0 до - π
!Task 36
Установите соответствие между названием типового динамического звена и
и диапазоном изменения логарифмической фазовой характеристики (ЛФХ)
1. апериодическое звено первого порядка
2. колебательное звено второго порядка
3. безынерционное звено
4. интегрирующее звено
!Solution
Фазовой характеристике инерционных звеньев соответствует одна и та же функция частоты : ±arctg wT , которая изменяется от 0 до π/2 при изменении частоты от 0 до ∞ (положительные фазовые сдвиги вносят звенья, которые находятся в числителе а отрицательные – в знаменателе). Идеальное интегрирующее звено на всех частотах вносит фазовый сдвиг –π/2, идеальное дифференцирующее звено +π/2. Для того чтобы определить диапазон изменения ФЧХ достаточно найти суммарный фазовый сдвиг при w=0 и при w ->∞
Правильное соответствие:
от 0 до - π/2
от 0 до - π
0 во всём диапазоне
-π/2 во всём диапазоне
Литература: 1. Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 52.
2. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 145.
!True
от 0 до - π/2
!True
от 0 до - π
!True
0 во всём диапазоне
!True
-π/2 во всём диапазоне
!Task 37
Установите соответствие между названием типового динамического звена и
и диапазоном изменения логарифмической фазовой характеристики (ЛФХ)
1. реальное дифференцирующее звено
2. колебательное звено второго порядка
3. апериодическое звено первого порядка
4. дифференцирующее звено
!Solution
Фазовой характеристике инерционных звеньев соответствует одна и та же функция частоты : ±arctg wT , которая изменяется от 0 до π/2 при изменении частоты от 0 до ∞ (положительные фазовые сдвиги вносят звенья, которые находятся в числителе а отрицательные – в знаменателе). Идеальное интегрирующее звено на всех частотах вносит фазовый сдвиг –π/2, идеальное дифференцирующее звено +π/2. Для того чтобы определить диапазон изменения ФЧХ достаточно найти суммарный фазовый сдвиг при w=0 и при w ->∞
Правильное соответствие:
от +π/2 до 0
от 0 до - π
от 0 до - π/2
+π/2 во всём диапазоне
Литература: 1. Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 52.
2. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 145.
!True
от +π/2 до 0
!True
от 0 до - π
!True
от 0 до - π/2
!True
+π/2 во всём диапазоне
!Task 38
Установите соответствие между названием типового динамического звена и
и диапазоном изменения логарифмической фазовой характеристики (ЛФХ)
1. изодром
2. реальное дифференцирующее звено
3. дифференцирующее звено
4. интегрирующее звено
!Solution
Фазовой характеристике инерционных звеньев соответствует одна и та же функция частоты : ±arctg wT , которая изменяется от 0 до π/2 при изменении частоты от 0 до ∞ (положительные фазовые сдвиги вносят звенья, которые находятся в числителе а отрицательные – в знаменателе). Идеальное интегрирующее звено на всех частотах вносит фазовый сдвиг –π/2, идеальное дифференцирующее звено +π/2. Для того чтобы определить диапазон изменения ФЧХ достаточно найти суммарный фазовый сдвиг при w=0 и при w ->∞
Правильное соответствие:
от -π/2 до 0
от +π/2 до 0
+π/2 во всём диапазоне
-π/2 во всём диапазоне
Литература: 1. Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 52.
2. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 145.
!True
от -π/2 до 0
!True
от +π/2 до 0
!True
+π/2 во всём диапазоне
!True
-π/2 во всём диапазоне
!Task 39
Установите соответствие между названием типового динамического звена и
и диапазоном изменения логарифмической фазовой характеристики (ЛФХ)
1. апериодическое звено первого порядка
2. колебательное звено второго порядка
3. изодром
4. интегрирующее звено
!Solution
Фазовой характеристике инерционных звеньев соответствует одна и та же функция частоты : ±arctg wT , которая изменяется от 0 до π/2 при изменении частоты от 0 до ∞ (положительные фазовые сдвиги вносят звенья, которые находятся в числителе а отрицательные – в знаменателе). Идеальное интегрирующее звено на всех частотах вносит фазовый сдвиг –π/2, идеальное дифференцирующее звено +π/2. Для того чтобы определить диапазон изменения ФЧХ достаточно найти суммарный фазовый сдвиг при w=0 и при w ->∞
Правильное соответствие:
от 0 до - π/2
от 0 до - π
от -π/2 до 0
-π/2 во всём диапазоне
Литература: 1. Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 52.
2. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 145.
!True
от 0 до - π/2
!True
от 0 до - π
!True
от -π/2 до 0
!True
-π/2 во всём диапазоне
!Task 40
Установите соответствие между названием типового динамического звена и
и диапазоном изменения логарифмической фазовой характеристики (ЛФХ)
1. консервативное звено
2. апериодическое звено первого порядка
3. изодром
4. реальное дифференцирующее звено
!Solution
Фазовой характеристике инерционных звеньев соответствует одна и та же функция частоты : ±arctg wT , которая изменяется от 0 до π/2 при изменении частоты от 0 до ∞ (положительные фазовые сдвиги вносят звенья, которые находятся в числителе а отрицательные – в знаменателе). Идеальное интегрирующее звено на всех частотах вносит фазовый сдвиг –π/2, идеальное дифференцирующее звено +π/2. Для того чтобы определить диапазон изменения ФЧХ достаточно найти суммарный фазовый сдвиг при w=0 и при w ->∞
Правильное соответствие:
от 0 до - π
от 0 до - π/2
от -π/2 до 0
от +π/2 до 0
Литература: 1. Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 52.
2. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 145.
!True
от 0 до - π
!True
от 0 до - π/2
!True
от -π/2 до 0
!True
от +π/2 до 0
!Task 41
Установите соответствие между названиями динамических звеньев и АФЧХ
1. апериодическое 1 порядка
2. апериодическое 2 порядка
3. колебательное
4. дифференцирующее с замедлением
!Solution
Амплитудно-фазовая частотная характеристика строится на комплексной плоскости. Она представляет собой геометрическое место концов векторов (годограф), соответствующих частотной передаточной функции. W(jw)=U(w)+jV(w) при изменении частоты от нуля до бесконечности.
Гораздо проще её строить, используя полярные координаты, т.е. вычисляя непосредственно модуль и фазу. Зная их можно легко построить соответствующую точку на комплексной плоскости. В случае необходимости, при известных модуле и фазе легко вычислить вещественную и мнимую части умножением модуля на направляющий косинус между вектором и соответствующей осью.
Правильное соответствие: 1.

2.

3.

4.

Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 56.
!True

!True

!True

!True

!Task 42
Установите соответствие между названиями динамических звеньев и АФЧХ
1. идеальное дифференцирующее
2. идеальное интегрирующее
3. изодромное
4. консервативное
!Solution
Амплитудно-фазовая частотная характеристика строится на комплексной плоскости. Она представляет собой геометрическое место концов векторов (годограф), соответствующих частотной передаточной функции. W(jw)=U(w)+jV(w) при изменении частоты от нуля до бесконечности.
Гораздо проще её строить, используя полярные координаты, т.е. вычисляя непосредственно модуль и фазу. Зная их можно легко построить соответствующую точку на комплексной плоскости. В случае необходимости, при известных модуле и фазе легко вычислить вещественную и мнимую части умножением модуля на направляющий косинус между вектором и соответствующей осью.
Правильное соответствие: 1.

2.

3.

4.

Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 56.
!True

!True

!True
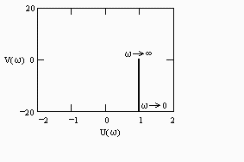
!True

!Task 43
Установите соответствие между названиями динамических звеньев и АФЧХ
1. апериодическое 2 порядка
2. колебательное
3. идеальное дифференцирующее
4. интегрирующее с замедлением
!Solution
Амплитудно-фазовая частотная характеристика строится на комплексной плоскости. Она представляет собой геометрическое место концов векторов (годограф), соответствующих частотной передаточной функции. W(jw)=U(w)+jV(w) при изменении частоты от нуля до бесконечности.
Гораздо проще её строить, используя полярные координаты, т.е. вычисляя непосредственно модуль и фазу. Зная их можно легко построить соответствующую точку на комплексной плоскости. В случае необходимости, при известных модуле и фазе легко вычислить вещественную и мнимую части умножением модуля на направляющий косинус между вектором и соответствующей осью.
Правильное соответствие: 1.

2.
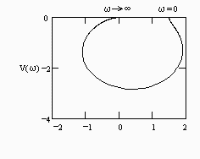
3.

4.

Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 56.
!True

!True

!True

!True

!Task 44
Установите соответствие между названиями динамических звеньев и АФЧХ
1. апериодическое 1 порядка
2. дифференцирующее с замедлением
3. консервативное
4. изодромное
!Solution
Амплитудно-фазовая частотная характеристика строится на комплексной плоскости. Она представляет собой геометрическое место концов векторов (годограф), соответствующих частотной передаточной функции. W(jw)=U(w)+jV(w) при изменении частоты от нуля до бесконечности.
Гораздо проще её строить, используя полярные координаты, т.е. вычисляя непосредственно модуль и фазу. Зная их можно легко построить соответствующую точку на комплексной плоскости. В случае необходимости, при известных модуле и фазе легко вычислить вещественную и мнимую части умножением модуля на направляющий косинус между вектором и соответствующей осью.
Правильное соответствие: 1.

2.
3.

4.

Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 56.
!True

!True

!True

!True

!Task 45
Установите соответствие между названиями динамических звеньев и АФЧХ
1. интегрирующее с замедлением
2. изодромное
3. безынерционное
4. идеальное интегрирующее
!Solution
Амплитудно-фазовая частотная характеристика строится на комплексной плоскости. Она представляет собой геометрическое место концов векторов (годограф), соответствующих частотной передаточной функции. W(jw)=U(w)+jV(w) при изменении частоты от нуля до бесконечности.
Гораздо проще её строить, используя полярные координаты, т.е. вычисляя непосредственно модуль и фазу. Зная их можно легко построить соответствующую точку на комплексной плоскости. В случае необходимости, при известных модуле и фазе легко вычислить вещественную и мнимую части умножением модуля на направляющий косинус между вектором и соответствующей осью.
Правильное соответствие: 1.
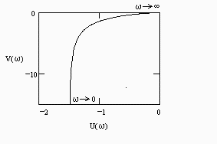
2.
3.
4.

Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 56.
!True

!True

!True

!True

!END
*********************************************
*ОТУ 1.2.02.t2.rtf
*********************************************
!Taskfile ОТУ 1.2.02.# Временные и частотные характеристики типовых динамических звеньев
!DE=ОТУ 1.2.#Структурные представления систем управления
!Type=2
!Time=2
Экспертные и технологические параметры заданий:
1. Дисциплина: Основы теории управления
2. Объем часов: группа I (от 80 до 170 часов)
3. Дидактическая единица ГОС: Структурные представления систем управления
4. Тема задания: Временные и частотные характеристики типовых динамических звеньев
5. Уровень сложности: 1 (знать и использовать в типовой учебной ситуации)
6. Ориентировочное время выполнения: 2 минуты
7. Перечень контролируемых учебных элементов
Студент должен знать: временные характеристики – переходные, весовые функции и частотные характеристики - амплитудно-фазо-частотные и логарифмические амплитудно-фазо-частотные типовых звеньев
8. Форма заданий: выбор одного ответа из четырех предложенных
!Task 1
Реакцией
звена с передаточной функцией 
 на единичное ступенчатое входное
воздействие является …
на единичное ступенчатое входное
воздействие является …
!Solution
Звено
с передаточной функцией
является апериодическим звеном первого
порядка, где
 –
это коэффициент передачи звена,
–
это коэффициент передачи звена,
 –
это постоянная времени. Переходная
функция представляет собой экспоненту.
–
это постоянная времени. Переходная
функция представляет собой экспоненту.
Правильный ответ:
экспонента.
Литература:
Бесекерский В.А., Попов Е.П. Теория систем автоматического управления. – Изд. 4-е, перераб. и доп. - СПб: Профессия, 2007 г. – с. 60-62.
!True
экспонента
!False
затухающие гармонические колебания
!False
гармонические колебания постоянной амплитуды
!False
линейно нарастающий сигнал
!Task 2
Реакцией
звена с передаточной функцией 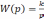
 на единичное ступенчатое входное
воздействие является …
на единичное ступенчатое входное
воздействие является …
!Solution
Звено с передаточной функцией является идеальным интегрирующим звеном, где – это коэффициент передачи звена. Переходная функция представляет собой линейно нарастающий сигнал.
Правильный ответ:
линейно нарастающий сигнал.
Литература:
Бесекерский В.А., Попов Е.П. Теория систем автоматического управления. – Изд. 4-е, перераб. и доп. - СПб: Профессия, 2007 г. – с. 73-74.
!True
линейно нарастающий сигнал
!False
затухающие гармонические колебания
!False
экспонента
!False
гармонические колебания постоянной амплитуды
!Task 3
Реакцией
звена с передаточной функцией 
 на единичное ступенчатое входное
воздействие является …
на единичное ступенчатое входное
воздействие является …
!Solution
Звено
с передаточной функцией
является колебательным звеном, где
–
это коэффициент передачи звена,
–
это постоянная времени,
 -
это параметр затухания. Переходная
функция представляет собой затухающие
гармонические колебания.
-
это параметр затухания. Переходная
функция представляет собой затухающие
гармонические колебания.
Правильный ответ:
затухающие гармонические колебания.
Литература:
Бесекерский В.А., Попов Е.П. Теория систем автоматического управления. – Изд. 4-е, перераб. и доп. - СПб: Профессия, 2007 г. – с. 69-70.
!True
затухающие гармонические колебания
!False
линейно нарастающий сигнал
!False
гармонические колебания постоянной амплитуды
!False
экспонента
!Task 4
Реакцией
звена с передаточной функцией 
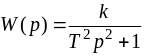 на единичное ступенчатое входное
воздействие является …
на единичное ступенчатое входное
воздействие является …
!Solution
Звено с передаточной функцией является консервативным звеном, частным случаем колебательного звена, где – это коэффициент передачи звена, – это постоянная времени, а параметр затухания . Переходная функция представляет собой гармонические колебания постоянной амплитуды.
Правильный ответ:
гармонические колебания постоянной амплитуды .
Литература:
Бесекерский В.А., Попов Е.П. Теория систем автоматического управления. – Изд. 4-е, перераб. и доп. - СПб: Профессия, 2007 г. – с. 71-73.
!True
гармонические колебания постоянной амплитуды
!False
линейно нарастающий сигнал
!False
затухающие гармонические колебания
!False
экспонента
!Task 5
Реакцией звена с передаточной функцией
W(p)=k
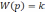 на
единичное ступенчатое входное воздействие
является …
на
единичное ступенчатое входное воздействие
является …
!Solution
Звено
с передаточной функцией
W(p)=k
является
безынерционным звеном, где коэффициент
передачи звена величина постоянная.
Переходная функция представляет собой
ступенчатую функцию, т.е. при x1(t)=1(t),
x2(t)=k
1(t),
где x1(t)-
входная величина, x2(t)
–
выходная.
Правильный ответ:
ступенчатая функция.
Литература:
Бесекерский В.А., Попов Е.П. Теория систем автоматического управления. – Изд. 4-е, перераб. и доп. - СПб: Профессия, 2007 г. – с. 60.
!True
ступенчатая функция
!False
линейно нарастающий сигнал
!False
гармонические колебания
!False
экспонента
!Task 6
Переходная функция звена с передаточной функцией
W(p)=kp
 имеет
вид …
имеет
вид …
!Solution
Звено
с передаточной функцией
является идеальным дифференцирующим
звеном, где k
коэффициент
передачи звена величина постоянная.
Переходная функция имеет вид  h(t)=k
δ(t),
т.е. представляет собой дельта-функцию.
h(t)=k
δ(t),
т.е. представляет собой дельта-функцию.
Правильный ответ:
дельта-функция .
Литература:
Бесекерский В.А., Попов Е.П. Теория систем автоматического управления. – Изд. 4-е, перераб. и доп. - СПб: Профессия, 2007 г. – с. 78-79.
!True
дельта-функция
!False
ступенчатая функция
 !False
!False
экспонента
!False
линейно нарастающий сигнал
!Task 7
Переходная функция звена с передаточной функцией
W(p)=kp/(Tp+1)
 имеет
вид …
имеет
вид …
!Solution
Звено с передаточной функцией
W(p)=kp/(Tp+1)
является
дифференцирующим звеном c
замедлением, где
–
это коэффициент передачи звена, T–
постоянная времени. Переходная функция
имеет вид 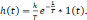
Правильный ответ:
 убывающей
экспоненты
убывающей
экспоненты
Литература:
Бесекерский В.А., Попов Е.П. Теория систем автоматического управления. – Изд. 4-е, перераб. и доп. - СПб: Профессия, 2007 г. – с. 79-81.
!True
убывающей экспоненты
!False
ступенчатой функции
!False
линейно нарастающей функции
!False
нарастающей экспоненты
!Task 8
Переходная функция звена с передаточной функцией

имеет вид …
!Solution
Звено
с передаточной функцией
является безынерционным звеном, где
 –
это коэффициент передачи звена, постоянная
величина. Переходная функция представляет
собой ступенчатую функцию, т.е. при
–
это коэффициент передачи звена, постоянная
величина. Переходная функция представляет
собой ступенчатую функцию, т.е. при
 .
.
Правильный
ответ:
 .
.
Литература:
Бесекерский В.А., Попов Е.П.Теория систем автоматического управления. – Изд. 4-е, перераб. и доп. - СПб: Профессия, 2003 г. – с. 60.
!True

!False

!False

!False
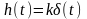
!Task 9
Переходная функция звена с передаточной функцией


имеет вид …
!Solution
Звено
с передаточной функцией
является изодромным звеном, где
–
это коэффициент передачи звена, 
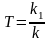 .
Переходная функция изодромного звена
имеет вид
.
Переходная функция изодромного звена
имеет вид 
 .
.
Правильный ответ: .
Литература:
Бесекерский В.А., Попов Е.П.Теория систем автоматического управления. – Изд. 4-е, перераб. и доп. - СПб: Профессия, 2003 г. – с. 77-78.
!True

!False

!False
!False

!Task 10
Переходная функция звена с передаточной функцией

имеет вид …
!Solution
Звено
с передаточной функцией
является консервативным звеном, где
–
это коэффициент передачи звена,
 –
это постоянная времени. Переходная
функция консервативного звена имеет
вид
–
это постоянная времени. Переходная
функция консервативного звена имеет
вид 
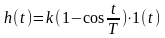 .
.
Правильный ответ:
.
Литература:
Бесекерский В.А., Попов Е.П.Теория систем автоматического управления. – Изд. 4-е, перераб. и доп. - СПб: Профессия, 2003 г. – с. 71-73.
!True

!False


!False
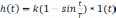

!False
!Task 11
Переходная функция звена с передаточной функцией


имеет
вид …

!Solution
Звено
с передаточной функцией
является интегрирующим звеном с
замедлением, где
–
это коэффициент передачи звена,
–
это постоянная времени. Переходная
функция интегрирующего звена с замедлением
имеет вид 
 .
.
Правильный ответ:
 .
.
Литература:
Бесекерский В.А., Попов Е.П.Теория систем автоматического управления. – Изд. 4-е, перераб. и доп. - СПб: Профессия, 2003 г. – с. 75-77.
!True
!False
!False


!False
!Task 12
Переходная
функция звена с передаточной функцией
 имеет вид …
имеет вид …
!Solution
Звено
с передаточной функцией
является апериодическим звеном 1-ого
порядка, где
–
это коэффициент передачи звена,
–
это постоянная времени. Переходная
функция апериодического звена 1-ого
порядка представляет собой экспоненту
и имеет вид
 .
.
Правильный ответ:
.
Литература:
Бесекерский В.А., Попов Е.П.Теория систем автоматического управления. – Изд. 4-е, перераб. и доп. - СПб: Профессия, 2003 г. – с. 60-62.
!True
!False
!False
!False
!Task 13
Переходная
функция звена с передаточной функцией
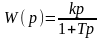 имеет вид …
имеет вид …
!Solution
Звено
с передаточной функцией
 является дифференцирующим звеном c
замедлением, где
–
это коэффициент передачи звена,
–
это постоянная времени. Переходная
функция имеет вид
является дифференцирующим звеном c
замедлением, где
–
это коэффициент передачи звена,
–
это постоянная времени. Переходная
функция имеет вид
Правильный ответ: .
Литература:
Бесекерский В.А., Попов Е.П.Теория систем автоматического управления. – Изд. 4-е, перераб. и доп. - СПб: Профессия, 2003 г. – с. 79-81.
!True
!False
!False
!False

!Task 14
Звено, функция веса которого представлена на следующем рисунке, называется …

!Solution
Из
теории временных характеристик типовых
динамических звеньев известно, что
функция веса апериодического звена
первого порядка имеет вид: 

Правильный ответ: Апериодическое звено первого порядка.
Литература:
Бесекерский В.А., Попов Е.П.Теория систем автоматического управления. – Изд. 4-е, перераб. и доп. - СПб: Профессия, 2003 г. – с. 60-62.
!True
апериодическое звено первого порядка
!False
апериодическое звено первого порядка
!False
дифференцирующее звено с замедлением
!False
интегрирующее звено с замедлением
!Task 15
Звено, переходная функция которого представлена на следующем рисунке, называется …

!Solution
Из теории временных характеристик типовых динамических звеньев известно, что переходная функция дифференцирующего звена с замедлением
имеет
вид:
 .
.
Правильный ответ:
дифференцирующее звено с замедлением
Литература:
Бесекерский В.А., Попов Е.П. Теория систем автоматического управления. – Изд. 4-е, перераб. и доп. - СПб: Профессия, 2007 г. – с. 79-81.
!True
дифференцирующее звено с замедлением
!False
апериодическое звено первого порядка
!False
апериодическое звено первого порядка
!False
интегрирующее звено с замедлением
!Task 16
НЕ является позиционным …
!Solution
К позиционным звеньям относятся: безынерционное звено, апериодическое звено первого порядка, апериодическое звено второго порядка, колебательное звено, консервативное звено.
Правильный ответ:
изодромное звено.
Литература:
Бесекерский В.А., Попов Е.П. Теория систем автоматического управления. – Изд. 4-е, перераб. и доп. - СПб: Профессия, 2007 г. – с. 60-73.
!True
изодромное звено
!False
апериодическое звено первого порядка
!False
колебательное звено
!False
безынерционное звено
!Task 17
НЕ является позиционным …
!Solution
К позиционным звеньям относятся: безынерционное звено, апериодическое звено первого порядка, апериодическое звено второго порядка, колебательное звено, консервативное звено.
Правильный ответ:
интегрирующее звено.
Литература:
Бесекерский В.А., Попов Е.П. Теория систем автоматического управления. – Изд. 4-е, перераб. и доп. - СПб: Профессия, 2007 г. – с. 60-73.
!True
интегрирующее звено
!False
апериодическое звено первого порядка
!False
колебательное звено
!False
безынерционное звено
!Task 18
НЕ является позиционным …
!Solution
К позиционным звеньям относятся: безынерционное звено, апериодическое звено первого порядка, апериодическое звено второго порядка, колебательное звено, консервативное звено.
Правильный ответ:
дифференцирующее звено.
Литература:
Бесекерский В.А., Попов Е.П. Теория систем автоматического управления. – Изд. 4-е, перераб. и доп. - СПб: Профессия, 2007 г. – с. 60-73.
!True
дифференцирующее звено
!False
апериодическое звено первого порядка
!False
колебательное звено
!False
безынерционное звено
!Task 19
НЕ является позиционным …
!Solution
К позиционным звеньям относятся: безынерционное звено, апериодическое звено первого порядка, апериодическое звено второго порядка, колебательное звено, консервативное звено.
Правильный ответ:
интегрирующее с замедлением звено.
Литература:
Бесекерский В.А., Попов Е.П. Теория систем автоматического управления. – Изд. 4-е, перераб. и доп. - СПб: Профессия, 2007 г. – с. 60-73.
!True
интегрирующее с замедлением звено
!False
апериодическое звено первого порядка
!False
колебательное звено
!False
безынерционное звено
!Task 20
Позиционным звеном является …
!Solution
К позиционным звеньям относятся: безынерционное звено, апериодическое звено первого порядка, апериодическое звено второго порядка, колебательное звено, консервативное звено.
Правильный ответ:
консервативное звено
Литература:
Бесекерский В.А., Попов Е.П. Теория систем автоматического управления. – Изд. 4-е, перераб. и доп. - СПб: Профессия, 2007 г. – с. 60-73.
!True
консервативное
!False
интегрирующее
!False
изодромное
!False
идеальное дифференцирующее
!Task 21
Позиционным звеном является …
!Solution
К позиционным звеньям относятся: безынерционное звено, апериодическое звено первого порядка, апериодическое звено второго порядка, колебательное звено, консервативное звено.
Правильный ответ:
колебательное.
Литература:
Бесекерский В.А., Попов Е.П. Теория систем автоматического управления. – Изд. 4-е, перераб. и доп. - СПб: Профессия, 2007 г. – с. 60-73.
!True
колебательное
!False
интегрирующее
!False
изодромное
!False
идеальное дифференцирующее
!Task 22
Позиционным звеном является …
!Solution
К позиционным звеньям относятся: безынерционное звено, апериодическое звено первого порядка, апериодическое звено второго порядка, колебательное звено, консервативное звено.
Правильный ответ:
безынерционное звено
Литература:
Бесекерский В.А., Попов Е.П. Теория систем автоматического управления. – Изд. 4-е, перераб. и доп. - СПб: Профессия, 2007 г. – с. 60-73.
!True
безынерционное
!False
интегрирующее
!False
изодромное
!False
идеальное дифференцирующее
!Task 23
Позиционным звеном является …
!Solution
К позиционным звеньям относятся: безынерционное звено, апериодическое звено первого порядка, апериодическое звено второго порядка, колебательное звено, консервативное звено.
Правильный ответ:
апериодическое первого порядка
Литература:
Бесекерский В.А., Попов Е.П. Теория систем автоматического управления. – Изд. 4-е, перераб. и доп. - СПб: Профессия, 2007 г. – с. 60-73.
!True
апериодическое первого порядка
!False
интегрирующее
!False
изодромное
!False
идеальное дифференцирующее
!Task 24
Позиционным звеном является …
!Solution
К позиционным звеньям относятся: безынерционное звено, апериодическое звено первого порядка, апериодическое звено второго порядка, колебательное звено, консервативное звено.
Правильный ответ:
апериодическое звено второго порядка
Литература:
Бесекерский В.А., Попов Е.П. Теория систем автоматического управления. – Изд. 4-е, перераб. и доп. - СПб: Профессия, 2007 г. – с. 60-73.
!True
апериодическое второго порядка
!False
интегрирующее
!False
изодромное
!False
идеальное дифференцирующее
!Task 25
Интегрирующим звеном является …
!Solution
К интегрирующим звеньям относятся: идеальное интегрирующее, интегрирующее с замедлением, изодромное звено.
Правильный ответ:
изодромное.
Литература:
Бесекерский В.А., Попов Е.П. Теория систем автоматического управления. – Изд. 4-е, перераб. и доп. - СПб: Профессия, 2007 г. – с. 73-78.
!True
изодромное
!False
колебательное
!False
консервативное
!False
апериодическое
!Task 26
Основное свойство дельта-функции заключается в том, что она …
!Solution
Единичная
импульсная функция или дельта-функция
представляет собой производную от
единичной ступенчатой функции .Основное
свойство дельта-функции заключается в
том, что  ,
т.е. она имеет единичную площадь.
,
т.е. она имеет единичную площадь.
Правильный ответ:
имеет единичную площадь.
Литература:
Бесекерский В.А., Попов Е.П. Теория систем автоматического управления. – Изд. 4-е, перераб. и доп. - СПб: Профессия, 2007 г. – с. 52.
!True
имеет единичную площадь
!False
представляет собой производную от единичной ступенчатой функции
!False
непрерывна
!False
устанавливает связь между переходной функцией и функцией веса
!Task 27
Динамические свойства звена могут быть определены по функции …
!Solution
Из теории временных характеристик типовых динамических звеньев известно, что динамические свойства звена могут быть определены по его переходной функции и функции веса.
Правильный ответ:
переходная функция и функция веса.
Литература:
Бесекерский В.А., Попов Е.П. Теория систем автоматического управления. – Изд. 4-е, перераб. и доп. - СПб: Профессия, 2007 г. – с. 60-62.
!True
переходная функция и функция веса
!True
веса
!False
массы
!False
трансферной
!Task 28
Логарифмическая амплитудная частотная характеристика (ЛАЧХ) колебательного звена имеет наклон высокочастотной асимптоты ______ дБ/дек.
!Solution
При возрастании w строим асимптотическую ЛАХ, как ломанную линию, прямолинейные отрезки которой изменяют наклон при сопрягающих частотах wi на ±20 дБ/дек, если wi – принадлежит звену первого порядка, ±40 дБ/дек – звену второго порядка и т.д. Здесь + соответствует форсирующему звену (числитель ПФ ), а – - инерционному звену (знаменатель ПФ).
В случае колебательного звена низкочастотная часть будет иметь наклон 0 дБ/дек до сопрягающей частоты после неё наклон составит – 40 дБ/дек .
Правильный ответ: -40 дБ/дек.
Литература: 1. Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 88.
!True
-40
!False
0
!False
-20
!False
40
!Task 29
Логарифмическая амплитудно-частотная характеристика (ЛАЧХ) последовательно соединённых звеньев определяется как …
!Solution
При последовательном соединении двух звеньев ЛАФХ определяется как сумма характеристик составляющих звеньев:
L(w)=L1(w)+L2(w) ;
Правильный ответ: как сумма ЛАЧХ отдельных звеньев.
Литература: 1. Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 66.
!True
сумма ЛАЧХ отдельных звеньев
!False
разность ЛАЧХ отдельных звеньев
!False
произведение ЛАЧХ отдельных звеньев
!False
отношение ЛАЧХ отдельных звеньев
!Task 30
Низкочастотная асимптота имеет положительный наклон в 20 дб/дек у звена …
!Solution
При возрастании w строим асимптотическую ЛАХ, как ломанную линию, прямолинейные отрезки которой изменяют наклон при сопрягающих частотах wi на ±20 дБ/дек, если wi – принадлежит звену первого порядка, ±40 дБ/дек – звену второго порядка и т.д. Здесь + соответствует форсирующему звену (числитель ПФ ), а – - инерционному звену (знаменатель ПФ).
Правильный ответ: дифференциирующего звена с замедлением.
Литература: 1. Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 88.
!True
дифференцирующего с замедлением
!False
апериодического первого порядка
!False
колебательного
!False
интегрирующего
!Task 31
Фазовый сдвиг, вносимый дифференцирующим звеном, равен …
!Solution
Частотные функции данного звена определяются формулами:
 ,
A(w)=kw,
,
A(w)=kw,
а
фазовая характеристика во всём диапазоне
частот будет вносить фазовый сдвиг
равный + .
.
Правильный ответ: +π/2
Литература: Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 55.
!True
+π/2
!False
-π/2
!False
+π
!False
-3π/2
!Task 33
Фазовый сдвиг, вносимый интегрирующим звеном, равен …
!Solution
Частотные функции данного звена определяются формулами:
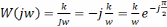 ,
A(w)=
,
A(w)= ,
,
а фазовая характеристика во всём диапазоне частот будет вносить фазовый сдвиг равный - .
Правильный ответ: -π/2
Литература: Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 55.
!True
-π/2
!False
+π/2
!False
+π
!False
-3π/2
!Task 34
Максимальное расхождение между действительной ЛАЧХ и асимптотической ЛАЧХ апериодического звена 1-го порядка составляет _____ дБ.
!Solution
Логарифмическая амплитудно частотная характеристика апериодического звена
1-ого порядка определяется выражением:

Для практических расчетов, как правило , можно пользоваться приближенной асимптотической ЛАЧХ. Эта характеристика для данного звена состоит из низкочастотной и высокочастотной асимптот:
 .
.
Общей точке (точке сопряжения) этих асимптот соответствует частота
 ,
поэтому она называется сопрягающей
частотой. В этой точке и будет наибольшее
отличие асимтотической ЛАЧХ от реальной.
Эта погрешность составляет 3 дБ, что
считается допустимым.
,
поэтому она называется сопрягающей
частотой. В этой точке и будет наибольшее
отличие асимтотической ЛАЧХ от реальной.
Эта погрешность составляет 3 дБ, что
считается допустимым.
Правильный ответ: 3 дБ.
Литература: Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 60.
!True
3
!False
2
!False
1
!False
0
!Task 35
Положительный наклон асимптотической логарифмической амплитудной частотной характеристики имеют звенья …
!Solution
Асимптотические ЛАЧХ дифференцирующих звеньев имееют положительный наклон либо во всём частотном диапазоне как идеальное дифференцирующее звено, либо в низко частотной части диапазона, что имеет место у дифференцирующих звеньев с замедлением.
Правильный ответ:
дифференцирующие звенья.
Литература: 1.Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 55.
!True
дифференцирующие
!False
интегрирующие
!False
позиционные
!False
минимально-фазовые
!Task 36
Логарифмическая амплитудная частотная характеристика апериодического звена первого порядка имеет вид …
!Solution
При возрастании w строим асимптотическую ЛАХ, как ломанную линию, прямолинейные отрезки которой изменяют наклон при сопрягающих частотах wi на ±20 дБ/дек, если wi – принадлежит звену первого порядка, ±40 дБ/дек – звену второго порядка и т.д. Здесь + соответствует форсирующему звену (числитель ПФ), а – - инерционному звену (знаменатель ПФ). В данном случае можно не определяя значений сопрягающих частот сказать, что максимальный наклон, который дает знаменатель ПФ апериодического звена первого порядка – -20 дБ/дек., низкочастотная часть до сопрягающей частоты имеет наклон 0 дБ/дек.
Правильный
ответ:

Литература: 1. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 44-47.
!True

!False
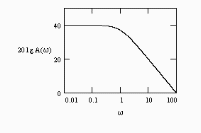
!False

!False

!Task 37
Логарифмическая амплитудная частотная характеристика апериодического звена второго порядка имеет вид …
!Solution
При возрастании w строим асимптотическую ЛАХ, как ломанную линию, прямолинейные отрезки которой изменяют наклон при сопрягающих частотах wi на ±20 дБ/дек, если wi – принадлежит звену первого порядка, ±40 дБ/дек – звену второго порядка и т.д. Здесь + соответствует форсирующему звену (числитель ПФ), а – - инерционному звену (знаменатель ПФ). В данном случае можно не определяя значений сопрягающих частот сказать, что максимальный наклон, который дает знаменатель ПФ апериодического звена второго порядка – -40 дБ/дек., низкочастотная часть до сопрягающей частоты имеет наклон 0 дБ/дек.
Правильный ответ:
Литература: 1. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 44-47.
!True

!False
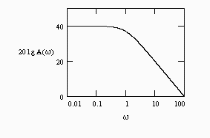
!False

!False

!Task 38
Наклон асимптотической логарифмической амплитудной частотной характеристики звена с передаточной функцией

равен ______ дБ/дек.
!Solution
При возрастании w строим асимптотическую ЛАХ, как ломанную линию, прямолинейные отрезки которой изменяют наклон при сопрягающих частотах wi на ±20 дБ/дек, если wi – принадлежит звену первого порядка, ±40 дБ/дек – звену второго порядка и т.д. Здесь + соответствует форсирующему звену (числитель ПФ), а – - инерционному звену (знаменатель ПФ). В данном случае можно сказать, что во всём частотном диапазоне наклон составит -20 дБ/дек (интегрирующее звено).
!True
-20
!False
+20
!False
-40
!False
+40
!Task 39
На рисунке представлены логарифмические амплитудо-частотные и фазо-частотные характеристики звена …

!Solution
При возрастании w строим асимптотическую ЛАХ, как ломанную линию, прямолинейные отрезки которой изменяют наклон при сопрягающих частотах wi на ±20 дБ/дек, если wi – принадлежит звену первого порядка, ±40 дБ/дек – звену второго порядка и т.д. Здесь + соответствует форсирующему звену (числитель ПФ ), а – - инерционному звену (знаменатель ПФ). Таким образом, можно восстановить передаточную функцию: низкочастотная часть представляет идеальное дифференцирующее звено, а высокочастотная часть характеристики представлена апериодическим звеном первого порядка. Т.е. имеет вид:
 ,
что описывает изодромное звено.
,
что описывает изодромное звено.
Правильный ответ: изодромного
Литература: 1. Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 88.
!True
изодромного
!False
идеального дифференцирующего
!False
дифференцирующего с замедлением
!False
интегрирующего с замедлением
!Task 40
На рисунке представлены логарифмические амплитудо-частотные и фазо-частотные характеристики звена …

!Solution
При возрастании w строим асимптотическую ЛАХ, как ломанную линию, прямолинейные отрезки которой изменяют наклон при сопрягающих частотах wi на ±20 дБ/дек, если wi – принадлежит звену первого порядка, ±40 дБ/дек – звену второго порядка и т.д. Здесь + соответствует форсирующему звену (числитель ПФ ), а – - инерционному звену (знаменатель ПФ). Таким образом, можно восстановить передаточную функцию: низкочастотная часть представляет идеальное дифференцирующее звено, а высокочастотная часть характеристики представлена апериодическим звеном первого порядка. Т.е. имеет вид:
 ,
что описывает колебательное звено.
,
что описывает колебательное звено.
Правильный ответ: колебательного звена
Литература: 1. Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 88.
!True
колебательного
!False
консервативного
!False
изодромного
!False
интегрирующего
!END
*********************************************
*ОТУ 1.2.03.t2.rtf
*********************************************
!Taskfile ОТУ 1.2.03.#Анализ временных и частотных характеристик типовых динамических звеньев
!DE=ОТУ 1.2.#Структурные представления систем управления
!Type=2
!Time=2
Экспертные и технологические параметры заданий:
1. Дисциплина: Основы теории управления
2. Объем часов: группа I (от 80 до 170 часов)
3. Дидактическая единица ГОС: Структурные представления систем управления
4. Тема задания: Анализ временных и частотных характеристик типовых динамических звеньев
5. Уровень сложности: 2 (знать и уметь использовать в типовой учебной ситуации)
6. Ориентировочное время выполнения: 2 минуты
7. Перечень контролируемых учебных элементов
Студент должен знать: временные и частотные характеристики типовых звеньев
уметь: определять параметры звеньев по временным и частотным характеристикам
8. Форма заданий: выбор одного ответа из четырех предложенных
!Task 1
Аналитическое выражение для мнимой части частотной передаточной функции апериодического звена 1-го порядка имеет вид …
!Solution
Частотная передаточная функция W(jw) представляет собой комплексное число, модуль которого равен отношению амплитуды выходной величины к амплитуде входной, а аргумент – сдвигу фаз выходной величины по отношению к входной. Частотная передаточная функция может быть представлена в следующем виде:
![]()
Для нахождения вещественной и мнимой частей частотной передаточной функции необходимо освободиться от мнимости в знаменателе путем умножения числителя и знаменателя на комплексную величину, сопряженную знаменателю, и затем произвести разделение на вещественную и мнимую части.
Правильный
ответ:
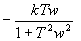
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб., Профессия. 2007, 752 с., стр. 55-56.
!True
!False
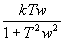
!False

!False
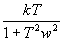
!Task 2
Постоянная времени звена, переходная функция которого представлена на рисунке равна …
равна:
!Solution
Из теории временных характеристик типовых динамических звеньев известно, что переходная функция дифференцирующего звена с замедлением
имеет
вид:

![]() .
.
 (расстояние от нуля до точки пересечения
касательной к переходной функции с осью
абсцисс).
(расстояние от нуля до точки пересечения
касательной к переходной функции с осью
абсцисс). ![]()
 (расстояние от нуля до начальной точки
функции (при
(расстояние от нуля до начальной точки
функции (при ![]()
 )
на оси ординат). Следовательно,
)
на оси ординат). Следовательно, ![]()
 .
.
Правильный ответ:
.
Литература:
Бесекерский В.А., Попов Е.П. Теория систем автоматического управления. – Изд. 4-е, перераб. и доп. - СПб: Профессия, 2007 г. – с. 79-81.
!True
![]()
!False

!False

!False

!Task 3
Постоянная времени звена, переходная функция которого представлена на рисунке равна …
равна:
!Solution
Из теории временных характеристик типовых динамических звеньев известно, что переходная функция дифференцирующего звена с замедлением
имеет
вид:
.
 (расстояние от нуля до точки пересечения
касательной к переходной функции с осью
абсцисс).
(расстояние от нуля до точки пересечения
касательной к переходной функции с осью
абсцисс).
 (расстояние от нуля до начальной точки
функции (при
)
на оси ординат). Следовательно,
(расстояние от нуля до начальной точки
функции (при
)
на оси ординат). Следовательно,
 .
.
Правильный ответ:
.
Литература:
Бесекерский В.А., Попов Е.П. Теория систем автоматического управления. – Изд. 4-е, перераб. и доп. - СПб: Профессия, 2007 г. – с. 79-81.
!True
![]()
!False

!False

!False

!Task 4
Коэффициент передачи звена, переходная функция которого представлена на следующем рисунке равен …
равен:
!Solution
Из теории временных характеристик типовых динамических звеньев известно, что переходная функция дифференцирующего звена с замедлением
имеет
вид:
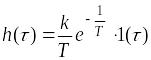 .
(расстояние от нуля до точки пересечения
касательной к переходной функции с осью
абсцисс).
.
(расстояние от нуля до точки пересечения
касательной к переходной функции с осью
абсцисс).
![]() (расстояние от нуля до начальной точки
функции (при
(расстояние от нуля до начальной точки
функции (при
![]() )
на оси ординат). Следовательно,
.
)
на оси ординат). Следовательно,
.
Правильный
ответ:![]()
![]() .
.
Литература:
Бесекерский В.А., Попов Е.П. Теория систем автоматического управления. – Изд. 4-е, перераб. и доп. - СПб: Профессия, 2007 г. – с. 79-81.
!True
!False

!False
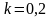
!False

!Task 5
Коэффициент передачи звена, переходная функция которого представлена на следующем рисунке равен …
равен:
!Solution
Из теории временных характеристик типовых динамических звеньев известно, что переходная функция дифференцирующего звена с замедлением
имеет
вид:
.
(расстояние от нуля до точки пересечения
касательной к переходной функции с осью
абсцисс).
![]() (расстояние от нуля до начальной точки
функции (при
)
на оси ординат). Следовательно,
.
(расстояние от нуля до начальной точки
функции (при
)
на оси ординат). Следовательно,
.
Правильный ответ:
![]() .
.
Литература:
Бесекерский В.А., Попов Е.П. Теория систем автоматического управления. – Изд. 4-е, перераб. и доп. - СПб: Профессия, 2007 г. – с. 79-81.
!True
!False

!False

!False

!Task 6
Постоянная времени звена, переходная функция которого представлена на следующем рисунке:
равен:
!Solution
Из
теории временных характеристик типовых
динамических звеньев известно, что
переходная функция консервативного
звена имеет вид:

![]() .
(коэффициент передачи консервативного
звена равен половине амплитуды).
.
(коэффициент передачи консервативного
звена равен половине амплитуды). ![]()
 (произведение равно полупериоду).
Следовательно,
(произведение равно полупериоду).
Следовательно, ![]() .
.
Правильный ответ:
Литература:
Бесекерский В.А., Попов Е.П. Теория систем автоматического управления. – Изд. 4-е, перераб. и доп. - СПб: Профессия, 2007 г. – с. 71-73.
!True
!False
![]()
!False
![]()
!False
![]()
!Task 7
Коэффициент передачи звена, переходная функция которого представлена на следующем рисунке:
равен:
!Solution
Из
теории временных характеристик типовых
динамических звеньев известно, что
переходная функция консервативного
звена имеет вид:
![]() .
(коэффициент передачи консервативного
звена равен половине амплитуды).
.
(коэффициент передачи консервативного
звена равен половине амплитуды).
![]() (произведение равно полупериоду).
Следовательно,
.
(произведение равно полупериоду).
Следовательно,
.
Правильный ответ:
Литература:
Бесекерский В.А., Попов Е.П. Теория систем автоматического управления. – Изд. 4-е, перераб. и доп. - СПб: Профессия, 2007 г. – с. 71-73.
!True
!False
!False
![]()
!False
![]()
!Task 8
Постоянная времени звена, переходная функция которого представлена на следующем рисунке:
равна:
!Solution
Из
теории временных характеристик типовых
динамических звеньев известно, что
переходная функция консервативного
звена имеет вид:
.
![]() (коэффициент передачи консервативного
звена равен половине амплитуды).
(коэффициент передачи консервативного
звена равен половине амплитуды).
![]() (произведение равно полупериоду).
Следовательно,
(произведение равно полупериоду).
Следовательно,
![]() .
.
Правильный ответ:
Литература:
Бесекерский В.А., Попов Е.П. Теория систем автоматического управления. – Изд. 4-е, перераб. и доп. - СПб: Профессия, 2007 г. – с. 71-73.
!True
!False
![]()
!False
![]()
!False
![]()
!Task 9
Коэффициент передачи звена, переходная функция которого представлена на следующем рисунке:
равен:
!Solution
Из теории временных характеристик типовых динамических звеньев известно, что переходная функция консервативного звена имеет вид: . (коэффициент передачи консервативного звена равен половине амплитуды). (произведение равно полупериоду). Следовательно, .
Правильный ответ:
Литература:
Бесекерский В.А., Попов Е.П. Теория систем автоматического управления. – Изд. 4-е, перераб. и доп. - СПб: Профессия, 2007 г. – с. 71-73.
!True
!False
![]()
!False
![]()
!False
![]()
!Task 10
Модуль звена постоянного запаздывания при частоте w = 1 равен …
!Solution
Частотная передаточная функция W(jw) представляет собой комплексное число, модуль которого равен отношению амплитуды выходной величины к амплитуде входной. У звена постоянного запаздывания выходная величина в точности повторяет входную, но с постоянным запаздыванием. Тогда модуль
A(w)=1.
Правильный ответ:
1.
Литература: 1.Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 55.
2. Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 79.
!True
1
!False
0
!False
∞
!False
0.5
!Task 11
Частотная передаточная функция звена, описываемого дифференциальным уравнением

имеет вид …
!Solution
Нужно перейти от дифференциального уравнения к передаточной функции звена.
Дифференциальные уравнения записываются так, чтобы выходная величина и её производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Считая условно оператор дифференцирования p=d/dt алгебраической величиной, решим данное уравнение относительно выходной величины. Полученное выражение представляет собой символическую запись дифференциального уравнения и вводиться для сокращения её записи. Более строго передаточная функция определяется через изображения Лапласа.
Если ввести изображения по Лапласу входных и выходных величин, где s=c+jw – комплексная величина, то передаточную функцию можно строго определить как отношение изображений выходной и входной величины звена при нулевых начальных условиях и равных нулю остальных воздействиях на звено.
В
данном случае передаточная функция
имеет вид
![]() .
Далее найдем частотную передаточную
функцию. Произведем замену s
на jw.
.
Далее найдем частотную передаточную
функцию. Произведем замену s
на jw.
Частотная передаточная функция может быть представлена в следующем виде:
![]()
Для нахождения вещественной и мнимой частей частотной передаточной функции необходимо освободиться от мнимости в знаменателе путем умножения числителя и знаменателя на комплексную величину, сопряженную знаменателю, и затем произвести разделение на вещественную и мнимую части.
Для данного звена получим:
![]() .
.
Правильный ответ: .
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 44-47.
!True

!False

!False
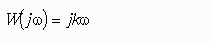
!False

!Task 12
Частотная передаточная функция звена, описываемого дифференциальным уравнением

имеет вид …
!Solution
Нужно перейти от дифференциального уравнения к передаточной функции звена.
Дифференциальные уравнения записываются так, чтобы выходная величина и её производные находились в левой части уравнения, а входная величина и все остальные члены - в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Считая условно оператор дифференцирования p=d/dt алгебраической величиной, решим данное уравнение относительно выходной величины. Полученное выражение представляет собой символическую запись дифференциального уравнения и вводиться для сокращения её записи. Более строго передаточная функция определяется через изображения Лапласа.
Если ввести изображения по Лапласу входных и выходных величин, где s=c+jw – комплексная величина, то передаточную функцию можно строго определить как отношение изображений выходной и входной величины звена при нулевых начальных условиях и равных нулю остальных воздействиях на звено.
В
данном случае передаточная функция
имеет вид
![]() .
Далее найдем частотную передаточную
функцию. Произведем замену s
на jw.
.
Далее найдем частотную передаточную
функцию. Произведем замену s
на jw.
Частотная передаточная функция может быть представлена в следующем виде:
Для нахождения вещественной и мнимой частей частотной передаточной функции необходимо освободиться от мнимости в знаменателе путем умножения числителя и знаменателя на комплексную величину, сопряженную знаменателю, и затем произвести разделение на вещественную и мнимую части.
Для данного звена получим:
![]() .
.
Правильный ответ: .
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 44-47.
!True
!False
!False
!False
!Task 13
Амплитудно-фазовая частотная характеристика звена с передаточной функцией
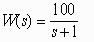
имеет вид …
!Solution
Амплитудно-фазовая частотная характеристика строится на комплексной плоскости. Она представляет собой геометрическое место концов векторов (годограф), соответствующих частотной передаточной функции. W(jw)=U(w)+jV(w) при изменении частоты от нуля до бесконечности.
Гораздо проще её строить, используя полярные координаты, т.е. вычисляя непосредственно модуль и фазу:
![]()
Зная их можно легко построить соответствующую точку на комплексной плоскости.
Модуль частотной передаточной функции находится как отношение модулей её числителя и знаменателя. Для апериодического звена 1 порядка в нашем случае будет иметь вид:
![]()
Фаза изменяется от 0 до –π/2. Таким образом, A(w) будет меняться от 100 до 0 при изменении w от 0 до ∞. Вся характеристика будет в четвертом квадранте.
Правильный
ответ:

Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 56,64-65.
!True
!False
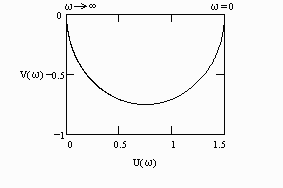
!False
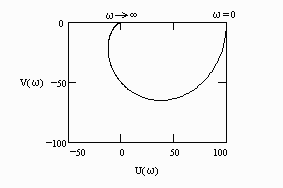
!False
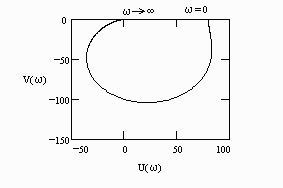
!Task 14
Амплитудно-фазовая частотная характеристика звена с передаточной функцией
![]()
имеет вид …
!Solution
Корни знаменателя являются комплексными числами, значит рассматриваемое звено является колебательным.
Амплитудно-фазовая частотная характеристика строится на комплексной плоскости. Она представляет собой геометрическое место концов векторов (годограф), соответствующих частотной передаточной функции. W(jw)=U(w)+jV(w) при изменении частоты от нуля до бесконечности.
Гораздо проще её строить, используя полярные координаты, т.е. вычисляя непосредственно модуль и фазу:
Зная их можно легко построить соответствующую точку на комплексной плоскости.
Модуль частотной передаточной функции находится как отношение модулей её числителя и знаменателя. Для апериодического звена 2-ого порядка в нашем случае будет иметь вид:

Фаза изменяется от 0 до –π. Таким образом, A(w) будет меняться от 100 до 0 при изменении w от 0 до ∞. Вся характеристика будет в четвертом и третьем квадрантах.
Правильный ответ:
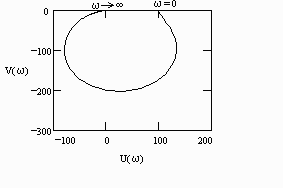 Литература:
Бесекерский В.А., Попов Е.П. Теория систем
автоматического управления.- СПб.
Профессия. 2007, 752 с., стр. 56.,64-65.
Литература:
Бесекерский В.А., Попов Е.П. Теория систем
автоматического управления.- СПб.
Профессия. 2007, 752 с., стр. 56.,64-65.
!True
!False
!False
!False
!Task 15
Амплитудно-фазовая частотная характеристика звена с передаточной функцией
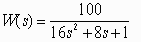
имеет вид …
!Solution
Корни знаменателя являются отрицательными вещественными числами, значит рассматриваемое звено является апериодическим 2-ого порядка.
Амплитудно-фазовая частотная характеристика строится на комплексной плоскости. Она представляет собой геометрическое место концов векторов (годограф), соответствующих частотной передаточной функции. W(jw)=U(w)+jV(w) при изменении частоты от нуля до бесконечности.
Гораздо проще её строить, используя полярные координаты, т.е. вычисляя непосредственно модуль и фазу:
Зная их можно легко построить соответствующую точку на комплексной плоскости.
Модуль частотной передаточной функции находится как отношение модулей её числителя и знаменателя. Для колебательного звена 2-ого порядка в нашем случае будет иметь вид:

Фаза изменяется от 0 до –π. Таким образом, A(w) будет меняться от 100 до 0 при изменении w от 0 до ∞. Вся характеристика будет в четвертом и третьем квадрантах.
Правильный ответ:
!True
!False
!False
!False
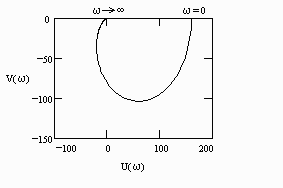
!Task 16
Вещественная часть частотной передаточной функции звена с передаточной
функцией
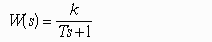
имеет вид …
!Solution
Частотная передаточная функция может быть представлена в следующем виде:
Для нахождения вещественной и мнимой частей частотной передаточной функции необходимо освободиться от мнимости в знаменателе путем умножения числителя и знаменателя на комплексную величину, сопряженную знаменателю, и затем произвести разделение на вещественную и мнимую части.
Правильный ответ:
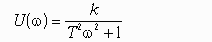
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб., Профессия. 2007, 752 с., стр. 55-56.
!True
!False
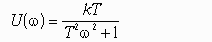
!False
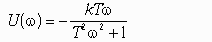
!False
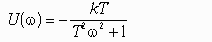
!Task 17
Мнимая часть частотной передаточной функции звена
имеет вид …
!Solution
Частотная передаточная функция может быть представлена в следующем виде:
Для нахождения вещественной и мнимой частей частотной передаточной функции необходимо освободиться от мнимости в знаменателе путем умножения числителя и знаменателя на комплексную величину, сопряженную знаменателю, и затем произвести разделение на вещественную и мнимую части.
Правильный ответ:
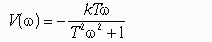
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб., Профессия. 2007, 752 с., стр. 55-56.
!True
!False
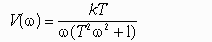
!False
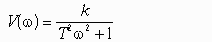
!False

!Task 18
Мнимая часть частотной передаточной функции звена

имеет вид …
!Solution
Частотная передаточная функция может быть представлена в следующем виде:
Для нахождения вещественной и мнимой частей частотной передаточной функции необходимо освободиться от мнимости в знаменателе путем умножения числителя и знаменателя на комплексную величину, сопряженную знаменателю, и затем произвести разделение на вещественную и мнимую части.
Правильный ответ:

Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб., Профессия. 2007, 752 с., стр. 55-56.
!True
!False
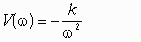
!False

!False

!Task 19
Модуль частотной передаточной функции звена
имеет вид …
!Solution
Частотная передаточная функция может быть представлена в следующем виде:
Модуль частотной передаточной функции данного звена находится как отношение модулей её числителя и знаменателя, для апериодического звена это будет:
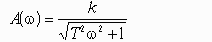
Правильный ответ:
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия., 2007, 752 с., стр. 55,65.
!True
!False
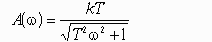
!False
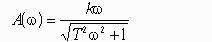
!False
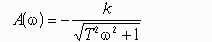
!Task 20
Модуль частотной передаточной функции звена
имеет вид …
!Solution
Частотная передаточная функция может быть представлена в следующем виде:
Модуль частотной передаточной функции данного звена находится как отношение модулей её числителя и знаменателя, для интегрирующего звена это будет:

Правильный ответ:
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия., 2007, 752 с., стр. 55,65.
!True
!False

!False
![]()
!False
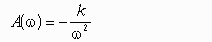
!Task 21
Наклон асимптотической логарифмической амплитудной частотной характеристики (ЛАЧХ) звена с передаточной функцией на частоте 30 1/с.
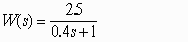
равен ______ дБ/дек.
!Solution
При возрастании w строим асимптотическую ЛАХ, как ломанную линию, прямолинейные отрезки которой изменяют наклон при сопрягающих частотах wi на ±20 дБ/дек, если wi – принадлежит звену первого порядка, ±40 дБ/дек – звену второго порядка и т.д. Здесь + соответствует форсирующему звену (числитель ПФ), а – - инерционному звену (знаменатель ПФ). В данном случае можно не определяя значений сопрягающих частот сказать, что максимальный наклон, который дает знаменатель ПФ апериодического звена первого порядка – -20 дБ/дек., низкочастотная часть до сопрягающей частоты имеет наклон 0 дБ/дек. В данном случае сопрягающей частотой является 2,5 1/с , начиная с которой наклон будет – 20 дБ/дек, в том числе и на частоте 30 1/с.
Правильный ответ: -20 дБ/дек
Литература: 1. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 44-47.
!True
-20
!False
+20
!False
-40
!False
+40
!Task 22
Наклон асимптотической логарифмической амплитудной частотной характеристики звена с передаточной функцией
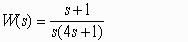
на частоте 1.5 1/с составит ______ дБ/дек.
!Solution
При возрастании w строим асимптотическую ЛАХ, как ломанную линию, прямолинейные отрезки которой изменяют наклон при сопрягающих частотах wi на ±20 дБ/дек, если wi – принадлежит звену первого порядка, ±40 дБ/дек – звену второго порядка и т.д. Здесь + соответствует форсирующему звену (числитель ПФ), а – - инерционному звену (знаменатель ПФ). В данном случае
сопрягающие частоты равны о,25 и 1 1/с, а заданная находится в высокочастотной части диапазона, где наклон ЛАЧХ составляет – 20дБ/дек.
Правильный ответ: -20 дБ/дек.
Литература: 1. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 44-47.
!True
-20
!False
+20
!False
-40
!False
+40
!Task 23
Наклон асимптотической логарифмической амплитудной частотной характеристики на частоте 0.2 1/с звена с передаточной функцией
составит _____ дБ/дек.
!Solution
При возрастании w строим асимптотическую ЛАХ, как ломанную линию, прямолинейные отрезки которой изменяют наклон при сопрягающих частотах wi на ±20 дБ/дек, если wi – принадлежит звену первого порядка, ±40 дБ/дек – звену второго порядка и т.д. Здесь + соответствует форсирующему звену (числитель ПФ), а – - инерционному звену (знаменатель ПФ). В данном случае cсопрягающая частота апериодического звена 1 –ого порядка равна 2,5 1/с, а значит на всех частотах меньше сопрягающей наклон равен 0 дБ/дек.
Правильный ответ: 0 дБ/дек
Литература: 1. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 44-47.
!True
0
!False
+20
!False
-40
!False
+40
!Task 24
Асимптотическая логарифмическая амплитудная частотная характеристика звена с передаточной функцией
![]()
проходит через точку, заданную координатами по оси абсцисс и оси ординат соответственно …
!Solution
Для построения ЛАХ используется стандартная сетка, где по оси абсцисс откладывается угловая частота в логарифмическом масштабе, т.е. наносятся отметки, соответствующие lgw. На оси ординат откладывается модуль (20lgk) в дБ. В данном случае асимптотическая ЛАЧХ проходи через точку на оси ординат 20lg100=40, а сопрягающая частота равна 10 1/с , на оси абсцисс это точка lg 10=1, т.е. точка с координатами 1, 40 принадлежит асипмтотической характеристики апериодического звена 1-ого порядка .
Правильный ответ: 1, 40.
Литература: 1. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр.58.
!True
1, 40
!False
10, 40
!False
0.1, 40
!False
10, 10
!Task 25
Асимптотическая логарифмическая амплитудная частотная характеристика звена с передаточной функцией
![]()
проходит через точку, заданную координатами по оси абсцисс и оси ординат соответственно …
!Solution
Для построения ЛАХ используется стандартная сетка, где по оси абсцисс откладывается угловая частота в логарифмическом масштабе, т.е. наносятся отметки, соответствующие lgw. На оси ординат откладывается модуль (20lgk) в дБ. В данном случае асимптотическая ЛАЧХ проходи через точку на оси ординат 20lg10=20, а сопрягающая частота равна 100 1/с , на оси абсцисс это точка lg 100=2, т.е. точка с координатами 2, 20 принадлежит асипмтотической характеристики апериодического звена 1-ого порядка.
Правильный ответ: 2, 20.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр.58.
!True
2,20
!False
2, -20
!False
0.1, 40
!False
1, 40
!Task 26
Значение фазового сдвига для звена с передаточной функцией

на частоте 2.5 1/c равно ______ угловых градусов.
!Solution
Частотные функции данного звена определяются формулами:
![]() ,
A(w)=
,
A(w)=![]() ,
,
а
фазовая характеристика во всём диапазоне
частот будет вносить фазовый сдвиг
равный -![]() .
.
Правильный ответ: -π/2 или -90 угловых градусов
Литература: Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 55.
!True
-90
!False
0
!False
-45
!False
-180
!Task 27
Значение фазового сдвига для звена с передаточной функцией
W(s)=0.2s на частоте 2.5 1/с равно ______ угловых градусов.
!Solution
Частотные функции дифференцирующего звена определяются формулами:
![]() ,
A(w)=kw,
,
A(w)=kw,
а фазовая характеристика во всём диапазоне частот будет вносить фазовый сдвиг равный + .
Правильный ответ: +π/2 или +90 угловых градусов
Литература: Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 55.
!True
90
!False
-90
!False
-45
!False
0
!Task 28
Значение фазового сдвига для звена с передаточной функцией
на частоте 100 1/c равно ______ угловых градусов.
!Solution
Фазовый сдвиг апериодического звена 1-го порялка определяется выражением (- arctg wT), т.е. если w=1/T, что имеет место в данном случае, то –arctg 1= -45
Правильный ответ: -45 угловых градусов
Литература: : Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр.64.
!True
-45
!False
-90
!False
90
!False
0
!Task 29
Значение фазового сдвига для звена с передаточной функцией
![]()
на частоте 2.5 1/с равно …
!Solution
Частотные функции данного звена определяются формулами:
, A(w)= ,
а фазовая характеристика во всём диапазоне частот будет вносить фазовый сдвиг равный - .
Правильный ответ: -π/2 или -90 угловых градусов
Литература: Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 55.
!True
-π/2
!False
+π/2
!False
-π
!False
+π
!Task 30
Значение фазового сдвига для звена с передаточной функцией
на частоте 2.5 1/с равно …
!Solution
Фазовый сдвиг апериодического звена 1-го порялка определяется выражением (- arctg wT), т.е. если w=1/T, что имеет место в данном случае, то –arctg 1= -45
Правильный ответ: -45 угловых градусов
Литература: : Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр.64.
!True
-π/4
!False
-π/2
!False
+π/4
!False
-π
!Task 31
Значение фазового сдвига для звена с передаточной функцией
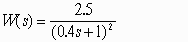
на частоте 2.5 1/с равно …
!Solution
Фазовый сдвиг апериодического звена 2-го порялка определяется выражением (- arctg wT1 - arctg wT2), в данном случае T1=T2 и если w=1/T, то суммарный фазовый сдвиг будет равен –arctg 1 – arctg 1= -90
Правильный ответ: -90 угловых градусов
Литература: : Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр.64.
!True
-π/2
!False
+π/2
!False
-π
!False
+π
!Task 32
Значение фазового сдвига для звена с передаточной функцией
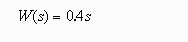
на частоте 2.5 1/с равно …
!Solution
Частотные функции дифференцирующего звена определяются формулами:
, A(w)=kw,
а фазовая характеристика во всём диапазоне частот будет вносить фазовый сдвиг равный + .
Правильный ответ: +π/2
Литература: Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 55.
!True
+π/2
!False
-π/2
!False
-π
!False
+π
!Task 33
Значение фазового сдвига для звена с передаточной функцией
на частоте 250 1/с будет стремится к …
!Solution
Фазовый сдвиг апериодического звена 2-го порялка определяется выражением (- arctg wT1 - arctg wT2), в данном случае T1=T2
Заданная частота на два порядка превышает сопрягающую частоту, значит фазовый сдвиг в этих условиях стремиться к – π (-180 градусов).
Правильный ответ: -180 угловых градусов
Литература: : Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр.64.
!True
-π
!False
-π/2
!False
+π
!False
+π/2
!Task 34
Резонансная частота звена с передаточной функцией
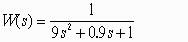
равна _____ 1/с.
!Solution
В соответствии с определением колебательного звена коэффициент при s2 равен T2, значит постоянная времени звена Т=3 с, а соответствующая резонансная частота равна 1/3 1/с.
Правильный ответ: 1/3 1/с.
Литература: : Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр.62.
!True
1/3
!False
0.1
!False
9.0
!False
0
!Task 35
Декремент затухания колебательного звена вида
![]()
будет равен …
!Solution
В соответствии с определением колебательного звена коэффициент при s2 равен T2, а коэффициент при s равен 2T£, где £ - декремент затухания. Тогда, если Т=0.5, то £=0,1.
Правильный ответ: 0,1
Литература: : Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр.62.
!True
0,1
!False
0.5
!False
1
!False
0,2
!Task 36
Фазовый сдвиг, вносимый колебательным звеном вида
на частоте 2 1/с, будет равен …
!Solution
Фазовый сдвиг, вносимый колебательным звеном, изменяется с частотой от 0 до –π, на резонансной частоте он равен – π/2.
Правильный ответ: – π/2
Литература: : Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр.62.
!True
-π/2
!False
+π/2
!False
-π
!False
+π
!Task 37
Фазовый сдвиг колебательного звена вида
на частоте 200 1/с будет стремиться к …
!Solution
Фазовый сдвиг, вносимый колебательным звеном, изменяется с частотой от 0 до –π, на резонансной частоте он равен – π/2. Заданная частота на два порядка выше резонансной, значит фазовый сдвиг будет стремиться к –π.
Правильный ответ: – π
Литература: : Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр.62.
!True
-π
!False
+π/2
!False
-π/2
!False
+π
!Task 38
Фазовый сдвиг колебательного звена вида
![]()
на частоте 2,5 1/с будет равен …
!Solution
В соответствии с определением колебательного звена коэффициент при s2 равен T2, значит 1/T=2,5 1/С. Т.е. заданная частота равна резонансной.
Фазовый сдвиг, вносимый колебательным звеном, изменяется с частотой от 0 до –π, на резонансной частоте он равен – π/2.
Правильный ответ: – π/2
Литература: : Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр.62.
!True
-π/2
!False
+π/2
!False
-π
!False
+π
!Task 39
Вероятность появления резонанса на амплитудно-частотной характеристике звена передаточной функцией вида
![]()
стремится к …
!Solution
Определим, является ли данное звено колебательным. Для этого найдём корни знаменателя. Они отрицательные вещественные и равны между собой, т.е. данное звено является апериодическим 2-ого порядка. Частотная характеристика такого звена не имеет резонанса. Т.е. вероятность его наличия равна 0.
Правильный ответ: 0.
Литература: : Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр.64-65.
!True
0
!False
1
!False
0,5
!False
0,75
!Task 40
На рисунке представлены логарифмические амплитудо-частотные и фазо-частотные характеристики звена …
!Solution
При возрастании w строим асимптотическую ЛАХ, как ломанную линию, прямолинейные отрезки которой изменяют наклон при сопрягающих частотах wi на ±20 дБ/дек, если wi – принадлежит звену первого порядка, ±40 дБ/дек – звену второго порядка и т.д. Здесь + соответствует форсирующему звену (числитель ПФ ), а – - инерционному звену (знаменатель ПФ). Таким образом, можно восстановить передаточную функцию: низкочастотная часть представляет идеальное дифференцирующее звено, а высокочастотная часть характеристики представлена апериодическим звеном первого порядка. Т.е. имеет вид:
![]() ,
что описывает дифференцирующее звено
с замедлением.
,
что описывает дифференцирующее звено
с замедлением.
Правильный ответ: дифференцирующего звена с замедлением
Литература: 1. Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления: Учебное пособие. – Ростов н/Д: Феникс, 2007. -469 с., стр. 88.

!True
дифференцирующего с замедлением
!False
идеального дифференцирующего
!False
изодромного
!False
интегрирующего с замедлением
!Task 41
Для построения амплитудно-фазо частотной характеристики (АФЧХ) используется частотная передаточная функция вида …
!Solution
Частотная передаточная функция может быть представлена в следующем виде:
![]()
где
A(w)
– модуль частотной передаточной функции,
![]() (w)
– аргумент, U(w)
и V(w)
– вещественная и мнимая составляющие
частотной передаточной функции.
(w)
– аргумент, U(w)
и V(w)
– вещественная и мнимая составляющие
частотной передаточной функции.
Модуль частотной передаточной функции находится как отношение модулей числителя и знаменателя.
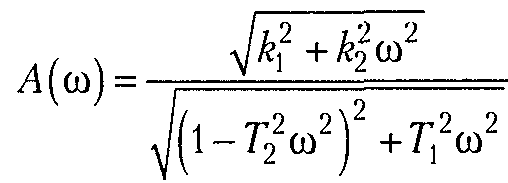
Аргумент или фаза частотной передаточной функции находится как разность аргументов числителя и знаменателя.
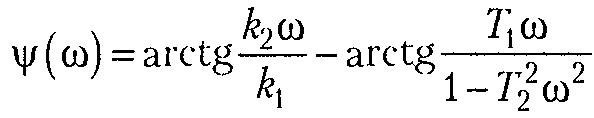
Для нахождения вещественной и мнимой частей частотной передаточной функции необходимо освободиться от мнимости в знаменателе путем умножения числителя и знаменателя на комплексную величину, сопряженную знаменателю, и затем произвести разделение на вещественную и мнимую части.
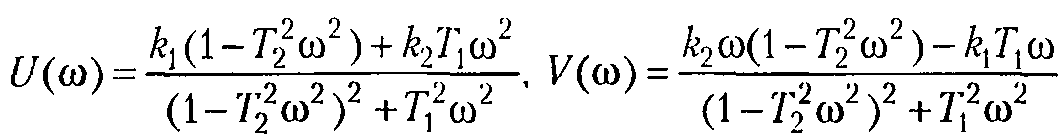
Правильный
ответ:
![]()
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с.,стр. 53-85.
!True
!False
![]()
!False
![]()
!False
![]()
!Task 42
Вещественную часть частотной передаточной функции звена
![]()
выглядит так
!Solution
Частотная передаточная функция может быть представлена в следующем виде:
где A(w) – модуль частотной передаточной функции, (w) – аргумент, U(w) и V(w) – вещественная и мнимая составляющие частотной передаточной функции.
Модуль частотной передаточной функции находится как отношение модулей числителя и знаменателя. Аргумент или фаза частотной передаточной функции находится как разность аргументов числителя и знаменателя. Для нахождения вещественной и мнимой частей частотной передаточной функции необходимо освободиться от мнимости в знаменателе путем умножения числителя и знаменателя на комплексную величину, сопряженную знаменателю, и затем произвести разделение на вещественную и мнимую части.
Правильный
ответ:
![]()
Литература:Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с.,стр. 53-85.
!True
!False
![]()
!False
![]()
!False
![]()
!END
*********************************************
*ОТУ 1.2.04.t2.rtf
*********************************************
!Taskfile ОТУ 1.2.04.#Структурные преобразования систем
!DE=ОТУ 1.2.#Структурные представления систем управления
!Type=2
!Time=2
Экспертные и технологические параметры заданий:
1. Дисциплина: Основы теории управления
2. Объем часов: группа I (от 80 до 170 часов)
3. Дидактическая единица ГОС: Структурные представления систем управления
4. Тема задания: Структурные преобразования систем
5. Уровень сложности: 2 (знать и уметь использовать в типовой учебной ситуации)
6. Ориентировочное время выполнения: 2 минуты
7. Перечень контролируемых учебных элементов
Студент должен знать: принципы построения структурных схем
уметь: применять правила структурных преобразований систем
8. Форма заданий: выбор одного ответа из четырех предложенных
!Task 1
Если H1(s)=5 - передаточная функция прямой связи, а H2(s)=3/s - передаточная функция отрицательной обратной связи, то результирующая передаточная функция будет определяться выражением …
!Solution
Пусть W1(s) – передаточная функция звена в прямой цепи, а W2(s) – звено в обратной связи, а обратная связь может быть как положительной, так и отрицательной. Тогда результирующую передаточную функцию можно найти по формуле:
Здесь знак минус относится к положительной, а знак плюс - к отрицательной обратной связи.
Правильный
ответ:

Литература: 1. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 93.
!True

!False

!False

!False

!Task 2
Если H1(s)=2 - передаточная функция прямой связи, а H2(s)=1/s - передаточная функция отрицательной обратной связи, то результирующая передаточная функция будет определяться выражением …
!Solution
Пусть W1(s) – передаточная функция звена в прямой цепи, а W2(s) – звено в обратной связи, а обратная связь может быть как положительной, так и отрицательной. Тогда результирующую передаточную функцию можно найти по формуле:
Здесь знак минус относится к положительной, а знак плюс - к отрицательной обратной связи.
Правильный
ответ:

Литература: 1. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 93.
!True
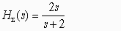
!False

!False

!False

!Task 3
Если H1(s)=2 - передаточная функция прямой связи, а H2(s)=1/s+1 - передаточная функция отрицательной обратной связи, то результирующая передаточная функция будет определяться выражением …
!Solution
Пусть W1(s) – передаточная функция звена в прямой цепи, а W2(s) – звено в обратной связи, а обратная связь может быть как положительной, так и отрицательной. Тогда результирующую передаточную функцию можно найти по формуле:
Здесь знак минус относится к положительной, а знак плюс - к отрицательной обратной связи.
Правильный ответ:

Литература: 1. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 93.
!True
!False

!False

!False

!Task 4
При параллельном соединении двух звеньев с передаточными функциями H(s)=2/s и H(s)=3/(s+1) результирующая передаточная функция будет иметь вид …
!Solution
При параллельном соединении звеньев результирующая передаточная функция будет равна сумме всех передаточных функций звеньев, при отсутствии взаимного влияния звеньев друг на друга:

Правильный
ответ:

Литература: 1. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 92.
!True

!False

!False

!False

!Task 5
При параллельном соединении двух звеньев с передаточными функциями H(s)=2s и H(s)=4/(s+2) результирующая передаточная функция будет иметь вид …
!Solution
При параллельном соединении звеньев результирующая передаточная функция будет равна сумме передаточных функций всех звеньев, при отсутствии взаимного влияния звеньев друг на друга:
Правильный
ответ:

Литература: 1. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 92.
!True

!False

!False

!False

!Task 6
При параллельном соединении двух звеньев с передаточными функциями H(s)=2s и H(s)=5 результирующая передаточная функция будет иметь вид …
!Solution
При параллельном соединении звеньев результирующая передаточная функция будет равна сумме передаточных функций всех звеньев, при отсутствии взаимного влияния звеньев друг на друга:
Правильный
ответ:

Литература: 1. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 92.
!True

!False

!False

!False
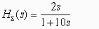
!Task 7
При параллельном соединении двух звеньев с передаточными функциями H(s)=2/(s+3) и H(s)=3/(s+5) результирующая передаточная функция будет иметь вид …
!Solution
При параллельном соединении звеньев результирующая передаточная функция будет равна сумме передаточных функций всех звеньев, при отсутствии взаимного влияния звеньев друг на друга:
Правильный
ответ:

Литература: 1. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 92.
!True
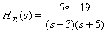
!False
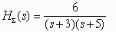
!False

!False

!Task 8
При параллельном соединении двух звеньев с передаточными функциями H(s)=2/s и H(s)=5 результирующая передаточная функция будет иметь вид …
!Solution
При параллельном соединении звеньев результирующая передаточная функция будет равна сумме передаточных функций всех звеньев, при отсутствии взаимного влияния звеньев друг на друга:
Правильный
ответ:

Литература: 1. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 92.
!True
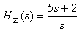
!False
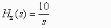
!False

!False

!Task 9
При параллельном соединении двух звеньев с передаточными функциями H(s)=2 и H(s)=5/(s+1) результирующая передаточная функция будет иметь вид …
!Solution
При параллельном соединении звеньев результирующая передаточная функция будет равна сумме передаточных функций всех звеньев, при отсутствии взаимного влияния звеньев друг на друга:
Правильный
ответ:
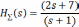
Литература: 1. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 92.
!True
!False

!False

!False

!Task 10
При последовательном соединении двух звеньев с передаточными функциями H(s)=2/s и H(s)=3/(s+1) результирующая передаточная функция будет иметь вид …
!Solution
При последовательном соединении звеньев результирующая передаточная функция будет равна произведению передаточных функций всех звеньев, при отсутствии взаимного влияния звеньев друг на друга:
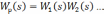
Правильный
ответ:
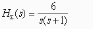
Литература: 1. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 92.
!True

!False

!False

!False

!Task 11
При последовательном соединении двух звеньев с передаточными функциями H(s)=2s и H(s)=4/(s+2) результирующая передаточная функция будет иметь вид …
!Solution
При последовательном соединении звеньев результирующая передаточная функция будет равна произведению передаточных функций всех звеньев, при отсутствии взаимного влияния звеньев друг на друга:
Правильный
ответ:

Литература: 1. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 92.
!True
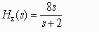
!False

!False

!False

!Task 12
При последовательном соединении двух звеньев с передаточными функциями H(s)=2s и H(s)=5 результирующая передаточная функция будет иметь вид …
!Solution
При последовательном соединении звеньев результирующая передаточная функция будет равна произведению передаточных функций всех звеньев, при отсутствии взаимного влияния звеньев друг на друга:
Правильный
ответ:

Литература: 1. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 92.
!True

!False

!False

!False

!Task 13
При последовательном соединении двух звеньев с передаточными функциями H(s)=2/(s+3) и H(s)=3/(s+5) результирующая передаточная функция будет иметь вид …
!Solution
При последовательном соединении звеньев результирующая передаточная функция будет равна произведению передаточных функций всех звеньев, при отсутствии взаимного влияния звеньев друг на друга:
Правильный
ответ:

Литература: 1. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 92.
!True
!False

!False

!False

!Task 14
При последовательном соединении двух звеньев с передаточными функциями H(s)=2/s и H(s)=5 результирующая передаточная функция будет иметь вид …
!Solution
При последовательном соединении звеньев результирующая передаточная функция будет равна произведению передаточных функций всех звеньев, при отсутствии взаимного влияния звеньев друг на друга:
Правильный
ответ:

Литература: 1. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 92.
!True
!False

!False
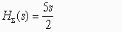
!False

!Task 15
При последовательном соединении двух звеньев с передаточными функциями H(s)=10/(s+3) и H(s)=5/(s+5) результирующая передаточная функция будет иметь вид …
!Solution
При последовательном соединении звеньев результирующая передаточная функция будет равна произведению передаточных функций всех звеньев, при отсутствии взаимного влияния звеньев друг на друга:
Правильный
ответ:

Литература: 1. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 92.
!True
!False

!False

!False
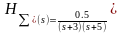
!Task 16
При переносе узла с входа на выход звена исходная схема

преобразуется следующим образом …
!Solution
Правила преобразования структурных и линейных схем.
Правильный
ответ:

Литература: 1. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 96.
!True

!False
!False

!False

!Task 17
При переносе узла с выхода на вход звена исходная схема
преобразуется следующим образом …
!Solution
Правила преобразования структурных и линейных схем.
Правильный
ответ:

Литература: 1. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 96.
!True
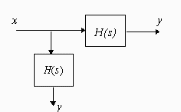
!False

!False

!False

!Task 18
При переносе сумматора с входа на выход звена исходная схема

преобразуется следующим образом …
!Solution
Правила преобразования структурных и линейных схем.
Правильный
ответ:

Литература: 1. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 96.
!True

!False

!False

!False

!Task 19
При переносе сумматора с выхода на вход звена исходная схема

преобразуется следующим образом …
!Solution
Правила преобразования структурных и линейных схем.
Правильный
ответ:

Литература: 1. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 96.
!True
!False

!False

!False

!END
*********************************************
*ОТУ 1.3.01.t2.rtf
*********************************************
!Taskfile ОТУ 1.3.01.#Корневые методы исследования устойчивости линейных систем
!DE=ОТУ 1.3.#Устойчивость непрерывных систем управления
!Type=2
!Time=2
Экспертные и технологические параметры заданий:
1. Дисциплина: Основы теории управления
2. Объем часов: группа I (от 80 до 170 часов)
3. Дидактическая единица ГОС: Устойчивость непрерывных систем управления
4. Тема задания: Корневые методы исследования устойчивости линейных систем
5. Уровень сложности: 2 (знать и уметь использовать в типовой учебной ситуации)
6. Ориентировочное время выполнения: 2 минуты
7. Перечень контролируемых учебных элементов
Студент должен знать: необходимые и достаточные корневые условия устойчивости линейных непрерывных систем
уметь: использовать корневые методы для исследования устойчивости систем
8. Форма заданий: выбор одного ответа из четырех предложенных
!Task 1
Устойчивость линейной динамической системы может быть определена по характеру …
!Solution
Решение линейного дифференциального уравнения, описывающего процессы в динамической системе, ищется в виде суммы общего решения однородного и частного решения неоднородного уравнения. Общее решение однородного уравнения при учете начальных условий характеризует свободное движение системы. Частное решение неоднородного уравнения характеризует вынужденное движение системы. Устойчивость линейной системы определяется по характеру свободного движения.
Правильный ответ: свободного движения.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 118.
Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл.
!True
свободного движения
!False
вынужденного движения
!False
установившегося движения
!False
возмущенного движения
!Task 2
Если yo(t) - общее решение линейного однородного уравнения, описывающего поведение системы, и

то такая система …
!Solution
Решение линейного дифференциального уравнения, описывающего процессы в динамической системе, ищется в виде суммы общего решения однородного и частного решения неоднородного уравнения. Общее решение однородного уравнения при учете начальных условий характеризует свободное движение системы. Частное решение неоднородного уравнения характеризует вынужденное движение системы.
Устойчивость линейной системы определяется по характеру свободного движения. Если свободное движение стремится к нулю при t→ , то такая система является асимптотически устойчивой.
Правильный ответ: асимптотически устойчива.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 119.
Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл., стр. 145
!True
асимптотически устойчива
!False
нейтрально устойчива
!False
на границе устойчивости
!False
неустойчива
!Task 3
Переходная составляющая решения дифференциального уравнения, описывающего поведение линейной системы, имеет вид
уп(t) = C1exp(α1t) + C2exp(α2t) +...+ Ckexp(αkt),
где: Сi, αi - вещественные числа, i = 1...k; t - время. Необходимым и достаточным условием устойчивости такой системы является условие …
!Solution
Решение линейного дифференциального уравнения, описывающего процессы в динамической системе, ищется в виде суммы общего решения однородного и частного решения неоднородного уравнения. Общее решение однородного уравнения при учете начальных условий характеризует свободное движение системы. Частное решение неоднородного уравнения характеризует вынужденное движение системы.
Устойчивость линейной системы определяется по характеру свободного движения. Если свободное движение стремится к нулю при t→ , то такая система является асимптотически устойчивой. Для этого необходимо и достаточно, чтобы все функции exp(αit) стремились к нулю при t→, т.е. вещественные части αi были отрицательные.
В данном случае αi - вещественные числа, поэтому требуется, чтобы αi<0, i = 0,...,k.
Правильный ответ: αi<0, i = 0,...,k.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 119.
Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл., стр. 145
!True
αi<0, i = 0,...,k
!False
Ci<0, i = 0,...,k
!False
|αi| <1, i = 0,...,k
!False
|Ci| <1, i = 0,...,k
!Task 4
Переходная составляющая решения дифференциального уравнения, описывающего поведение линейной системы, имеет вид
уп(t) = C1exp(αt) + C2exp(β1t) +...+ C3exp(β2t),
где: С1, С2, С3 , α - вещественные числа; β1, β2 - комплексно сопряженные числа; t - время. Необходимым и достаточным условием устойчивости такой системы является условие
!Solution
Решение линейного дифференциального уравнения, описывающего процессы в динамической системе, ищется в виде суммы общего решения однородного и частного решения неоднородного уравнения. Общее решение однородного уравнения при учете начальных условий характеризует свободное движение системы. Частное решение неоднородного уравнения характеризует вынужденное движение системы.
Устойчивость линейной системы определяется по характеру свободного движения. Если свободное движение стремится к нулю при t→ , то такая система является асимптотически устойчивой. Для этого необходимо и достаточно, чтобы все функции exp(αit) стремились к нулю при t→, т.е. вещественные части αi были отрицательные.
В данном случае α - вещественное число, βi - комплексные, поэтому требуется, чтобы α<0 и Re β1 <0.
Правильный ответ: α<0 и Re β1 <0.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 119.
Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл., стр. 145
!True
α<0 и Re β1 <0.
!False
Ci < 0 , i = 1, 2, 3.
!False
|α|<1 и Re β1 <1.
!False
|Ci| < 0 , i = 1, 2, 3.
!Task 5
Расположение корней характеристического уравнения замкнутой системы показано на рисунке.

Автоматическая система …
!Solution
Устойчивость линейной системы определяется по характеру свободного движения. Если свободное движение стремится к нулю при t→ , то такая система является асимптотически устойчивой. Для этого необходимо и достаточно, все корни характеристического уравнения замкнутой системы имели отрицательные вещественные части.
В данном случае один вещественный корень больше нуля. Поэтому система неустойчива.
Правильный ответ: неустойчива.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 120.
Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл., стр. 145
!True
неустойчива
!False
устойчива
!False
на колебательной границе устойчивости
!False
на апериодической границе устойчивости
!Task 6
Расположение корней характеристического уравнения замкнутой системы показано на рисунке.

Автоматическая система …
!Solution
Устойчивость линейной системы определяется по характеру свободного движения. Если свободное движение стремится к нулю при t→ , то такая система является асимптотически устойчивой. Для этого необходимо и достаточно, все корни характеристического уравнения замкнутой системы имели отрицательные вещественные части.
В данном случае один вещественный корень больше нуля. Поэтому система устойчива.
Правильный ответ: устойчива.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 120.
Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл., стр. 145
!True
устойчива
!False
неустойчива
!False
на колебательной границе устойчивости
!False
на апериодической границе устойчивости
!Task 7
Расположение корней характеристического уравнения замкнутой системы показано на рисунке.
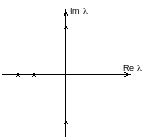
Автоматическая система …
!Solution
Устойчивость линейной системы определяется по характеру свободного движения. Если свободное движение стремится к нулю при t→ , то такая система является асимптотически устойчивой. Для этого необходимо и достаточно, все корни характеристического уравнения замкнутой системы имели отрицательные вещественные части.
В данном случае пара комплексно сопряженных корней имеет нулевую вещественную часть. Поэтому система находится на колебательной границе устойчивости.
Правильный ответ: на колебательной границе устойчивости.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 121.
Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл., стр. 145
!True
на колебательной границе устойчивости
!False
устойчива
!False
неустойчива
!False
на апериодической границе устойчивости
!Task 8
Расположение корней характеристического уравнения замкнутой системы показано на рисунке.

Автоматическая система …
!Solution
Устойчивость линейной системы определяется по характеру свободного движения. Если свободное движение стремится к нулю при t→ , то такая система является асимптотически устойчивой. Для этого необходимо и достаточно, все корни характеристического уравнения замкнутой системы имели отрицательные вещественные части.
В данном случае вещественный корень равен нулю. Поэтому система находится на апериодической границе устойчивости.
Правильный ответ: на границе устойчивости нейтрального типа.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 121.
Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл., стр. 145
!True
на границе устойчивости нейтрального типа
!False
устойчива
!False
неустойчива
!False
на колебательной границе устойчивости
!Task 9
Движение системы описывается дифференциальным уравнением

где: y(t) - выходная переменная, g(t) - задающее воздействие, t - время.
Автоматическая система …
!Solution
Устойчивость линейной системы определяется по характеру свободного движения. Если свободное движение стремится к нулю при t→ , то такая система является асимптотически устойчивой. Для этого необходимо и достаточно, все корни характеристического уравнения замкнутой системы имели отрицательные вещественные части.
В данном случае характеристическое уравнение имеет вид
λ2 + 3λ + 2 = 0,
корни уравнения λ1 = -1, λ2 = -2. Так как корни характеристического уравнения отрицательные, то система устойчива.
Правильный ответ: устойчива.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 120.
Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл., стр. 145
!True
устойчива
!False
неустойчива
!False
на колебательной границе устойчивости
!False
на апериодической границе устойчивости
!Task 10
Движение системы описывается дифференциальным уравнением

где: y(t) - выходная переменная, g(t) - задающее воздействие, t - время.
Автоматическая система …
!Solution
Устойчивость линейной системы определяется по характеру свободного движения. Если свободное движение стремится к нулю при t→ , то такая система является асимптотически устойчивой. Для этого необходимо и достаточно, все корни характеристического уравнения замкнутой системы имели отрицательные вещественные части.
В данном случае характеристическое уравнение имеет вид
λ2 + 1 = 0,
корни уравнения λ1,2 = ±j1. Так как корни характеристического уравнения комплексно сопряженные и имеют нулевую вещественную часть , то система находится на колебательной границе устойчивости.
Правильный ответ: на колебательной границе устойчивости.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 120.
Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл., стр. 145
!True
на колебательной границе устойчивости
!False
на апериодической границе устойчивости
!False
устойчива
!False
неустойчива
!Task 11
Движение системы описывается дифференциальным уравнением

где: y(t) - выходная переменная, g(t) - задающее воздействие, t - время.
Автоматическая система будет находиться на границе устойчивости при …
!Solution
Устойчивость линейной системы определяется по характеру свободного движения. Если свободное движение стремится к нулю при t→ , то такая система является асимптотически устойчивой. Для этого необходимо и достаточно, все корни характеристического уравнения замкнутой системы имели отрицательные вещественные части.
В данном случае характеристическое уравнение имеет вид
λ2 + А = 0.
При А ≤ 0 корни уравнения λ1,2 = ±√А, система неустойчива. При А > 0 корни уравнения λ1,2 = ±j√А, имеют нулевую вещественную часть, т.е.система находится на границе устойчивости.
Правильный ответ: А > 0.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 120.
Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл., стр. 145
!True
А > 0
!False
А ≤ 0
!False
А ≠0
!False
любом А
!Task 12
Движение системы описывается дифференциальным уравнением

где: y(t) - выходная переменная, g(t) - задающее воздействие, t - время.
Автоматическая система …
!Solution
Устойчивость линейной системы определяется по характеру свободного движения. Если свободное движение стремится к нулю при t→ , то такая система является асимптотически устойчивой. Для этого необходимо и достаточно, все корни характеристического уравнения замкнутой системы имели отрицательные вещественные части.
В данном случае характеристическое уравнение имеет вид
λ2 + 3λ = 0,
корни уравнения λ1 = 0 и λ2 = -3. Так как один их вещественных корней характеристического уравнения равен нулю, то система находится на апериодической границе устойчивости.
Правильный ответ: на границе устойчивости нейтрального типа.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 120.
Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл., стр. 145
!True
на границе устойчивости нейтрального типа
!False
на колебательной границе устойчивости
!False
устойчива
!False
неустойчива
!Task 13
Передаточная функция замкнутой системы имеет вид

Замкнутая система …
!Solution
Устойчивость линейной системы определяется по характеру свободного движения. Если свободное движение стремится к нулю при t→ , то такая система является асимптотически устойчивой. Для этого необходимо и достаточно, все корни характеристического уравнения замкнутой системы имели отрицательные вещественные части.
В данном случае характеристическое уравнение имеет вид
λ2 + 4λ+3 = 0,
корни уравнения λ1 = -1 и λ2 = -3. Так как вещественные корни характеристического уравнения отрицательные, то система устойчива.
Правильный ответ: устойчива.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 200.
Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл., стр. 145
!True
устойчива
!False
неустойчива
!False
на границе устойчивости нейтрального типа
!False
на колебательной границе устойчивости
!Task 14
Передаточная функция разомкнутой системы имеет вид

При замыкании отрицательной обратной связью система будет …
!Solution
Устойчивость линейной системы определяется по характеру свободного движения. Если свободное движение стремится к нулю при t→ , то такая система является асимптотически устойчивой. Для этого необходимо и достаточно, все корни характеристического уравнения замкнутой системы имели отрицательные вещественные части.
Передаточная функция замкнутой системы с отрицательной обратной связью равна

Характеристическое уравнение замкнутой системы имеет вид
λ2 + 10 = 0,
корни уравнения комплексные ( λ1,2 = ±j√10 ) и имеют нулевую вещественную часть, т.е.система находится на колебательной границе устойчивости.
Правильный ответ: на колебательной границе устойчивости.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 121.
Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл., стр. 145
!True
на колебательной границе устойчивости
!False
неустойчива
!False
на границе устойчивости нейтрального типа
!False
устойчива
!Task 15
Передаточная функция разомкнутой системы имеет вид

Замкнутая отрицательной обратной связью система будет устойчивой при значениях коэффициента передачи …
!Solution
Устойчивость линейной системы определяется по характеру свободного движения. Если свободное движение стремится к нулю при t→ , то такая система является асимптотически устойчивой. Для этого необходимо и достаточно, все корни характеристического уравнения замкнутой системы имели отрицательные вещественные части.
Передаточная функция замкнутой системы с отрицательной обратной связью равна
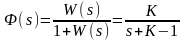
Характеристическое уравнение замкнутой системы имеет вид
λ + К-1 = 0,
корень уравнения вещественный, равный λ = -К+1. Корень системы будет отрицательным и система будет устойчива при К > 1.
Правильный ответ: К > 1.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 121.
Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл., стр. 145
!True
К > 1
!False
K < - 1
!False
|K| < 1
!False
К > 0
!Task 16
Передаточная функция разомкнутой системы имеет вид

Замкнутая неединичной отрицательной обратной связью с коэффициентом передачи Ко =2 система будет устойчивой при значениях коэффициента передачи …
!Solution
Устойчивость линейной системы определяется по характеру свободного движения. Если свободное движение стремится к нулю при t→ , то такая система является асимптотически устойчивой. Для этого необходимо и достаточно, все корни характеристического уравнения замкнутой системы имели отрицательные вещественные части.
Передаточная функция замкнутой системы с отрицательной обратной связью равна

Характеристическое уравнение замкнутой системы имеет вид
λ + 2К-4 = 0,
корень уравнения вещественный, равный λ = -2К+4. Корень системы будет отрицательным и система будет устойчива при К > 2.
Правильный ответ: К > 2.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 121.
Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл., стр. 145
!True
К > 2
!False
K < 2
!False
|K| < 2
!False
К > 0
!Task 17
Передаточная функция разомкнутой системы имеет вид

Замкнутая единичной отрицательной обратной связью система будет на границе устойчивости апериодического типа при значении коэффициента передачи …
!Solution
Устойчивость линейной системы определяется по характеру свободного движения. Если свободное движение стремится к нулю при t→ , то такая система является асимптотически устойчивой. Для этого необходимо и достаточно, все корни характеристического уравнения замкнутой системы имели отрицательные вещественные части.
Передаточная функция замкнутой системы с отрицательной обратной связью равна

Характеристическое уравнение замкнутой системы имеет вид
λ2 + 4λ +5+К = 0.
Система будет на границе устойчивости апериодического типа, когда один из двух вещественных корней будет равен нулю. Для этого необходимо положить 5 + К = 0, откуда получаем К = -5.
Правильный ответ: К = -5.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 121.
Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл., стр. 145
!True
К = -5
!False
K = 5
!False
K = -4
!False
К = -0,8
!Task 18
Передаточная функция замкнутой системы имеет вид

Переходной процесс системы будет сходящимся и носить колебательный характер при значениях коэффициента передачи
!Solution
Устойчивость линейной системы определяется по характеру свободного движения. Если свободное движение стремится к нулю при t→ , то такая система является асимптотически устойчивой. Для этого необходимо и достаточно, все корни характеристического уравнения замкнутой системы имели отрицательные вещественные части.
Переходной процесс в устойчивой системе сходится к установившемуся решению. Он носит колебательный характер, если корни характеристического уравнения комплексно сопряженные. Таким образом, по условию задачи необходимо найти значения К, при которых корни характеристического уравнения комплексно сопряженные и имеют отрицательную вещественную часть.
Характеристическое уравнение замкнутой системы имеет вид
λ2 + 4λ +К = 0.
Корни уравнения определяются по формуле
λ1,2 = -2 ±√(4 - К).
Система будет иметь два комплексно сопряженных корня с отрицательной вещественной частью, когда К > 4.
Правильный ответ: К > 4.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 121.
Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл., стр. 145
!True
К > 4
!False
K > 2
!False
K < 0
!False
К = 0
!Task 19
Передаточная функция замкнутой системы имеет вид

Переходной процесс системы будет сходящимся и носить апериодический характер при значениях коэффициента передачи …
!Solution
Устойчивость линейной системы определяется по характеру свободного движения. Если свободное движение стремится к нулю при t→ , то такая система является асимптотически устойчивой. Для этого необходимо и достаточно, все корни характеристического уравнения замкнутой системы имели отрицательные вещественные части.
Переходной процесс в устойчивой системе сходится к установившемуся решению. Он носит апериодический характер, если корни характеристического уравнения отрицательные вещественные. Таким образом, по условию задачи необходимо найти значения К, при которых корни характеристического уравнения различные и отрицательные.
Характеристическое уравнение замкнутой системы имеет вид
λ2 + 10λ +К = 0.
Корни уравнения определяются по формуле
λ1,2 = -5 ±√(25-К).
Система будет иметь два отрицательных вещественных корня, когда 0 < К < 25.
Правильный ответ: 0 < К < 25.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 121.
Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл., стр. 145
!True
0 < К < 25
!False
0 < К < 10
!False
|K| < 10
!False
К > 0
!Task 20
Передаточная функция разомкнутой системы имеет вид

При замыкании единичной положительной обратной связью система будет …
!Solution
Устойчивость линейной системы определяется по характеру свободного движения. Если свободное движение стремится к нулю при t→ , то такая система является асимптотически устойчивой. Для этого необходимо и достаточно, все корни характеристического уравнения замкнутой системы имели отрицательные вещественные части.
Передаточная функция замкнутой системы с положительной обратной связью равна

Характеристическое уравнение замкнутой системы имеет вид
λ - 10 = 0,
корень уравнения вещественный и положительный. Система неустойчива.
Правильный ответ: неустойчива.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 120.
Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл., стр. 145
!True
неустойчива
!False
устойчива
!False
на апериодической границе устойчивости
!False
на колебательной границе устойчивости
!Task 21
Передаточная функция разомкнутой системы имеет вид

При замыкании единичной положительной обратной связью система будет …
!Solution
Устойчивость линейной системы определяется по характеру свободного движения. Если свободное движение стремится к нулю при t→ , то такая система является асимптотически устойчивой. Для этого необходимо и достаточно, все корни характеристического уравнения замкнутой системы имели отрицательные вещественные части.
Передаточная функция замкнутой системы с положительной обратной связью равна

Характеристическое уравнение замкнутой системы имеет вид
0,1λ - 9 = 0,
корень уравнения вещественный и положительный. Система неустойчива. Правильный ответ: неустойчива.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 120.
Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл., стр. 145
!True
неустойчива
!False
устойчива
!False
на апериодической границе устойчивости
!False
на колебательной границе устойчивости
!Task 22
Передаточная функция разомкнутой системы имеет вид

Замкнутая единичной отрицательной обратной связью система будет на границе устойчивости колебательного типа при значении коэффициента передачи …
!Solution
Устойчивость линейной системы определяется по характеру свободного движения. Если свободное движение стремится к нулю при t→ , то такая система является асимптотически устойчивой. Для этого необходимо и достаточно, все корни характеристического уравнения замкнутой системы имели отрицательные вещественные части.
Передаточная функция замкнутой системы с отрицательной обратной связью равна

Характеристическое уравнение замкнутой системы имеет вид
λ2 + (4+К)λ +5 = 0.
Система будет на границе устойчивости колебательного типа, когда корни будут комплексно сопряженными с вещественной частью, равной нулю. Для этого необходимо положить 4 + К = 0, откуда получаем К = -4.
Правильный ответ: К = -4.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 121.
Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл., стр. 145
!True
К = -4
!False
K = 5
!False
K = -5
!False
К = 4
!Task 23
Для управления неустойчивым объектом используется пропорциональный регулятор, как показано на рисунке

Переходной процесс замкнутой системы будет сходящимся и носить апериодический характер при настройке регулятора …
!Solution
Устойчивость линейной системы определяется по характеру свободного движения. Если свободное движение стремится к нулю при t→ , то такая система является асимптотически устойчивой. Для этого необходимо и достаточно, все корни характеристического уравнения замкнутой системы имели отрицательные вещественные части.
Переходной процесс в устойчивой системе сходится к установившемуся решению. Он носит апериодический характер, если корни характеристического уравнения отрицательные вещественные. Таким образом, по условию задачи необходимо найти значения Кр , при которых корень характеристического уравнения отрицательный.
Характеристическое уравнение замкнутой системы имеет вид
λ -1 + 10Кр = 0.
Корень уравнения определяются по формуле
λ1 = 1 - 10Кр.
Система будет иметь отрицательный вещественный корень, если Кр > 0,1.
Правильный ответ: К > 0,1.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 121.
Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл., стр. 145
!True
Кр > 0,1
!False
Кр > 1
!False
Kр > 10
!False
Кр > 0
!Task 24
Для управления объектом, описываем интегрирующим звеном, используется пропорциональный регулятор, как показано на рисунке
Переходной процесс замкнутой системы будет сходящимся и носить апериодический характер при настройке регулятора
!Solution
Устойчивость линейной системы определяется по характеру свободного движения. Если свободное движение стремится к нулю при t→ , то такая система является асимптотически устойчивой. Для этого необходимо и достаточно, все корни характеристического уравнения замкнутой системы имели отрицательные вещественные части.
Переходной процесс в устойчивой системе сходится к установившемуся решению. Он носит апериодический характер, если корни характеристического уравнения отрицательные вещественные. Таким образом, по условию задачи необходимо найти значения Кр , при которых корень характеристического уравнения отрицательный.
Характеристическое уравнение замкнутой системы имеет вид
λ + 5Кр = 0.
Корень уравнения определяются по формуле
λ1 = - 5Кр.
Система будет иметь отрицательный вещественный корень, если Кр > 0.
Правильный ответ: Кр > 0.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 121.
Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл., стр. 145
!True
Кр > 0
!False
Кр > 1
!False
Kр > 5
!False
Кр > 0,25
!Task 25
Для управления объектом, описываемым апериодическим звеном первого прядка, используется интегральный регулятор, как показано на рисунке

Переходной процесс замкнутой системы будет сходящимся и носить апериодический характер при настройке регулятора …
!Solution
Устойчивость линейной системы определяется по характеру свободного движения. Если свободное движение стремится к нулю при t→ , то такая система является асимптотически устойчивой. Для этого необходимо и достаточно, все корни характеристического уравнения замкнутой системы имели отрицательные вещественные части.
Переходной процесс в устойчивой системе сходится к установившемуся решению. Он носит апериодический характер, если корни характеристического уравнения отрицательные вещественные. Таким образом, по условию задачи необходимо найти значения Кр , при которых корни характеристического уравнения отрицательные вещественные.
Передаточная функция замкнутой системы с отрицательной обратной связью равна

Характеристическое уравнение замкнутой системы имеет вид
λ2 + 4s + 10Кр = 0.
Корнb уравнения определяются по формуле
λ1,2 = - 2 ±√(4 - 10Кр).
Система будет иметь отрицательные вещественные корни, если
0 < Кр < 0,4.
Правильный ответ: 0 < Кр < 0,4.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 121.
Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл., стр. 145
!True
0 < Кр < 0,4
!False
Кр > 1
!False
Kр > 4
!False
Кр > 0,4
!END
*********************************************
*ОТУ 1.3.02.t2.rtf
*********************************************
!Taskfile ОТУ 1.3.02.#Алгебраический критерий устойчивости Гурвица
!DE=ОТУ 1.3.#Устойчивость непрерывных систем управления
!Type=2
!Time=2
Экспертные и технологические параметры заданий:
1. Дисциплина: Основы теории управления
2. Объем часов: группа I (от 80 до 170 часов)
3. Дидактическая единица ГОС: Устойчивость непрерывных систем управления
4. Тема задания: Алгебраический критерий устойчивости Гурвица
5. Уровень сложности: 2 (знать и уметь использовать в типовой учебной ситуации)
6. Ориентировочное время выполнения: 2 минуты
7. Перечень контролируемых учебных элементов
Студент должен знать: алгебраические методы исследования устойчивости систем управления
уметь: по коэффициентам характеристического полинома системы восстанавливать матрицу Гурвица и определять условия устойчивости
8. Форма заданий: выбор одного ответа из четырех предложенных
!Task 1
Матрица Гурвица М для системы:
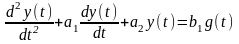
равна …
!Solution
Для исследования устойчивости системы n-го порядка с характеристическим полиномом
D(p) = a0pn + a1pn-1 + ... + an-1p + an
по критерию Гурвица необходимо, используя коэффициенты полинома, построить квадратную матрицу (таблицу) Гурвица размера (n x n) вида

Критерий устойчивости Гурвица сводится к тому, что при а0 > 0 все главные определители матрицы Гурвица должны быть положительными (необходимое и достаточное условие устойчивости).
В данном случае характеристический полином системы равен
D(p) = p2 + a1p + a2 .
Матрица Гурвица рассматриваемой системы имеет вид

Правильный
ответ:

Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 123.
Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл.
!True
!False

!False

!False

!Task 2
Для устойчивости системы с характеристическим полиномом
D(p) = T1T2p3 + (T1+T2)p2 + p + K
при положительных значениях параметров T1 , T2 и К, необходимо и достаточно выполнение условия …
!Solution
Для исследования устойчивости системы n-го порядка с характеристическим полиномом
D(p) = a0pn + a1pn-1 + ... + an-1p + an
по критерию Гурвица необходимо, используя коэффициенты полинома, построить квадратную матрицу (таблицу) Гурвица размера (n x n) вида
Критерий устойчивости Гурвица сводится к тому, что при а0 > 0 все главные определители матрицы Гурвица должны быть положительными (необходимое и достаточное условие устойчивости).
Матрица Гурвица рассматриваемой системы имеет вид

Условие устойчивости системы, при положительных значениях параметров T1 , T2 и К, сводится к выполнению трех неравенств:
Г1 = T1 + T2 > 0 ,
Г2 = T1 + T2 - K T1 T2 > 0,
Г3 = К Г2 > 0.
В свою очередь, приведенные 3 неравенства сводятся к одному:
Г2 = T1 + T2 - K T1 T2 > 0
Правильный ответ: T1 + T2 - K T1 T2 > 0
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 124.
Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл.
!True
T1 + T2 - K T1 T2 > 0
!False
T1 + T2 - T1 T2 > 0
!False
K T1 T2 - T1 - T2 > 0
!False
К - T1 T2 > 0
!Task 3
Для устойчивости системы с характеристическим полиномом
D(p) = a0p3 + a1p2 + a2p + a3
при положительных значениях параметров a0 - a3, необходимо и достаточно выполнение условия …
!Solution
Для исследования устойчивости системы n-го порядка с характеристическим полиномом
D(p) = a0pn + a1pn-1 + ... + an-1p + an
по критерию Гурвица необходимо, используя коэффициенты полинома, построить квадратную матрицу (таблицу) Гурвица размера (n x n) вида
Критерий устойчивости Гурвица сводится к тому, что при а0 > 0 все главные определители матрицы Гурвица должны быть положительными (необходимое и достаточное условие устойчивости).
Матрица Гурвица рассматриваемой системы имеет вид

Условие устойчивости системы, при положительных значениях параметров a0 - a3 , сводится к выполнению неравенств:
Г1 = a1 > 0 ,
Г2 = a1 a2 - a0 a3 > 0,
Г3 = a3 (a1 a2 - a0 a3 ) > 0.
В свою очередь, приведенные 3 неравенства сводятся к одному:
Г2 = a1 a2 - a0 a3 > 0
Правильный ответ: a1 a2 - a0 a3 > 0
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 124.
Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл.
!True
a1 a2 - a0 a3 > 0
!False
a0 a3 - a1 a2 > 0
!False
a0 a3 > 0
!False
a0 + a1 + a2 + a3 > 0
!Task 4
Для системы с характеристическим полиномом
D(p) = p3 + 4p2 + 3p + 2
матрица Гурвица равна …
!Solution
Для исследования устойчивости системы n-го порядка с характеристическим полиномом
D(p) = a0pn + a1pn-1 + ... + an-1p + an
по критерию Гурвица необходимо, используя коэффициенты полинома, построить квадратную матрицу (таблицу) Гурвица размера (n x n) вида
Критерий устойчивости Гурвица сводится к тому, что при а0 > 0 все главные определители матрицы Гурвица должны быть положительными (необходимое и достаточное условие устойчивости).
Матрица Гурвица рассматриваемой системы имеет вид

Правильный
ответ:

Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 118.
Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл.
!True
!False

!False

!False

!Task 5
Для системы 4 порядка с характеристическим полиномом
D(p) = 11р4 + 3p3 + p2 + 5p + 1
матрица Гурвица равна …
!Solution
Для исследования устойчивости системы n-го порядка с характеристическим полиномом
D(p) = a0pn + a1pn-1 + ... + an-1p + an
по критерию Гурвица необходимо, используя коэффициенты полинома, построить квадратную матрицу (таблицу) Гурвица размера (n x n) вида
Критерий устойчивости Гурвица сводится к тому, что при а0 > 0 все главные определители матрицы Гурвица должны быть положительными (необходимое и достаточное условие устойчивости).
Матрица Гурвица рассматриваемой системы имеет вид

Правильный
ответ:

Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 118.
Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл.
!True
!False

!False

!False
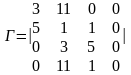
!Task 6
Для системы с характеристическим полиномом
D(p) = p2 + 5p + 2
матрица Гурвица равна …
!Solution
Для исследования устойчивости системы n-го порядка с характеристическим полиномом
D(p) = a0pn + a1pn-1 + ... + an-1p + an
по критерию Гурвица необходимо, используя коэффициенты полинома, построить квадратную матрицу (таблицу) Гурвица размера (n x n) вида
Критерий устойчивости Гурвица сводится к тому, что при а0 > 0 все главные определители матрицы Гурвица должны быть положительными (необходимое и достаточное условие устойчивости).
Матрица Гурвица рассматриваемой системы имеет вид

Правильный
ответ:

Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 118.
Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл.
!True
!False

!False

!False

!Task 7
Автоматическая система будет устойчивой, если все главные определители матрицы Гурвица положительные, а коэффициент при старшей производной в дифференциальном уравнении системы …
!Solution
Для исследования устойчивости системы n-го порядка с характеристическим полиномом
D(p) = a0pn + a1pn-1 + ... + an-1p + an
по критерию Гурвица необходимо, используя коэффициенты полинома, построить квадратную матрицу (таблицу) Гурвица размера (n x n) вида
Критерий устойчивости Гурвица сводится к тому, что при а0 > 0 все главные определители матрицы Гурвица должны быть положительными (необходимое и достаточное условие устойчивости).
Т.е. при положительности всех определителей коэффициент при старшей производной должен быть положительный.
Правильный ответ: положительный.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 118.
Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл.
!True
положительный
!False
отрицательный
!False
любой
!False
любой, ограниченный
!Task 8
Система, порядок уравнения движения которой больше двух, n-ный определитель Гурвица меньше нуля, а все остальные определители и коэффициент при старшей производной характеристического уравнения системы больше нуля, будет …
!Solution
Для исследования устойчивости системы n-го порядка с характеристическим полиномом
D(p) = a0pn + a1pn-1 + ... + an-1p + an
по критерию Гурвица необходимо, используя коэффициенты полинома, построить квадратную матрицу (таблицу) Гурвица размера (n x n) вида
Критерий устойчивости Гурвица сводится к тому, что при а0 > 0 все главные определители матрицы Гурвица должны быть положительными (необходимое и достаточное условие устойчивости).
Т.е., когда n-ный определитель Гурвица меньше нуля, а все остальные определители и коэффициент при старшей производной характеристического уравнения системы больше нуля, система будет неустойчива.
Правильный ответ: неустойчива.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 118.
Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл.
!True
неустойчива
!False
устойчива
!False
находиться на апериодической границе устойчивости
!False
находиться на колебательной границе устойчивости
!Task 9
Система n-ного порядка, n-тый определитель Гурвица которой равен нулю, а все остальные определители и коэффициент при старшей производной характеристического уравнения системы больше нуля, будет …
!Solution
Для исследования устойчивости системы n-го порядка с характеристическим полиномом
D(p) = a0pn + a1pn-1 + ... + an-1p + an
по критерию Гурвица необходимо, используя коэффициенты полинома, построить квадратную матрицу (таблицу) Гурвица размера (n x n) вида
Критерий устойчивости Гурвица сводится к тому, что при а0 > 0 все главные определители матрицы Гурвица должны быть положительными (необходимое и достаточное условие устойчивости).
Т.е., когда n-ный определитель Гурвица равен нулю, а все остальные определители и коэффициент при старшей производной характеристического уравнения системы больше нуля, система будет находиться на границе устойчивости.
Правильный ответ: на границе устойчивости.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 118.
Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл.
!True
на границе устойчивости
!False
устойчива
!False
неустойчива
!False
неопределенной
!Task 10
Матрица Гурвица М для системы:

равна …
!Solution
Для исследования устойчивости системы n-го порядка с характеристическим полиномом
D(p) = a0pn + a1pn-1 + ... + an-1p + an
по критерию Гурвица необходимо, используя коэффициенты полинома, построить квадратную матрицу (таблицу) Гурвица размера (n x n) вида
Критерий устойчивости Гурвица сводится к тому, что при а0 > 0 все главные определители матрицы Гурвица должны быть положительными (необходимое и достаточное условие устойчивости).
В данном случае характеристический полином системы равен
D(p) = p3 + a1p2 + a2р + a3 .
Матрица Гурвица рассматриваемой системы имеет вид

Правильный
ответ:
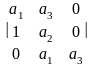
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 118.
Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл.
!True
!False

!False

!False
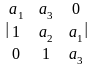
!Task 11
Согласно критерию Гурвица, системы управления 1 или 2 порядков, при положительности коэффициента при старшей производной уравнения движения, будут устойчивы при …
!Solution
Для исследования устойчивости системы n-го порядка с характеристическим полиномом
D(p) = a0pn + a1pn-1 + ... + an-1p + an
по критерию Гурвица необходимо, используя коэффициенты полинома, построить квадратную матрицу (таблицу) Гурвица размера (n x n) вида
Критерий устойчивости Гурвица сводится к тому, что при а0 > 0 все главные определители матрицы Гурвица должны быть положительными (необходимое и достаточное условие устойчивости).
Для систем управления 1 и 2 порядков этот критерий приводит к условию положительности всех коэффициентов характеристического уравнения.
Правильный ответ: положительности всех коэффициентов характеристического уравнения.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 118.
Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл.
!True
положительности коэффициентов характеристического уравнения
!False
отрицательности коэффициентов характеристического уравнения
!False
не отрицательности коэффициентов характеристического уравнения
!False
любых ограниченных значениях коэффициентов характеристического уравнения
!Task 12
Системы первого или второго порядков, у которых все коэффициенты характеристического уравнения имеют одинаковые знаки, будут
!Solution
Для исследования устойчивости системы n-го порядка с характеристическим полиномом
D(p) = a0pn + a1pn-1 + ... + an-1p + an
по критерию Гурвица необходимо, используя коэффициенты полинома, построить квадратную матрицу (таблицу) Гурвица размера (n x n) вида
Критерий устойчивости Гурвица сводится к тому, что при а0 > 0 все главные определители матрицы Гурвица должны быть положительными (необходимое и достаточное условие устойчивости).
Для систем управления 1 и 2 порядков этот критерий приводит к условию положительности всех коэффициентов характеристического уравнения. С другой стороны, если все коэффициенты характеристического уравнения отрицательные, то замена знака на противоположный у всех членов характеристического уравнения сводит данный случай к предыдущему. Поэтому можно утверждать, что если все коэффициенты характеристического уравнения имеют одинаковые знаки, то системы 1 или 2 порядка будут устойчивы.
Правильный ответ: устойчивы.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 118.
Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл.
!True
устойчивы
!False
неустойчивы
!False
на границе устойчивости
!False
неопределены
!Task 13
Условие устойчивости, состоящее в требовании положительности коэффициентов характеристического уравнения, является необходимым и достаточным для систем
!Solution
Для исследования устойчивости системы n-го порядка с характеристическим полиномом
D(p) = a0pn + a1pn-1 + ... + an-1p + an
по критерию Гурвица необходимо, используя коэффициенты полинома, построить квадратную матрицу (таблицу) Гурвица размера (n x n) вида
Критерий устойчивости Гурвица сводится к тому, что при а0 > 0 все главные определители матрицы Гурвица должны быть положительными (необходимое и достаточное условие устойчивости).
Для систем управления 1 и 2 порядков этот критерий приводит к необходимому и достаточному условию положительности всех коэффициентов характеристического уравнения. Поэтому можно утверждать, что если все коэффициенты характеристического уравнения имеют одинаковые знаки, то системы 1 или 2 порядка будут устойчивы.
Правильный ответ: 1 и 2 порядков.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 118.
Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл.
!True
1 и 2 порядков
!False
1 порядка
!False
до 3 порядка включительно
!False
любого порядка
!Task 14
Движение системы описывается дифференциальным уравнением
где: y(t) - выходная переменная, g(t) - задающее воздействие, t - время.
Автоматическая система
!Solution
Для исследования устойчивости системы n-го порядка с характеристическим полиномом
D(p) = a0pn + a1pn-1 + ... + an-1p + an
по критерию Гурвица необходимо, используя коэффициенты полинома, построить квадратную матрицу (таблицу) Гурвица размера (n x n) вида
Критерий устойчивости Гурвица сводится к тому, что при а0 > 0 все главные определители матрицы Гурвица должны быть положительными (необходимое и достаточное условие устойчивости).
Для систем управления 1 и 2 порядков этот критерий приводит к необходимому и достаточному условию положительности всех коэффициентов характеристического уравнения. Поэтому можно утверждать, что если все коэффициенты характеристического уравнения имеют одинаковые знаки, то системы 1 или 2 порядка будут устойчивы.
В данном случае характеристический полином системы равен
D(p) = p2 + 1 .
Так как один из коэффициентов полинома равен нулю, то можно утверждать, что система на границе устойчивости.
Правильный ответ: на границе устойчивости.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 118.
Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл.
!True
на границе устойчивости
!False
устойчива
!False
неустойчива
!False
может быть устойчивой или неустойчивой в зависимости от вида задающего воздействия
!Task 15
Движение системы описывается дифференциальным уравнением
где: y(t) - выходная переменная, g(t) - задающее воздействие, t - время.
Автоматическая система будет находиться на границе устойчивости при …
!Solution
Для исследования устойчивости системы n-го порядка с характеристическим полиномом
D(p) = a0pn + a1pn-1 + ... + an-1p + an
по критерию Гурвица необходимо, используя коэффициенты полинома, построить квадратную матрицу (таблицу) Гурвица размера (n x n) вида
Критерий устойчивости Гурвица сводится к тому, что при а0 > 0 все главные определители матрицы Гурвица должны быть положительными (необходимое и достаточное условие устойчивости).
Для систем управления 1 и 2 порядков этот критерий приводит к необходимому и достаточному условию положительности всех коэффициентов характеристического уравнения. Поэтому можно утверждать, что если все коэффициенты характеристического уравнения имеют одинаковые знаки, то системы 1 или 2 порядка будут устойчивы.
В данном случае характеристический полином системы равен
D(p) = p2 + А .
Если А < 0, то согласно критерию система неустойчива. При А > 0, из-за равенства нулю коэффициента полинома а1, можно утверждать, что система на границе устойчивости. Следовательно, система будет находиться на границе устойчивости при А > 0.
Правильный ответ: А > 0.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 118.
Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл.
!True
А > 0
!False
А < 0
!False
А ≠0
!False
любом А
!Task 16
Движение системы описывается дифференциальным уравнением
где: y(t) - выходная переменная, g(t) - задающее воздействие, t - время.
Автоматическая система …
!Solution
Для исследования устойчивости системы n-го порядка с характеристическим полиномом
D(p) = a0pn + a1pn-1 + ... + an-1p + an
по критерию Гурвица необходимо, используя коэффициенты полинома, построить квадратную матрицу (таблицу) Гурвица размера (n x n) вида
Критерий устойчивости Гурвица сводится к тому, что при а0 > 0 все главные определители матрицы Гурвица должны быть положительными (необходимое и достаточное условие устойчивости).
Для систем управления 1 и 2 порядков этот критерий приводит к необходимому и достаточному условию положительности всех коэффициентов характеристического уравнения. Поэтому можно утверждать, что если все коэффициенты характеристического уравнения имеют одинаковые знаки, то системы 1 или 2 порядка будут устойчивы.
В данном случае характеристический полином системы равен
D(p) = p2 + 3р .
Так как равен нулю коэффициент полинома а2, можно утверждать, что система на границе устойчивости.
Правильный ответ: на границе устойчивости.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 118.
Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл.
!True
на границе устойчивости
!False
устойчива
!False
неустойчива
!False
может быть устойчивой или неустойчивой в зависимости от вида задающего воздействия
!Task 17
Передаточная функция замкнутой системы имеет вид
Замкнутая система …
!Solution
Для исследования устойчивости системы n-го порядка с характеристическим полиномом
D(p) = a0pn + a1pn-1 + ... + an-1p + an
по критерию Гурвица необходимо, используя коэффициенты полинома, построить квадратную матрицу (таблицу) Гурвица размера (n x n) вида
Критерий устойчивости Гурвица сводится к тому, что при а0 > 0 все главные определители матрицы Гурвица должны быть положительными (необходимое и достаточное условие устойчивости).
Для систем управления 1 и 2 порядков этот критерий приводит к необходимому и достаточному условию положительности всех коэффициентов характеристического уравнения. Поэтому можно утверждать, что если все коэффициенты характеристического уравнения имеют одинаковые знаки, то системы 1 или 2 порядка будут устойчивы.
В данном случае характеристический полином системы равен
D(p) = p2 + 4р + 3 .
Так как все коэффициенты полинома положительные, то можно утверждать, что система устойчива.
Правильный ответ: устойчива.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 118.
Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл.
!True
устойчива
!False
неустойчива
!False
на границе устойчивости
!False
может быть устойчивой или неустойчивой в зависимости от вида задающего воздействия
!Task 18
Передаточная функция разомкнутой системы имеет вид
При замыкании отрицательной обратной связью система будет …
!Solution
Для исследования устойчивости системы n-го порядка с характеристическим полиномом
D(p) = a0pn + a1pn-1 + ... + an-1p + an
по критерию Гурвица необходимо, используя коэффициенты полинома, построить квадратную матрицу (таблицу) Гурвица размера (n x n) вида
Критерий устойчивости Гурвица сводится к тому, что при а0 > 0 все главные определители матрицы Гурвица должны быть положительными (необходимое и достаточное условие устойчивости).
Для систем управления 1 и 2 порядков этот критерий приводит к необходимому и достаточному условию положительности всех коэффициентов характеристического уравнения. Поэтому можно утверждать, что если все коэффициенты характеристического уравнения имеют одинаковые знаки, то системы 1 или 2 порядка будут устойчивы.
В данном случае передаточная функция замкнутой системы с отрицательной обратной связью равна
Характеристический полином системы имеет вид
D(p) = p2 + 10 .
Так как равен нулю коэффициент полинома а1, можно утверждать, что система на границе устойчивости.
Правильный ответ: на границе устойчивости.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 118.
Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл.
!True
на границе устойчивости
!False
устойчива
!False
неустойчива
!False
может быть устойчивой или неустойчивой в зависимости от вида задающего воздействия
!Task 19
Передаточная функция разомкнутой системы имеет вид
Замкнутая отрицательной обратной связью система будет устойчивой при значениях коэффициента передачи К …
!Solution
Для исследования устойчивости системы n-го порядка с характеристическим полиномом
D(p) = a0pn + a1pn-1 + ... + an-1p + an
по критерию Гурвица необходимо, используя коэффициенты полинома, построить квадратную матрицу (таблицу) Гурвица размера (n x n) вида
Критерий устойчивости Гурвица сводится к тому, что при а0 > 0 все главные определители матрицы Гурвица должны быть положительными (необходимое и достаточное условие устойчивости).
Для систем управления 1 и 2 порядков этот критерий приводит к необходимому и достаточному условию положительности всех коэффициентов характеристического уравнения. Поэтому можно утверждать, что если все коэффициенты характеристического уравнения имеют одинаковые знаки, то системы 1 или 2 порядка будут устойчивы.
Передаточная функция замкнутой системы с отрицательной обратной связью равна
Характеристический полином системы имеет вид
D(p) = p + К-1 .
Для положительности коэффициентов полинома требуется выполнения неравенства К > 1.
Правильный ответ: > 1.
Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 118.
Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл.
!True
> 1
!False
< 1
!False
> 0
!False
< -1
!Task 20
