
3.2.2. Общая постановка задачи изменения условий выплаты платежей
При решении задачи изменения условий выплаты платежей составляется уравнение консолидации по следующему правилу: «Старые» долги равны «новым» долгам, но и те, и другие должны быть приведены на одну дату консолидации. Дата консолидации либо устанавливается во взаимном соглашении, либо выбирается произвольно.
Пример 7. Две суммы 12 и 8 млн. руб. должны быть выплачены 1.09.00 (244) и 1.01.01 (1). Стороны договорились пересмотреть условия контракта: должник 1.12.00 (335) выплачивает 10 млн. руб., остаток долга гасится 1.04.01 (91). Найти эту сумму при условии, что пересчет осуществляется по ставке простых процентов, равной 12% (год равен 365 дней).
Решение.
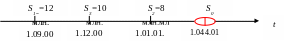
Возьмем за базовую дату 1.04.01 и составим уравнение эквивалентности, учитывая два условия:
1) все платежи приведены к базовой дате;
2) старые долги равны новым долгам.
Т.к.
базовая дата самая поздняя из всех, то
платежи
![]() и
и
![]() наращиваются.
наращиваются.
![]()
![]()
![]() млн.
руб.
млн.
руб.
Пример 8. Заменить следующий поток платежей: 200 тыс. руб. через один год, 175 тыс. руб. – через два года, 210 тыс. руб. – через 4 года, эквивалентным множеством, состоящим из двух выплат, равных по величине: первая – через 1.5 года, вторая – через 3 года. Проценты начисляются по ставке 8% годовых каждые 6 месяцев.
Решение.
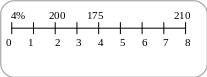
Эффективная
ставка за полгода равна 4%. Составим
уравнение эквивалентности для настоящего
момента времени. Оно имеет следующий
вид:
![]() .
Отсюда
найдем величину выплат
P:
.
Отсюда
найдем величину выплат
P:
![]() тыс.
руб.
тыс.
руб.
Пример 9. Согласно контракту необходимо уплатить 100 тыс. руб. через 5 лет. Стороны договорились изменить условия погашения долга следующим образом: через 2 года выплачивается 30 тыс. руб., а оставшийся долг – спустя четыре года после первой выплаты. Найти суму последнего платежа, если i=10%.
Решение.
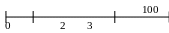


4
6
Уравнение эквивалентности можно составить на любой момент времени. Запишем его, например, для начального момента времени:
![]() ;
;
![]() тыс.
руб.,
тыс.
руб.,
где
![]() .
.
Для другой даты, например конец шестого года, уравнение примет вид:
30(1+i)4+P=100(1+i),
откуда
P=100(1+i)-30(1+i)4=133,233 тыс. руб.
