1º. Самолетные углы

При описании движений самолетов используется следующая связанная система координат (см. рис. 3.5.1).

Ось — продольная ось симметрии самолета; положительное направление от хвостовой части к кабине самолета.

Ось — в продольной плоскости симметрии, направлена от шасси вверх по вертикали.

Ось — в направлении правого крыла перпендикулярно продольной плоскости симметрии.

Рис. 3.5.1

Для задания ориентации самолета применяется следующая схема ввода углов ориентации:

— угол курса, , — угол тангажа, , — угол крена, .

Здесь имеем особенность при .

Матрица ориентации имеет вид:

.

2º. Корабельные углы

При описании движений кораблей используется следующая связанная система координат (см. рис.3.5.2).

Рис. 3.5.2

Ось — по оси симметрии от кормы к носовой части.

Ось — ортогональна продольной плоскости симметрии, направлена от правого борта на левый борт.

Ось — в продольной плоскости симметрии от днища корабля вверх к палубе.

Схема ввода углов ориентации:

— дифферент корабля, ,

— крен корабля, ,

— угол рысканья корабля, .

Матрица ориентации имеет вид:

.

Здесь имеем особенность при .

§6. Алгебраический метод построения матрицы ориентации

Определение

Будем называть матрицей элементарного поворота матрицу перехода от системы координат, построенной поворотом исходной системы координат вокруг одной из ее координатных осей на один угол.

Очевидно, существует три независимых элементарных поворота.

1. Поворот вокруг 1-ой оси (оси ) на угол  (см. рис. 3.6.3).

Рис. 3.6.3

Тогда

.

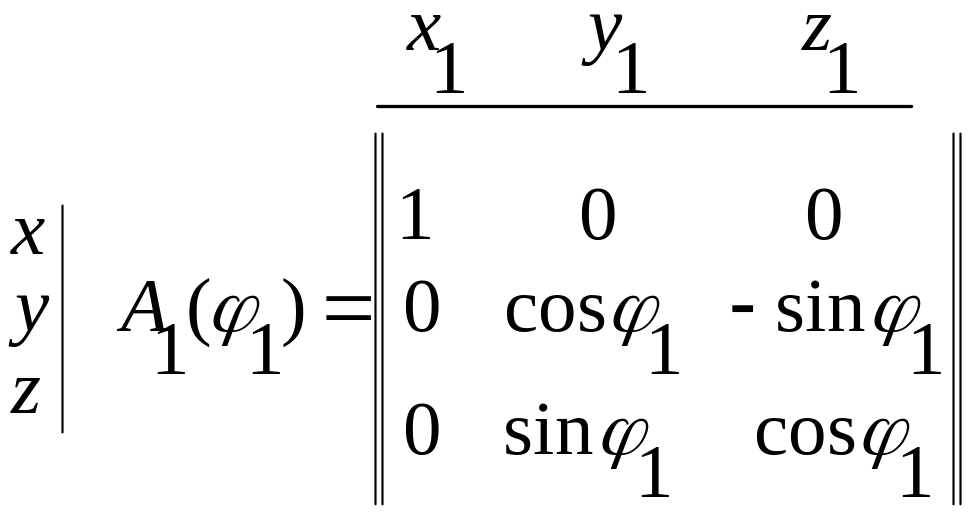2. Поворот вокруг 2-ой оси (оси ) на угол 

,

Рис. 3.6.4

Тогда

.

3. Поворот вокруг 3-ой оси (оси ) на угол  (см. рис. 3.6.5).

Рис. 3.6.5

Тогда

.

Если обозначить исходную систему координат через , а систему, полученную элементарным поворотом с номером на угол  , через , то можем записать

, .

Теперь обратимся к схеме ввода углов ориентации.

Как отмечено в п.2  §4, эти углы вводятся тремя последовательными поворотами вокруг одной из осей согласно схеме, задающей последовательность поворотов и углов, на которые осуществляется поворот.

Например, для углов Эйлера имеем:

После первого поворота можем записать

.

После второго и третьего поворотов соответственно получим

, .

Подставляя зависимость от в предшествующую формулу, а затем полученную зависимость в формулу связи с , получим

.

Поскольку ,

где и — координаты любой (произвольной) точки соответственно в системе и , то отсюда находим

.

Аналогично для самолетных и корабельных углов будем иметь:

— для самолетных углов,

— для корабельных углов.

Этот способ вычисления матрицы ориентации может применяться к любой схеме ввода углов ориентации.