3º. Физический смысл углов Эйлера
Поясним физический смысл углов Эйлера. Рассмотрим их на примере движения волчка.
Наблюдения показывают, если пренебречь трением опоры волчка, то ось симметрии волчка совершает следующее движение.
Обозначим
— конец орта оси симметрии, начало
системы координат —
,
а
— проекцию точки
на плоскость
.
Точка находится в плоскости во все время движения, причем, если конструктивно волчок выполнен точно (т.е. является симметричным относительно оси вращения, и все его массы расположены симметрично), то точка движется по окружности.
Радиус
окружности равен
,
где
— угол между осями
и
(см. рис. 3.4.5).
Об этом движении говорят, что волчок совершает прецессию.
Точнее говоря, прецессией волчка называют вращение вокруг вертикальной оси плоскости, проходящей через эту ось и ось симметрии волчка.
Если
симметрия волчка конструктивно нарушена,
то точка
одновременно с прецессией, т.е. вращением
вокруг полюса
в плоскости
,
совершает колебательное движение между
двумя окружностями радиуса
и
(см. рис. 3.4.6).
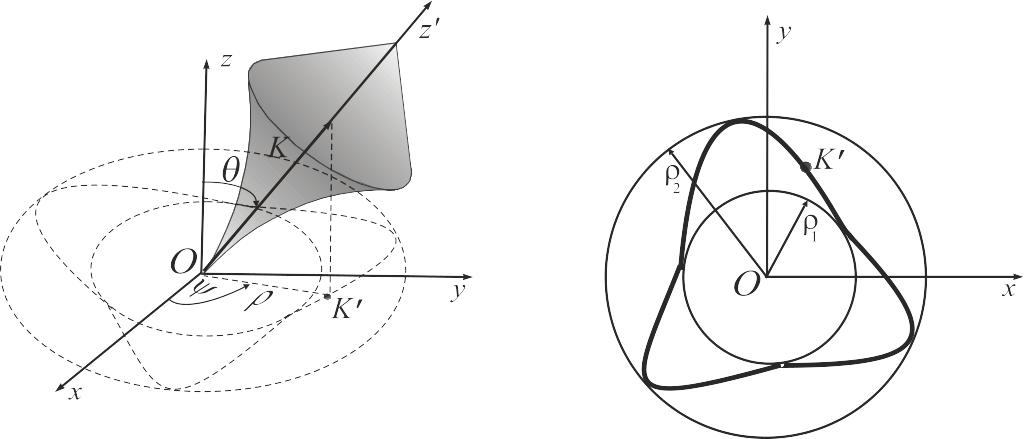
Рис. 3.4.5 Рис.3.4.6
Здесь
— минимальное значение угла
,
а
— максимальное. Иначе говоря,
— колебательная функция. Такое движение
волчка называется его нутационным
колебанием.
Все остальные материальные точки волчка, расположенные вне оси симметрии, по отношению к этой оси совершают круговые движения по углу . Их движения называется собственным вращением волчка.
Таков физический смысл углов Эйлера. Отсюда они получили название:
– угол
прецессии,
;
– угол
нутации,
;
– угол собственного вращения, .
4º. Построение углов Эйлера по заданной матрице ориентации
Дадим ответ на следующий вопрос:
если матрица задана, то можно ли определить углы Эйлера по ее элементам?
Матрица имеет вид:
.
Из третьего столбца матрицы находим
,
,
.
Из третьей строки матрицы получим
,
.
Эти
соотношения справедливы только в том
случае, когда
,
т.е. при
и
.
При
и
матрица
,
соответственно, принимает вид:
;
.
Из
данных выражений матрицы
можно вычислить по первому столбцу при
только угол
и угол
при
.
Эта особенность принципиальная, ибо при и при плоскости и совпадают, и понятие линии узлов отсутствует.
В такой ситуации в качестве линии узлов можно взять любую прямую, находящуюся в плоскости .
И если по общему правилу задать углы и относительно линии узлов, то по этим углам однозначно будут вычисляться элементы матрицы , поскольку положение осей по отношению к при определяется суммой углов , а при — разностью углов .
Однако обратная задача — задача определения значений углов Эйлера по элементам матрицы — не будет иметь решения, поскольку углы и не могут быть вычислены при и .
§5. Выражение матриц ориентации твердого тела через самолетные и корабельные углы