Решение.

В таблице каждому значению Х соответствует статистическое распределение признака У.

Х = 15

У	32	42	52	62	72
nху	1	-	-	-	-

Отсюда находим среднее значение У при условии, что Х = 15, или условную среднюю:

_Х=15 = = 32

Х = 20

У	32	42	52	62	72
nху	5	3	-	-	-

_Х=20 = = 35,75

Х = 25

У	32	42	52	62	72
nху	-	5	9	4	-

_Х=25 = 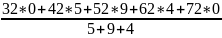= 51,44;

Х = 30

У	32	42	52	62	72
nху	-	-	40	11	4

_Х=30 = 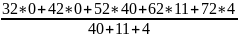= 55,45;

Х = 35

У	32	42	52	62	72
nху	-	-	2	6	7

_Х=35 = 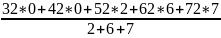= 65,33;

Х = 40

У	32	42	52	62	72
nху	-	-	-	-	3

_Х=40 = 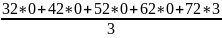= 72.

Каждому значению У соответствует статистическое распределение Х.

У = 32

Х	15	20	25	30	35	40
nху	1	5	-	-	-	-

Отсюда находим условную среднюю:

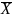_У=32 = 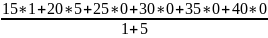= 19,2;

У = 42

Х	15	20	25	30	35	40
nху	-	3	5	-	-	-

_У=42 = = 23,13;

У = 52

Х	15	20	25	30	35	40
nху	-	-	9	40	2	-

_У=52 = 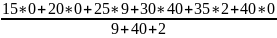=29,31;

У = 62

Х	15	20	25	30	35	40
nху	-	-	4	11	6	-

_У=62 = 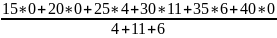=30,47;

У = 72

Х	15	20	25	30	35	40
nху	-	-	-	4	7	3

_У=72 = = 34,64.

Оценка тесноты линейной связи между признаками Х и У производится с помощью коэффициента линейной корреляции r:

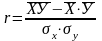
Х	nx	X  nx	X2  nx	Ух	Х  nх  Ух
15	1	225	225	32	480
20	8	3200	3200	35,75	5720
25	18	11250	11250	51,44	23148
30	55	49500	49500	55,45	91492,5
35	15	18375	18375	65,33	34298,25
40	3	4800	4800	72	8640
	100	2920	87350	-	163778

У	nу	У  nу	У2  nу	Ху	У  nу  Ху
32	6	192 6144	6144	19,2	3686,4
42	8	336	14112	23,13	7771,68
52	51	2652	137904	29,31	77730,12
62	21	1302	80724	30,47	39671,94
72	14	1008	72576	34,64	34917,12
	100	5490	311460	-	163778

Контроль:  Х  n_х  У_х =  У  n_у  Х_у = 163778.

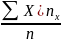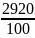= = = 29,2;

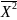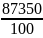= = = 873,5;

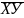= = = 1637,78;

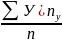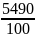= = = 54,9;

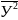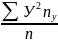= = =3114,6;

σ_х = 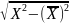= 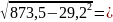4,57;

σ_У = = 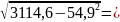10,03;

находим коэффициент корреляции:

r = = 0,76;

Так как r > 0, то связь прямая, то есть с ростом Х растёт У.

Так как r = 0,76, то по таблице определяем, что линейная связь высока.

Находим линейное уравнение регрессии У на Х:

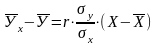
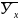- 54,9 = 0,76 * 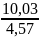(Х – 29,2);

- 54,9 =1,67*(Х – 29,2);

= 1,67Х + 6,14;

Находим линейное уравнение регрессии Х на У:

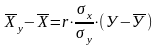
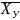- 29,2 = 0,76 * (У – 54,9);

- 29,2 = 0,35 * (У – 54,9);

= 0,35У + 9,99

Данные уравнения устанавливают связь между признаками Х и У и позволяют найти среднее значение признака 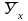для каждого значения Х и аналогично среднее значение признака для каждого значения У.

Изобразим полученные результаты графически.

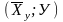Нанесем на график точки , отметив их (*). Нанесем на график точки отметив их (). Построим каждое из найденных уравнений регрессии по двум точкам:

= 1,67Х + 6,14;

Х	5	20
У	14,49	39,54

= 0,35У + 9,99

Х	15	30
У	14,31	57,17

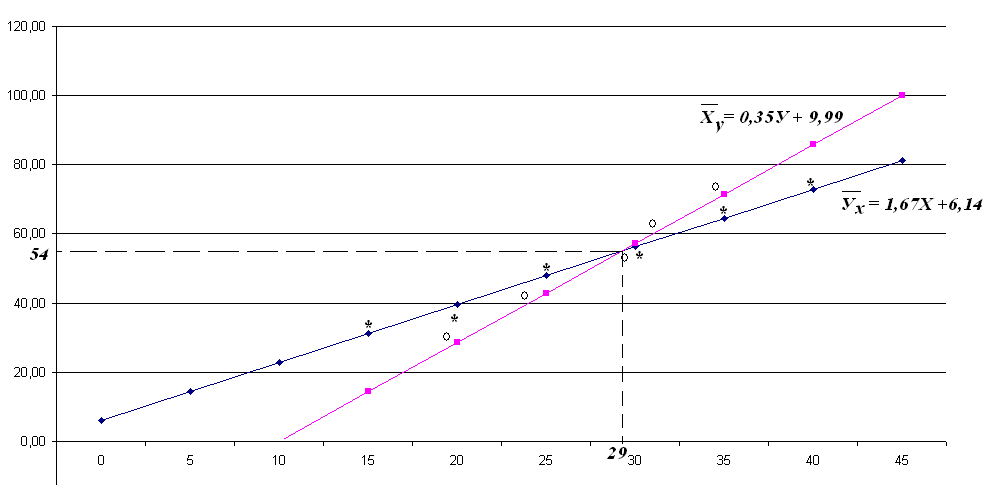
Прямые регрессии пересекаются в точке (29; 54).

Оценка тесноты любой связи между признаками производится с помощью корреляционных отношений У к Х и Х к У:

;

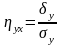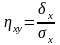
Найдены ранее σ_х = 4,57; σ_У = 10,03.

Найдём 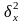и

= =

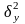
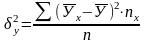
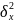= ≈ 13,44;

= +

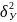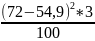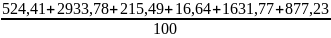+ = ≈ 61,99;

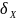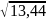= ≈3,67;

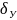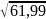= ≈ 7,87;

корреляционные отношения равны:

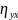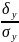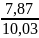= = ≈ 0,78;

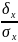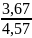= = ≈ 0,8;

Ответ: Корреляционная связь между признаками высокая, ее можно описать линейными уравнениями:

= 1,67Х + 6,14; = 0,35У + 9,99.

0 < 0,76 < 0,78< 1; 0 < 0,76 < 0,8 < 1.

10