Задание 1Технолог вызывает мастера по внутрисистемной рации. Вероятность того, что мастер примет первый вызов равна 0,2, второй – 0,4 и третий – 0,8. Условия приёма таковы, что событие, состоящее в том, что i-ый по счету вызов услышан, независимы, i= 1, 2, 3. Найти вероятность того, что мастер вообще услышит технолога.

Решение.

Введем в рассмотрение события, вероятности которых заданы:

А₁– мастер примет первый вызов, Р(А₁) =0,2, Р(Ā₁) = 1 – 0,2 = 0,8;

А₂ – мастер примет второй вызов, Р(А₂) = 0,4, Р(Ā₂) = 0,6;

А₃ – мастер примет третий вызов, Р(А₃) = 0,8, Р(Ā₃) = 0,2;

С – вероятность того, что мастер вообще услышит технолога;

В₀ – ни один из вызовов не будет услышан.

Р(В₀) = Р(Ā₁Ā₂Ā₃) = 0,8 * 0,6 * 0,2 = 0,096;

С = 1 - 0,096 = 0,904.

Ответ: вероятность того, что мастер вообще услышит технолога, равна 0,904.

Задание 2 Контролер ОТК проверяет однотипный вид продукции, поступающий из трех цехов, производительности которых относятся как 1:2:3. Брак составляет в среднем: для первого цеха – 2%, для второго – 1,5%, для третьего – 2,5%. Взятая наудачу деталь оказалась бракованной. Какова вероятность того, что она поступила из третьего цеха.

Решение.

Пусть событие А – деталь бракованная. Возможны три гипотезы. Рассмотрим каждую и вычислим её вероятность.

Н₁ – деталь изготовлена в первом цехе. Р(Н₁) = ;

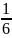Н₂ – деталь изготовлена во втором цехе. Р(Н₁) = = ;

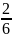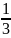Н₃ – деталь изготовлена в третьем цехе. Р(Н₁) = .

Рассмотрим условные вероятности события А:

Р_Н1 = 0,02;

Р_Н2 = 0,015;

Р_Н3 = 0,025;

Полная вероятность события А равна:

Р(А) = * 0,02 + * 0,015 + * 0, 025 = = = .

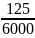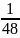Вычислим вероятность того, что бракованная деталь поступила из третьего цеха:

Р_А(Н₃) = 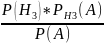= = 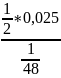0,6.

Ответ: вероятность того, что бракованная деталь поступила из третьего цеха, равна 0,6.

Задание 3.Гормолзавод снабжает молочной продукцией n магазинов. Вероятность того, что в течении дня поступит заявка на товар, равна р для каждого магазина. Найти вероятность того, что в течении дня: а) поступит к заявок; б) не менее к₁ и не более к₂ заявок; в) поступит хотя бы одна заявка. Каково наивероятнейшее число поступающих в течении дня заявок и чему равна соответствующая ему вероятность?

27. р = 0,7; n = 21; k = 12; k₁ = 10; k₂ = 15;

Решение.

а) вероятность того, что в течении дня поступит 12 заявок:

Р_n(k) = С_n^k · р^k· q ^n-k = 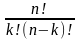· р^k· q ^n-k, где q = 1 – р;

q = 1 – 0,7 = 0,3;

Р_n(12) = 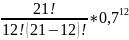* 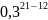= 293930*0,7¹²*0,3⁹ =0,080077718 ≈ 0,08;

вероятность того, что в течении дня поступит 12 заявок равна 0,08.

б) Вероятность того, что в n испытаниях событие наступит не менее k раз и не более m раз, находится по формуле:

Р_n(k) + Р_n(k+1) + Р_n(k+2) + … + Р_n(m)

Р_n(10) + Р_n(11) + Р_n(12) + Р_n(13) + Р_n(14) + Р_n(15);

Р_n(10) = 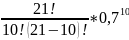* 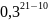= 0,017649783 ≈ 0,02;

Р_n(11) = 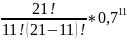* = 0,041182826 ≈ 0,04;

Р_n(12) = * = 0,080077718 ≈ 0,08;

Р_n(13) = 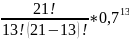* = 0,129356313 ≈ 0,13;

Р_n(14) = 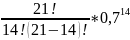* 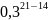= 0,172475084 ≈ 0,17;

Р_n(15) = 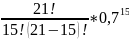* = 0,187806203 ≈ 0,19;

0,02 + 0,04 + 0,08 + 0,13 + 0,17 + 0,19 = 0,63.

Вероятность того, что в течении дня поступит не менее 10 и не более 15 заявок равна 0,63.

в) поступит хотя бы одна заявка, k = 1.

Найдём вероятность противоположного события, ни одна заявка не поступит.

Р_n(0) = 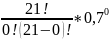* 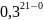= 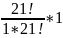* = 0,00000000001046035320

≈ 0,00000000001;

Р = 1 - 0,00000000001 = 0,9999999999.

Вероятность того, что в течении дня поступит хотя бы одна заявка равна 0,9999999999.

Наивероятнейшее число поступающих в течении дня заявок и соответствующая ему вероятность.

n*p – q 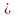k₀ n*p + p;

21*0,7 – 0,3 ≤ k₀≤ 21*0,7 + 0,3;

14,4 ≤ k₀≤ 15.

Наивероятнейшее число поступающих в течении дня заявок 15.

Р_n(15) = * = 0,187806203 ≈ 0,19.

Ответ:

а) Вероятность того, что в течении дня поступит 12 заявок равна 0,08.

б) Вероятность того, что в течении дня поступит не менее 10 и не более 15 заявок равна 0,63.

в) Вероятность того, что в течении дня поступит хотя бы одна заявка равна 0,9999999999.

Наивероятнейшее число поступающих в течении дня заявок 15; Р_n(15) = 0,19.

Задание 4.

37. Случайная величина Х задана функцией распределения F(x). Найти плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины, если: .

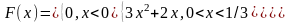Решение.

F(x) =

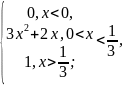
Плотность распределения f(x):

f(x) = F’(x) =

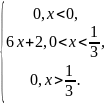
Математическое ожидание:

М(Х) = .

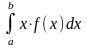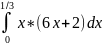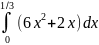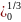M(X) = = = (6* x³ + 2* x² ) = 2*( )³ +( )² =

= 2*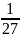 + 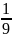= + 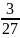= 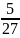≈ 0,185.

Дисперсия случайной величины:

D(X) = 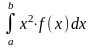- (M(X))².

D(X) = 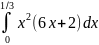- (M(X))² = - (M(X))² =

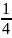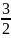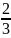= (6 * x⁴ + 2 * x³) - (M(X))² = ( )⁴ + ( )³ - (M(X))² =

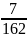= * + * – 0,185² = - 0,185² = 0,04321 – 0,034225 = 0,008985.

Ответ:

плотность распределения вероятностей f(x) = F’(x) =

Математическое ожидание M(X) = 0,185.

Дисперсия случайной величины D(X) = 0,008985.

Задание 5.

Заданы математическое ожидание «а» и среднее квадратическое отклонение «σ» нормально распределенной случайной величины Х. Требуется найти: а) вероятность того, что Х примет значение, принадлежащее интервалу (α, β), б) вероятность того, что абсолютная величина отклонения «Х - а» окажется меньше δ.

47. а = 9, σ = 5, α = 5, β = 15, δ = 8.

Решение.

а) Найдем вероятность того, что Х примет значение, принадлежащее интервалу (5, 15) по формуле:

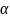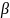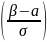Р( <х< ) = Ф - Ф ,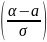

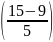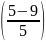Р(5<х<15) = Ф - Ф = Ф - Ф = Ф(1,2) – Ф(-0,8) =

= Ф(1,2) + Ф(0,8) = 0,3849 + 0,2881 = 0,673.

Искомая величина попадания нормально распределенной случайной величины в интервал (5; 15) равна: Р(5<х<15) = 0,673.

б) Вероятность того, что абсолютная величина отклонения «Х - а» окажется меньше δ.

Р(|х - a|<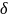 ) = 2*Ф( / ),

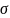Р(|x – 9|< 8) = 2*Ф(8/5) = 2*Ф(1,6) = 2*0,4452 = 0,8904.

Ответ: а) Вероятность того, что Х примет значение, принадлежащее интервалу (5, 15) равна Р(5<х<15) = 0,673.

б) Вероятность того, что абсолютная величина отклонения «Х - а» окажется меньше δ, равна Р(|x – 9|< 8) = 0,8904.