2.7. Математична теорія теплового вибуху

Перебіг екзотермічної хімічної реакції в будь яку ізольовану (замкнуту) систему повинно привести до вибуху.

Адіабатичний тепловий вибух

Розглянемо граничний випадок - адіабатичну (теплоізольовану) систему, в якій протікає екзотермічна хімічна реакція. Швидкість реакції описується кінетичним рівнянням

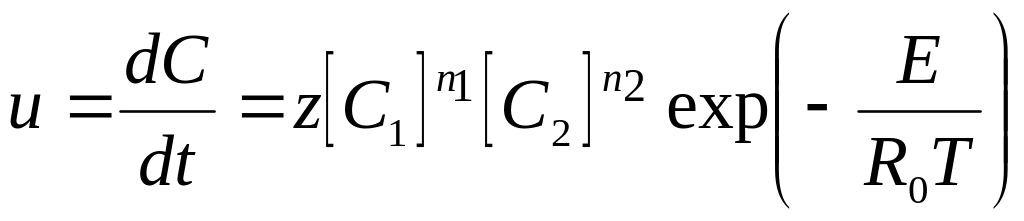
де С, С₁, С₂ - концентрації продуктів реакції і реагентів;

z, E - предекспонент і енергія активації;

Т - абсолютна температура;

R₀ - універсальна газова постійна;

n₁, n₂ - Порядок реакції по першому і другому реагентів.

Нехай q - тепловий ефект реакції на один моль продукту С, що утворюється в ході реакції. Оскільки система теплоізольована і займає постійний обсяг, то швидкість зміни температури Т в системі визначається рівнянням

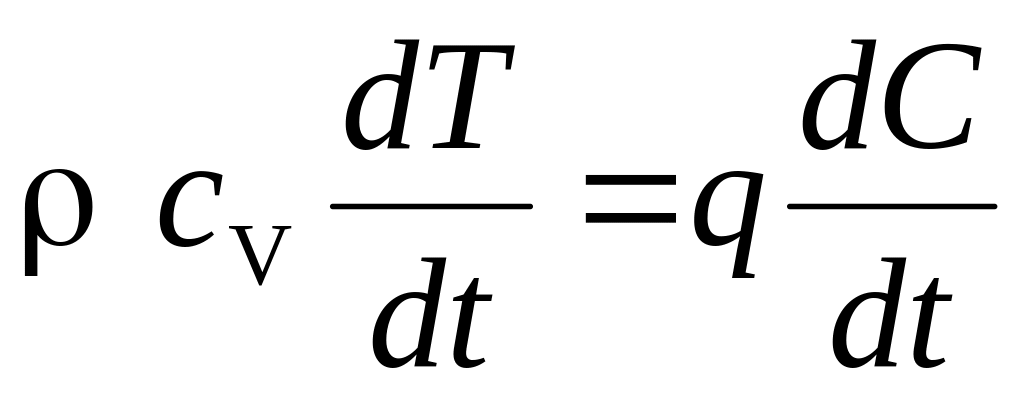
де - питома теплоємність при постійному обсязі;

ρ - щільність суміші.

Припустимо, що q >> с_V T₀ (початкової енергії системи).

Тоді протікання екзотермічної реакції в ізольованій системі буде приводити до істотного підвищення температури навіть при малому вигорянні вихідних компонентів суміші. Рівняння (2.2) з урахуванням (2.1) можна представити у вигляді

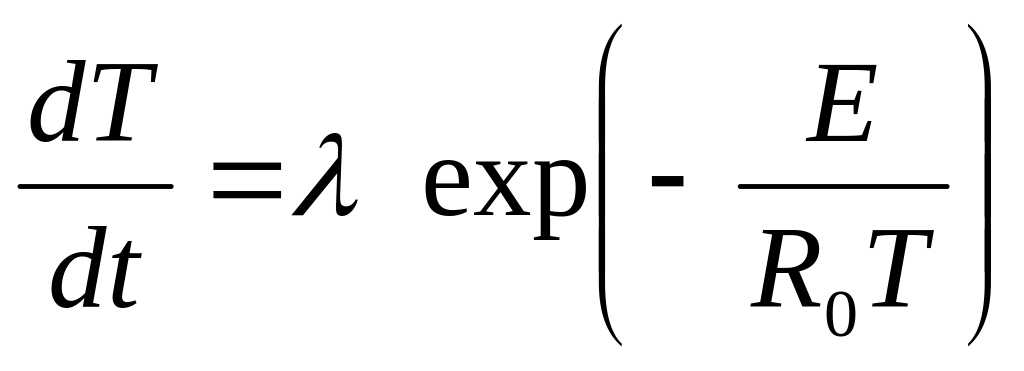
де

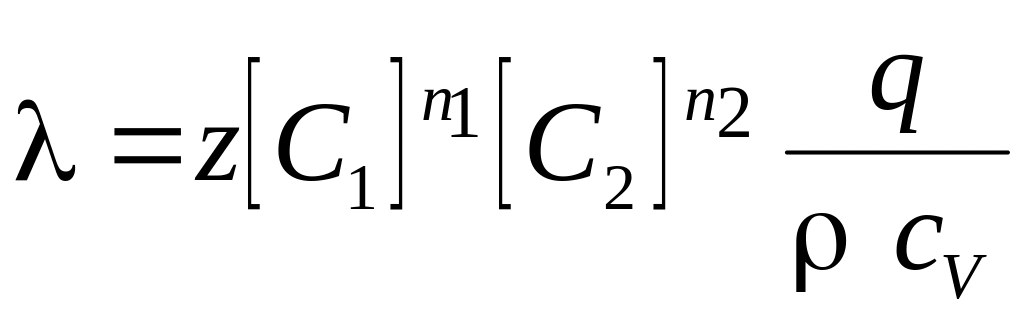
Інтегруючи рівняння (2.3) з урахуванням початкової умови Т (t = 0) = T₀, одержимо

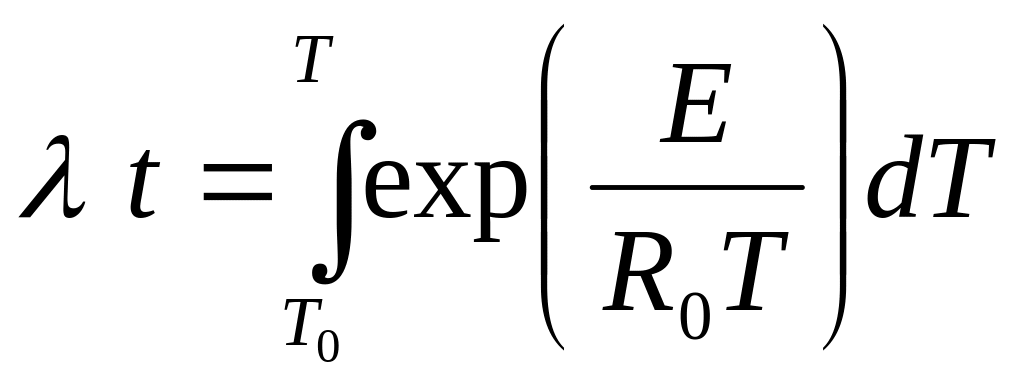
Або

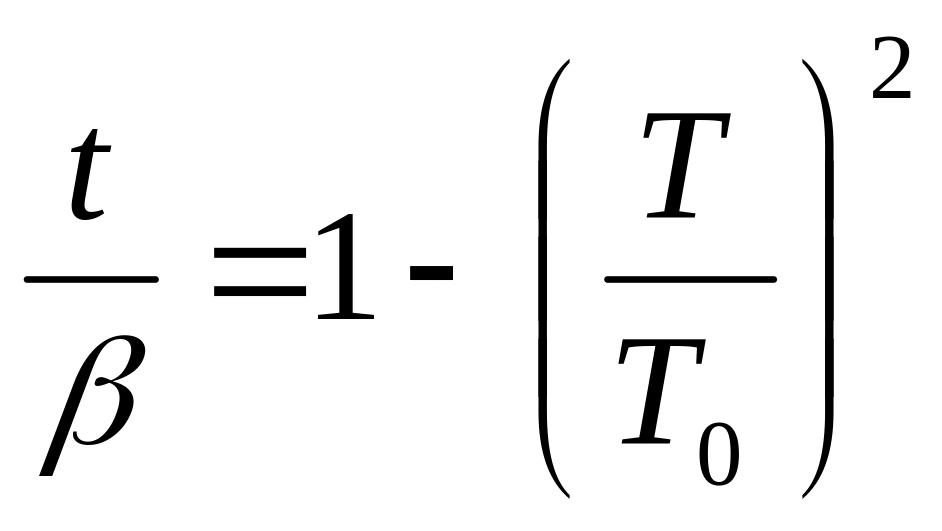
Де

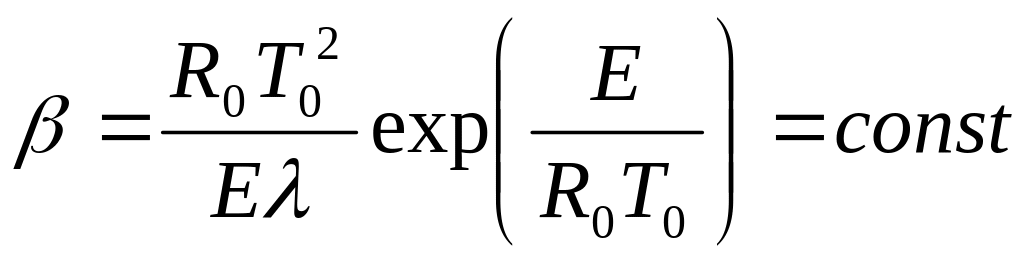
Результати розрахунків за рівнянням (2.4), наведені на рис. 2.7, показують, що зі зростанням часу t температура Т плавно зростає до моменту часу t/β = 1, а потім зростання температури різко прискорюється. Це явище називається тепловим вибухом. Проміжок часу t_в =  називається періодом індукції (часом затримки запалення) теплового вибуху в теплоізольованій системі з екзотермічною реакцією:

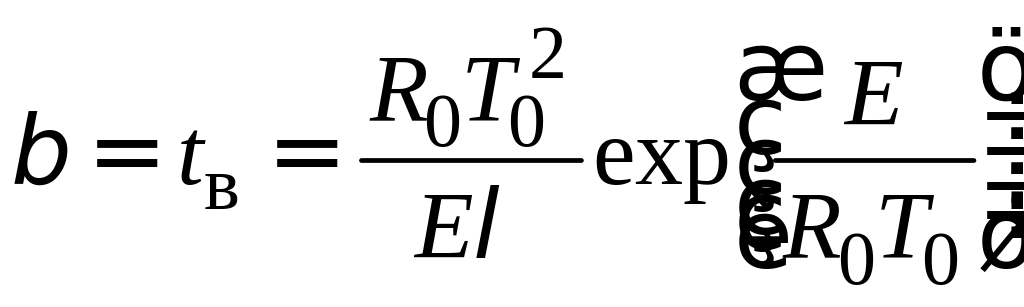
Рис. 2.7. Залежність температури адіабатичної системи від часу для різних значень параметра Е/(R₀T₀)

З графіків, наведених на рис. 2.7, випливає, що зі збільшенням початкової температури Т₀ час затримки запалення (період індукції) t_в знижується.

Тепловий вибух в неадіабатичних умовах

У реальних системах завжди відбуваються втрати теплоти за рахунок теплопровідності через стінки, конвекції, випромінювання і т.д. При цьому екзотермічна реакція буде або прискорюватися, призводячи до вибуху, або протікати з постійною швидкістю при постійній температурі T=const, яка визначається тепловим балансом системи. Так, зокрема, протікають екзотермічні реакції горіння в газових печах, котельних топках та інших теплотехнічних агрегатах. При наявності теплових втрат рівняння (2.2) набуде вигляду

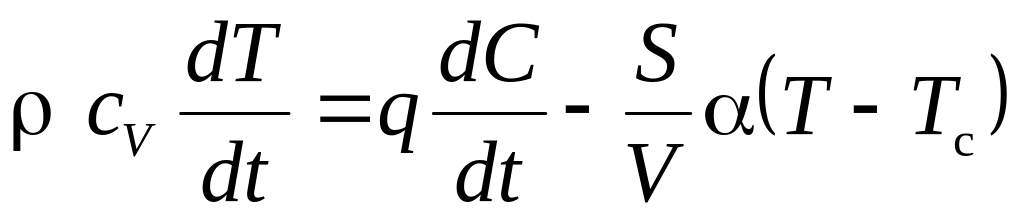
де V - об'єм реактора;

S - площа поверхні стінок реактора;

T_с - температура стінок реактора;

α - коефіцієнт теплопередачі.

Перша складова різниці в правій частині рівняння (2.5) описує швидкість виділення тепла в системі за рахунок хімічної реакції. Друга складова - швидкість відводу тепла за рахунок теплопровідності стінок, яка лінійно залежить від температури реагуючої суміші. Швидкість припливу тепла зростає по статичному закону із зростанням початкової концентрації компонентів , і експоненціально зростає із зростанням температури T відповідно до закону Арреніуса.

Позначимо через графіки залежності швидкості тепловиділення Q + і швидкості тепловтрат Q-від температури Т, які наведені на рис. 2.8 для трьох значень D:

D₁ > D_кр > D_2.

З аналізу наведених графіків, які представляють собою діаграму Семенова, випливає, що при D = D1, криві Q +, Q-не мають точок перетину; при D = D_кр, криві Q+, Q-мають одну точку дотику; при D = D2, криві Q +, Q-мають дві точки перетину. У першому випадку (D = D1) швидкість тепловиділення завжди перевищує швидкість тепловтрат, і в системі обов'язково відбудеться тепловий вибух, так як температура суміші буде необмежено зростати. Другий випадок (D = D_кр), коли має місце торкання кривих тепловиділення і тепловтрат, визначає максимальне значення концентрації реагентів (параметра D), при якому швидкість тепловиділення дорівнює швидкості тепловтрат.

Рис. 2.8. Вплив температури неадіабатичної системи на швидкість тепловиділення та швидкість тепловтрат

Всі інші криві Q + для більш низьких значень концентрації реагентів перетинають криву Q-двічі. Причому, стійкому стану системи відповідає лише нижня точка з більш низькою температурою Т_уст.

Таким чином, якщо концентрація реагентів не перевищує певного критичного для даної системи значення, то температура суміші в реакторі буде постійною T = Т_уст т = const, причому Т_уст > Тс.

При виконанні цієї умови після деякого перехідного періоду в хімічному реакторі встановлюється стаціонарний режим, при якому швидкість екзотермічної реакції буде мати постійне значення u = const. На рис. 2.9 наведено три режими роботи реактора у вигляді залежності температури від часу T = f(t).

Рис. 2.9. Режими роботи реактора

Температура Т2 відповідає максимальній температурі в реакторі, при якій можливо стійке протікання хімічної реакції (при заданих значеннях С₁, С₂, Т_с). Можна показати,що величина Т₂ визначається формулою

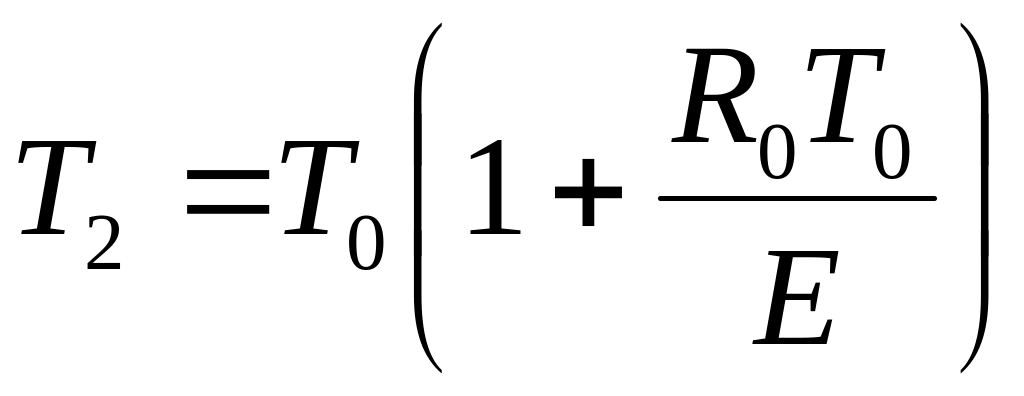
Температура Т₂ пов'язана з параметрами реактора наступним співвідношенням:

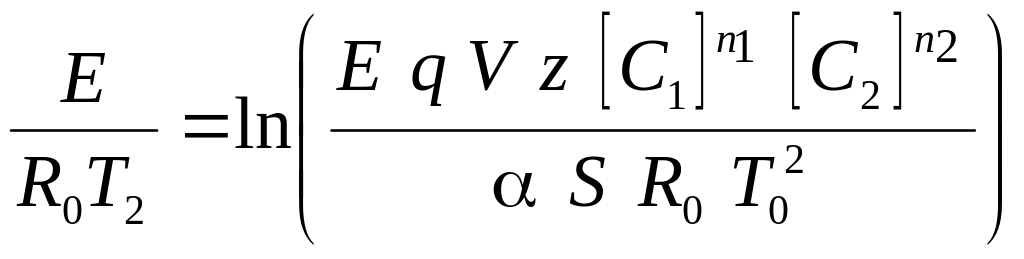
Це рівняння дозволяє визначити вибухобезпечність кожного конкретного реактора. Позначимо

Z₁ = ,

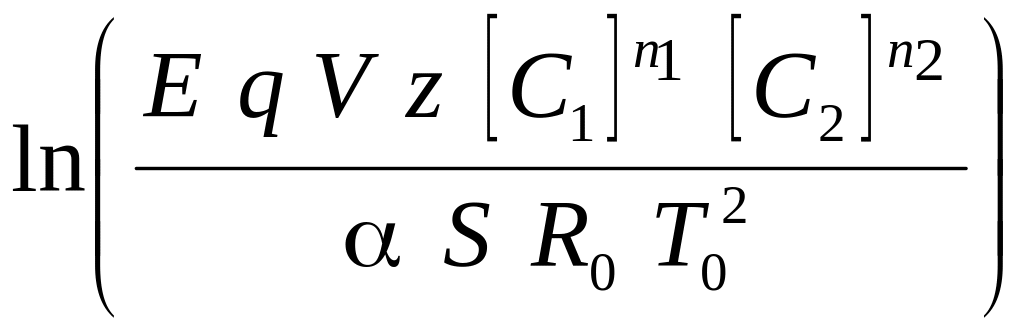
Якщо Z₂  Z₁, то реактор вибухобезпечний, якщо Z₂  Z₁, то ситуація є критичною,тобто можна очікувати вибуху; при Z₂  Z₁ в реакторі обов'язково відбудеться тепловий вибух. Для розрахунку тиску в реакторі по відомій швидкості зростання температури dT/dt використовується рівняння стану (рівняння Менделєєва-Клапейрона)

де p, , T, R - тиск, щільність, абсолютна температура і газова постійна продуктів згоряння в реакторі. Газова постійна продуктів згоряння R розраховується за формулою

R = c_p – c_v,

де cp, cv - питомі теплоємності продуктів згоряння при постійному тиску і постійному об’ємі, відповідно.