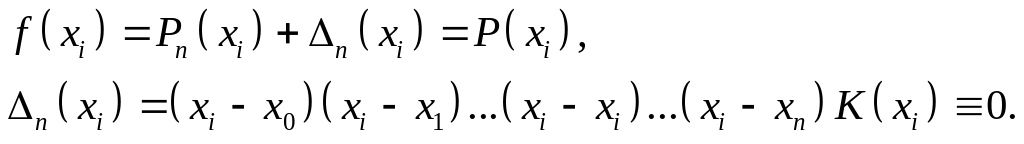10

1. Погрешность интерполяции

При приближении функции полиномом степени n выбираются узловые точки и находится многочлен , проходящий через эти точки. Поскольку этот многочлен предполагается использовать вместо первоначальной функции , важно рассмотреть вопрос о том, как сильно могут отличаться функция и многочлен в точках, отличных от узловых (где они совпадают в пределах ошибки округления) . Представим функцию в виде , где - остаточный член в форме Лагранжа (погрешность интерполяции).

- интерполяционный многочлен степени n. Получим выражение для остаточного члена в предположении, что:

1. , т. е. функция имеет на отрезке непрерывные производные вплоть до порядка включительно.

2. и при

Теоретическое выражение для разности между первоначальной функцией и интерполяционным многочленом может быть найдено, если заметить, что разность равна нулю во всех узловых точках. Поэтому будем искать остаточный член в следующем виде:

где - полином порядка (заведомо известно, что погрешность равна нулю во всех узлах интерполяции); - некоторая функция, значение которой в узлах можно задать произвольно, т. к.

Если значение x не совпадает с узлами, то

Зафиксируем произвольное значение _, для любого i и рассмотрим вспомогательную функцию :

В соответствии с исходными данными функция имеет непрерывную производную, то же справедливо и для функции . Очевидно, , при и при т. е. обращается в нуль в точках.

Для дальнейшего определения значения воспользуемся теоремой Ролля.

Теорема Ролля: Пусть функция определена и непрерывна в замкнутом промежутке ; существует конечная производная , по крайней мере, в открытом промежутке ; на концах промежутка функция принимает равные значения . Тогда между точками и найдется такая точка , что .

Рассмотрим отрезок . Будем последовательно брать в качестве отрезка отрезки , ... и т.д. Функция удовлетворяет всем трем условиям теоремы Ролля на этих отрезках. Следовательно, обращается в нуль по крайней мере в точках отрезка . Между двумя нулями гладкой функции лежит нуль ее производной. Но тогда вторая производная функция равна 0 в точках по той же причине и т.д. Таким образом, найдется хотя бы одна точка , в которой . , где – полином степени и поэтому его производная –го порядка тождественно равна нулю:

- полином степени с коэффициентом при старшей степени 1 и, следовательно,

Поэтому

и

Тогда

где - некоторая неизвестная точка.

Так как производная по предположению непрерывна на (см.условие 1), то она ограничена на этом отрезке, поэтому обозначим:

Оценка погрешности интерполяции в точке х:

(1)

Оценка погрешности интерполяции на всем отрезке :

(2)

Рис.1 Интерполяция функции Рунге полиномом степени n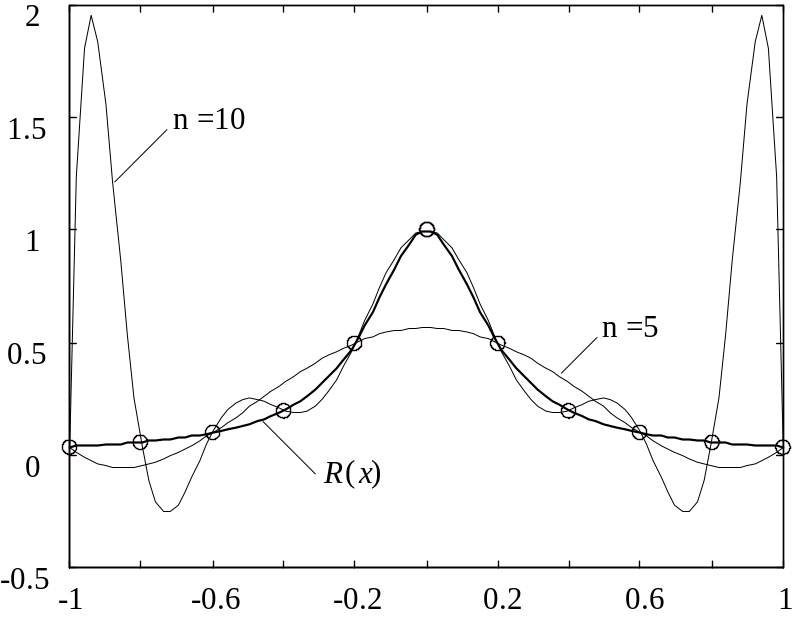

Теперь посмотрим, что получится, если интерполировать известную функцию f(x) все в большем и большем числе точек на фиксированном интервале. Выражение для погрешности (1) состоит из трех разных частей: факториал и произведение разностей с увеличением n уменьшают ошибку, но порядок производной при этом растет. Для многих функций величина M_n+1 увеличивается быстрее, чем (n+1)!. В результате полиномиальные интерполянты редко сходятся к обычной непрерывной функции. Практический эффект выражается в том, что интерполирующий полином высокой степени может вести себя «плохо» в точках, отличных от узлов интерполяции (x_i, y_i), . Поэтому на практике часто используют интерполянты степени не выше 5-6.

Примером может служить функция Рунге [4] вида f(x)=1/(1+25x²), график которой представлен на рис. 1. С увеличением порядка интерполирующего полинома при равномерном распределении узлов интерполяции на интервале [–1, 1] происходит ухудше­ние качества приближения на краях интервала. Это объясняется тем, что производные f(x), которые фигурируют в выражении для погрешности интерполяции (2), быстро растут с увеличением числа n.