§ 19. Косое произведение векторов в v2

Из предыдущего параграфа обратим внимание на необходимое и достаточное условие коллинеарности векторов: | |² | |² - | |² = 0 Û | | .

Пусть на плоскости E² зафиксирована декартова система координат.

Пусть = (x_a, y_a), = (x_b, y_b). Рассмотрим выражение | |² | |² - | |² в координатах:

| |² | |² - | |² = (x_a² + y_a ²) (x_b² + y_b²) – (x_a x_b + y_a y_b)² = (x_a y_b - y_a x_b)²

Итак, два вектора ,  V² коллинеарны, тогда и только тогда, когда x_a y_b - y_a x_b = 0.

Определение. Косым произведением векторов , Î V² в данной системе координат  будем называть число, которое вычисляется по формуле x_a y_b - y_a x_b.

Обозначение: _

Замечание. Естественно возникает вопрос, насколько косое произведение зависит от системы координат.

Определение. Будем говорить, что параллелограмм ABCD натянут на не коллинеарные векторы и , если = и =

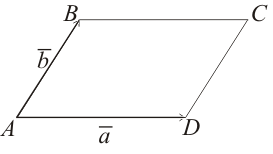
РИС. 30

Теорема.

(1) Ù_w = 0  | | для любых векторов , Î V², в любой декартовой системе координат ;

(2) Если векторы и не коллинеарны, то | Ù_w | = S, где S – площадь параллелограмма, натянутого на векторы и , в любой системе декартовой координат ;

(3) Ù = , где = (x_a, y_a), = (x_b, y_b), для любых векторов , Î V²;

(4) Ù_w = Ù_w’ , если декартовы системы координат  и ’ориентированы одинаково;

Ù_w = - Ù_w’ , если декартовы системы координат  и ’имеют противоположные ориентации.

Доказательство.

Пункт (1) является прямым следствием определения;

(2) По определению косого произведения

| Ù_w |² = | |² | |²- | |² = | |² | |² - | |²| |²cos² = | |² | |²(1 – cos²) = | |² | |²sin² = S² (где  - угол между векторами и );

(3) По определению определителя = x_a y_b - y_a x_b;

(4) Пусть A – матрица перехода от системы координат ’ к системе координат .

Тогда для любого вектора = A , где - координаты вектора в системе , - координаты вектора в системе координат ’.

Ù_w’ = = = det A (x_a y_b - y_a x_b) = det A Ù_w

Если  ~ ’, то det A = 1 и Ù_w = Ù_w’ , иначе det A = -1 и Ù_w = - Ù_w’ .

Замечание.

Свойства (1), (2), (4) из вышеуказанной теоремы показывают, что модуль косого произведения векторов не зависит от выбора декартовой системы координат, а при смене системы координат у косого произведения векторов измениться знак, если новая и старая системы координат ориентированы противоположно.

Следствие.

Для неколлинеарных векторов ,  V² косое произведение положительно в системе координат  тогда, и только тогда, когда базиса системы координат  и пара векторов { , } ориентированы одинаково. (То есть, Ù_w > 0   ~ { , })

Доказательство.

Если векторы и не коллинеарны, то пара { , } образует базис пространства .

Определитель матрицы перехода от фиксированного в декартовой системе координат базиса к базису { , }будет следующим: = = Ù_w .

Так, что по определению одинаковой ориентированности базисов Ù_w > 0 тогда, и только тогда, когда w ~ { , }.

Замечание. В дальнейшем будем опускать знак системы координат в обозначении косого произведения, и считать, что на плоскости зафиксирована декартова система координат.

Теорема. (Алгебраические свойства косого произведения).

(1) Антисимметричность: Ù = - Ù для любых двух векторов , Î V²;

(2) Линейность по первому аргументу:

( + ) Ù = Ù + Ù для любых векторов , ,  V²,

( ) Ù =  Ù для любых векторов , Î V², для любого числа l Î R;

(3) Линейность по второму аргументу:

Ù( + ) = Ù + Ù для любых векторов , , Î V²,

Ù ( ) = l Ù для любых векторов , Î V², для любого числа l Î R.

Доказательство.

Свойства (1) – (2) являются прямым следствием определения.

Пусть векторы , и имеют следующие координаты:

= (x_a, y_a), = (x_b, y_b), = (x_c, y_c).

(1) Ù = x_a y_b - y_a x_b = - (y_a x_b - x_a y_b) = - Ù ;

(2) ( + ) Ù = (x_a + x_b)y_c – (y_a + y_b)x_c = (x_a y_c - y_a x_c) + (x_b y_c - y_b x_c) = Ù + Ù ;

(l ) Ù = (( x_a)y_b - (y_a) x_b) =  (x_a y_b - y_a x_b) = l Ù ;

Свойство (3) следует из свойств (1) и (2).

Упражнения.

1) Вычислите площадь треугольника ABC, используя косое произведение векторов, если в декартовой системе координат A(-3,2), B(1,4), C(2,-1).

2) Какие из свойств косого произведения сохраняться, если его вычислять по той же формуле в аффинной системе координат, которая не является декартовой?

3) Пусть на плоскости задан треугольник ABC. Докажите, что для любой точки O на плоскости S_ABC = |  +  +  |, где = , = , = .

Попробуйте обобщить эту формулу на случай многоугольника.