Добавил:

Hidi Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МЭИ»

Предмет:

Гидрогазодинамика

Файл:

Лекции гидродинамика Тф-14 / ГЛАВА 4. ПОГРАНСЛОЙ.ppt

Скачиваний:

133

Добавлен:

26.05.2014

Размер:

359.42 Кб

Скачать

☆

4. Пограничный слой

4.1. Ламинарный погранслой

При Re ? 1 - ситуация очень малой вязкости, так что жидкость можно

рассматривать как идеальную. Однако, у идеальных жидкостей на твердых стенках - касательная компонента скорости отлична от нуля, а у вязких – равна нулю! Отсюда вывод: скорость до нуля вблизи твердых границ должна падать до нуля в очень тонком слое около тела. Такой слой носит название пограничного. Граница этого слоя не является, естественно, резкой и переход между погранслоем и внешним потоком жидкости непрерывен.

Рассмотрим систему уравнений, которыми описываются течения в тонком погранслое вблизи тела. Пусть имеет место двумерное обтекание жидкостью плоского участка поверхности тела (вдоль оси x). Тогда уравнения Навье-Стокса для стационарного течения имеют вид:

1 p

U(x)

1 p

(4.1)

vx vy 0x y

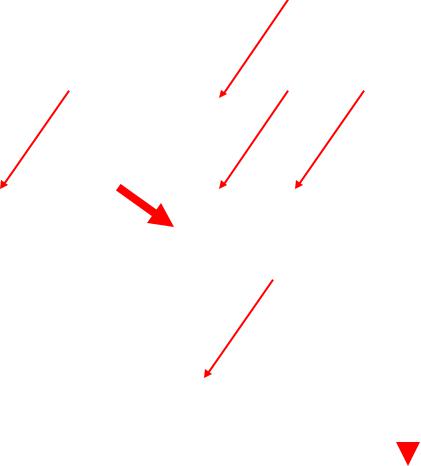
Из уравнения неразрывности следует, что

vx / Lx : vy / Ly vx : vy (Lx / Ly ) vy (L / ) vx ? vy

Из уравнения Навье-Стокса:

vx / x = vx / y; 2vx / x2 = 2vx / y2

Откуда:

В пограничном слое силы вязкости соизмеримы с силами инерции!

1 p

2 v

x x

y y

1 p

vx vx vy vx

x y

p 0y

vx vy 0x y

1 p		2 vx	Здесь учтено,	что	в
	x	y2	пограничном	слое	нет
			поперечного	градиента

давления!

(4.2)	Людвиг
	Людвиг
	Прандтль
- уравнения пограничного слоя Прандтля (1904г.)	1875 — 1953гг.
- уравнения пограничного слоя Прандтля (1904г.)

Уравнения пограничного слоя Прандтля (4.2) – незамкнуты: неизвестны компоненты скорости и давление; Прандтль предложил в первом приближении не учитывать обратного влияния погранслоя на внешний поток; поскольку толщина погранслоя мала, то распределение давления и скорости можно взять из внешнего (вне погранслоя) течения). Поскольку вне погранслоя течение потенциальное, то можно записать уравнение Бернулли:

U(x)	у	Потенциальное	p ( U 2	/ 2) const	1 dp	U	dU
		течение
		течение			dx		dx
					dx		dx
			Окончательно получаем уравнения Прандтля
		x	Окончательно получаем уравнения Прандтля
		x	в форме:

2 v

1 dp

Уравнения

пограничного слоя

(4.3)

Прандтля (1904г.)

Граничные условия имеют вид:

vy 0 при

y 0

(4.4)

U (xпри)

Подобные уравнения можно получить не только при обтекании плоской стенки, но и в более сложных случаях геометрии тел

Если ввести безразмерные переменные:

x Lx' , y Ly' /

Re , vx

U0 v'x , vy U0v'y /

Re;

U U0U ' , Re U0 L /

U0 - скорость на бесконечности; тогда

2 v'

dU '

v'y

v'x

v'y

U '

;

(4.5)

Нетрудно видеть, что в новых переменных уравнения не содержат вязкости! Это означает, что решения этих уравнений не содержат числа Рейнольдса. Таким образом, течение в пограничном слое при изменении числа Рейнольдса изменяется подобна сама себе: продольные расстояния и скорости остаются неизменными, а поперечные меняются обратно пропорционально корню из числа Рейнольдса!

Кроме того, нетрудно показать, что:

v'x : v'y : 1; это означает, что vy : U0 / Re

Отношение поперечной скорости к продольной обратно пропорционально Re !

При этом толщина погранслоя есть
: L / Re	(4.6)

4.2. Ламинарный погранслой на пластине (задача Блазиуса)

В 1908 г. Блазиус рассмотрел задачу о погранслое на плоской полубесконечной

пластине

Пусть скорость основного потока равна:

U const

Тогда из уравнений (4.3) следует:

v vx

(4.7)

В задаче о полубесконечной пластине нет никаких характерных параметров длины; отсюда введем следующие величины:

Re U0 x	;	x /	Re; y /	U0 / x ; y	U0 / x

Вводим функцию тока:

vx ; vy y x

Тогда для безразмерной функции тока имеем:

/ U0 / x ; vx /U0 d / d ' ( )

Или получаем:

U ' ( ); v

/ x (

x ) / x

U / x ' ( / 2x)

''U0

U0 / x

2 v				v			d	v		x
		x				x

y	2		y		y		d
									y

'''		U		/ x	U	'''	2	/ x
U	0	U	0	/ x	U	x U	0	/ x
	0		0		o		0

vx	d (vx /U0 ) / d U0 / x		U0 '' ( / 2x)
x
Откуда:			1						2
	U 'U	( / 2x) ''		U / x( ' )U		U		/ x ''	2
	U 'U	( / 2x) ''		U / x( ' )U	0	U	o	/ x ''	U0	'''
	0 0		2	0	0		o
Тогда:			2						x
Тогда:			2 ''' '' 0							(4.8)
			2 ''' '' 0							(4.8)

Граничные условия для (4.8):					y 0 : vx 0 0 : ' 0;					(4.9)
					y 0 : vy 0 0 : 0;					(4.9)
					y : vx U0 : ' 1;
Решение уравнения (4.8) с граничными условиями можно получить только
численно.						' ( ) 1при ? 1
	' ( )					' ( ) 1при ? 1
	' ( )				Толщина погранслоя
1.0					Толщина погранслоя
1.0						y vx U0
0.8						y vx U0
0.8					За толщину погранслоя принимают следующее
					За толщину погранслоя принимают следующее
					условие
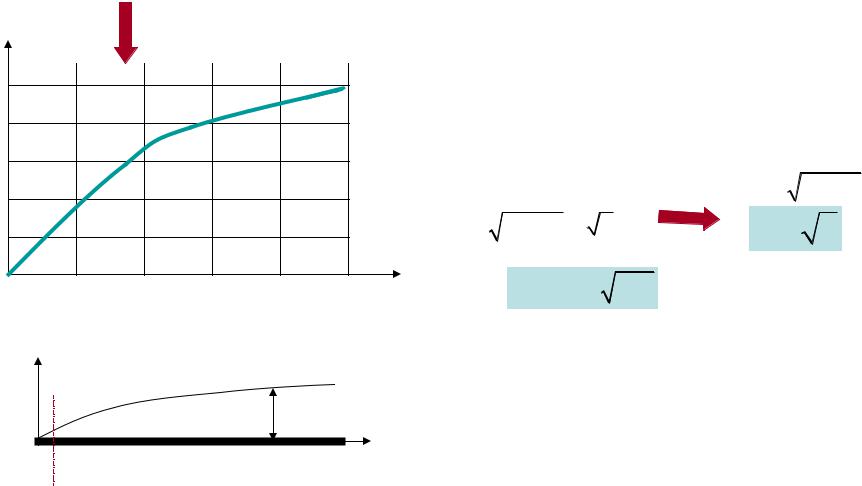
0.4						y ,если v / Uпри0,99 (1%)U			x	/ 5
						x	0			0
						5 x /U0 :		x	:	x
						Или				(4.10)
0	1.0	2.0	3.0	4.0	5.0	/ x 5 /		Rex		(4.10)
						Если Rex : / x 0 (= 1)
	y					Rex 0 : / x (? 1)
						Таким образом,		вблизи	начала	пластины
						решение Блазиуса несправедливо – имеется
						решение Блазиуса несправедливо – имеется

0 x xmin	x	x xmin

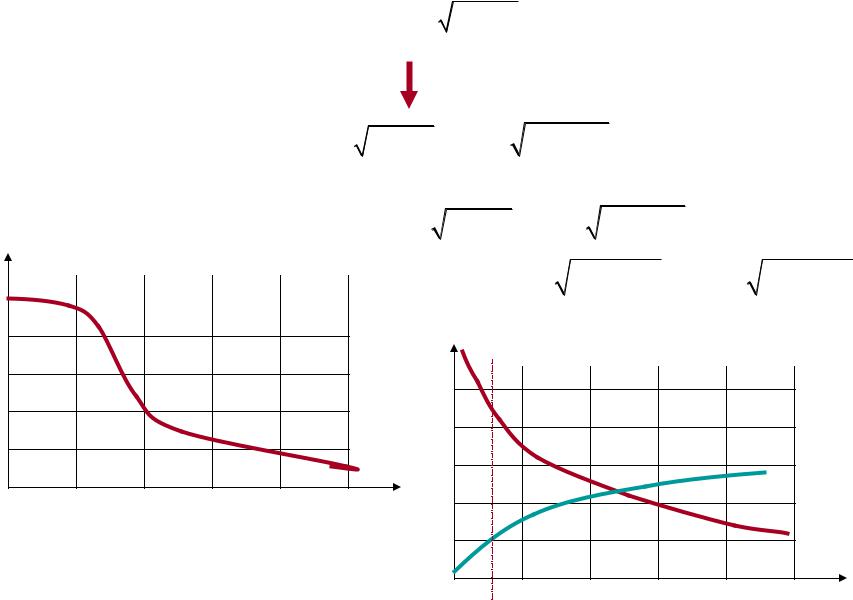
Касательные напряжения и сила трения на пластине

'' ( )U

/ x

xz yz 0

U0 / (U0 / )( / x)2

	xy '' ( )U0	U0 / x '' ( ) U03 / x
Касательные напряжения:
	xy ( 0) '' (0)U0 U0		/ x '' (0) U03 / x
	xy / xy (0)	xy (0)	'' (0) U03 / x 0,332	U03 / x
1.0

xy (0)

1.0

2.0

3.0

4.0

5.0

x xmin

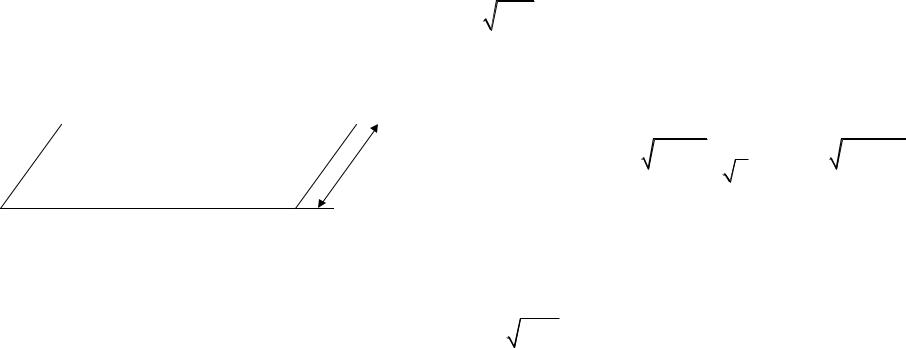
Местный коэффициент сопротивления трения:

cf xy (0) /( U02 / 2) cf

0,664 / Rex ,где Re

U0/x

Сила трения, действующая на всю пластину:

	F	L	2		(0)bdx 0,664b	U 3	L	dx	1,328b	U 3L
b
	ò ð			xy		0		x		0

		0					0

Средний коэффициент сопротивления трения:

c	f	2F	/ S U 2	1,328 /	Re	L
	f	тр	0			L

Пределы применимости решения Блазиуса: xmin x xcr

Оценки:

2 vx / x2 = 2vx / y2	(U0 / x2 ) = (U0 / 2 )пусть	( /	)xmin0, 01	Re(	xmin)2500
Recr	(3 10)g105 = Re(xmin ) = Rex		= (3 10)g105

Соседние файлы в папке Лекции гидродинамика Тф-14