Добавил:

Hidi Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МЭИ»

Предмет:

Гидрогазодинамика

Файл:

Лекции гидродинамика Тф-14 / ГЛАВА 3. ВЯЗКАЯ ЖИДКОСТЬ new.ppt

Скачиваний:

185

Добавлен:

26.05.2014

Размер:

8.24 Mб

Скачать

☆

1 / 31 2 3 > Следующая >>>

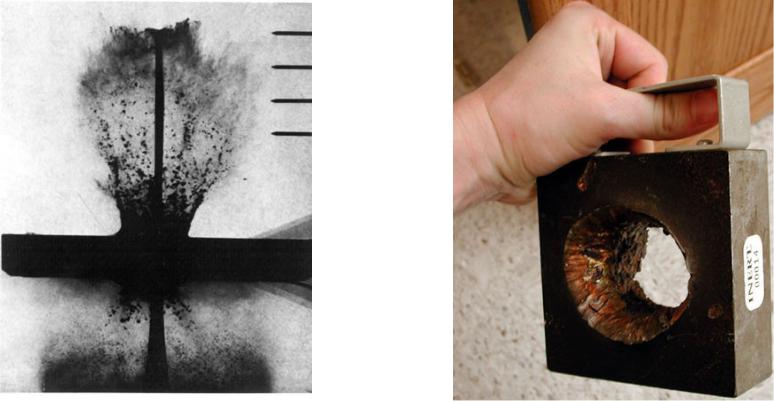
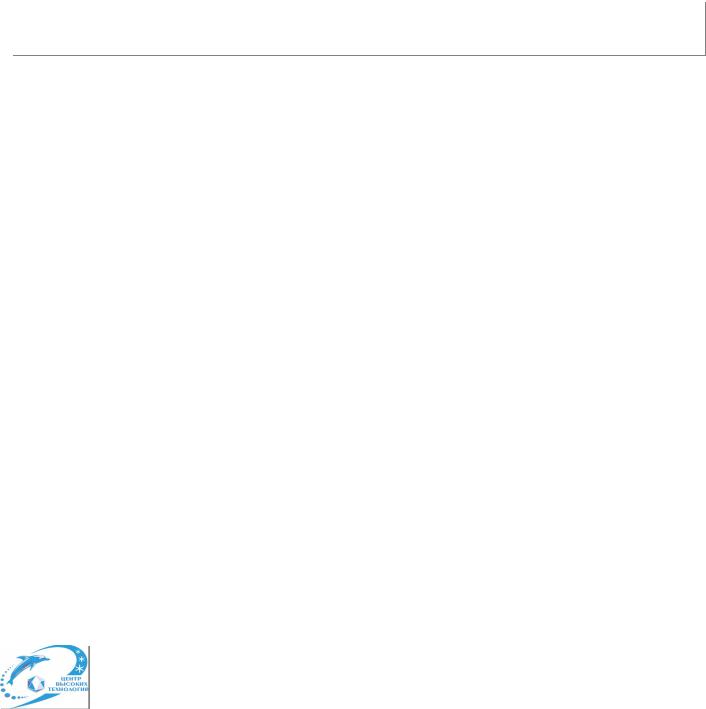
3. Гидродинамика вязкой жидкости

Обратимся к случаю, когда необходимо учитывать процессы диссипации в жидкости. В реальных жидкостях всегда имеет место термодинамическая необратимость, связанная с наличием эффектов внутреннего трения (вязкости) и переноса тепла(теплопроводности).

Понятно, что полученные ранее уравнения гидродинамики идеальной жидкости не содержат подобных эффектов (это относится только к уравнению Эйлера – уравнение неразрывности сохраняет свою силу).

Вывод уравнения для учета потерь от внутреннего трения основывается на следующих соображениях. Наличие внутреннего трения (вязкости) проявляется в наличии дополнительного (необратимого) переноса импульса из мест с большей скоростью в места с меньшей скоростью.

Формально, необходимо дополнить поток импульса для идеальной жидкости необратимым термом, имеющим физический смысл необратимого переноса импульса (диссипации).

	ik p ik vi vk 'ik ik vi vk
где тензор	ik p ik 'ik	- называется тензором напряжений

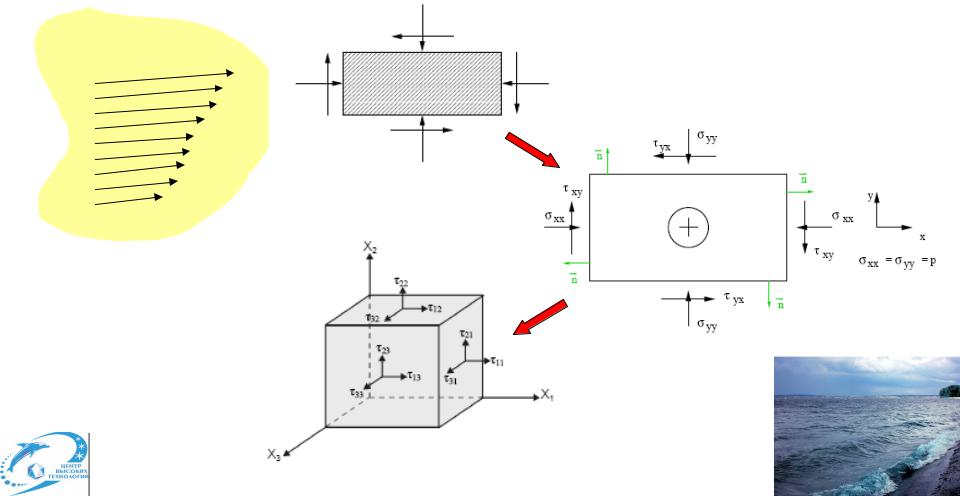
Как устроены нормальные и касательные компоненты тензора напряжений в жидкости?

Тензор ik'

носит название вязкого тензора напряжений.

Тензор ik определяет часть потока импульса, которая не связана с диссипацией

(обратимый перенос импульса)

Общий вид вязкого тензора напряжений можно установить на основе определенных соображений, справедливость которых может подтвердить только эксперимент.

Поле скоростей в жидкости

ik ik

3.1. Обобщенный закон Ньютона		vi
	ik :	vi
	ik :	x
		k
ik	неньютоновская вязкая жидкость
ik	(сложная реология)
	ньютоновская
	вязкая жидкость
	неньютоновская вязкая жидкость
	(сложная реология)
	vi / xk

3.2. Вывод уравнений вязкой жидкости

Для того, чтобы установить общий вид тензора вязких напряжений, используем следующие соображения:

• процессы внутреннего трения имеют место, если различные участки жидкости

движутся с различной скоростью – тензор вязких напряжений должен зависеть от
производных скорости жидкости по координатам	ik' : vi / x;k

•если градиенты скорости не очень велики, то можно, разложив тензор вязких напряжений в ряд по градиентам скоростей по координатам, оставить только первые члены (обобщенный закон Ньютона для сил трения в жидкости);

•члены, не зависящие от градиентов скоростей по координатам должны

отсутствовать в тензоре вязких напряжений, поскольку при v=const он должен

обращаться в нуль;

• тензор вязких напряжений должен быть симметричным, в силу изотропности

жидкости, поэтому единственными комбинациями первых производных от скорости жидкости по координатам могут быть суммы ( vi / xk ) ( vk / xi )

Общий вид тензора второго ранга, который удовлетворяет приведенным выше условиям, является:

vk 2

(3.1)

Здесь коэффициенты и , которые не зависят от скорости, называются

соответственно коэффициентами первой и второй вязкости. Обе эти величины всегда положительны.

Уравнение движения вязкой жидкости можно получить непосредственно прибавляя
в правую часть уравнения Эйлера величины	: ik' / xk

	(3.2)
	vl
	vl

	xl

Это наиболее общий закон движения вязкой жидкости; величины и вообще

говоря, могут зависеть от давления и температуры (вместе с последними величинами, коэффициенты вязкости могут меняться от точки к точке, поэтому не вынесены за знак производных).

Если коэффициенты вязкости постоянны вдоль жидкости, то можно получить следующее уравнение из (3.2):

(3.3) v

r r		r	+
(v )v	p v+		+
				3
				3

divv

- уравнение Навье-Стокса

(Навье – 1827г. – из модельных соображений; Стокс – 1845г. – приведение к современной форме)

Если жидкость несжимаема, тот уравнение Навье-Стокса сильно упрощается divv 0 :

r	r r	1		r	(3.4)
v
	(v )v		p	v


t

Тензор напряжений в несжимаемой жидкости принимает сравнительно простой вид:

C.L.Navier (1785-1836)

G.G.Stokes (1819-1903)



ik p ik	vi		vk		(3.5)

	x		x	i
		k

Таким образом, процессы диссипации (внутреннего трения) в несжимаемой жидкости описываются всего одним коэффициентом - коэффициентом динамической вязкости. Величина / - носит название кинематической

вязкости

Для несжимаемой жидкости, аналогично случаю уравнения Эйлера, можно исключить в уравнении Навье-Стокса давление. Применив операцию ротор к обеим частям уравнения (3.4), получим:

	r	r r	r
	rotv=rot vrotv rotv			(3.6)
t	rotv=rot vrotv rotv			(3.6)
t

Если распределение скоростей найдено, то давление находится из соотношения (оно получается применением к уравнению (3.4) операции дивергенция:

p	v	i	v		2 v	v	k
				k	i			(3.7)
	xk				xi xk
			xi

3.3. Граничные условия для вязкой жидкости

3.3.1. Кинематические граничные условия

На границе с твердым (неподвижным) телом из-за сил
межмолекулярного взаимодействия всегда должно быть
	r	0 (3.8)				vw
	v	0 (3.8)				vw
Таким образом, и нормальная и касательная			На подвижной твердой границе,
компоненты скорости на		неподвижной	На подвижной твердой границе,
твердой границе должны обращаться в нуль:			движущейся со скоростью:
r	r	(3.8а)	v	v		(3.8б)
vn	v 0	(3.8а)			w	(3.8б)

Условие равенства нулю касательной компоненты скорости в макроскопической гидродинамике носит название непроскальзывания (отсутствие скольжения на границе – no slip condition)

В микро- и наногидродинамике подобное условие может не выполняться !!!

3.3.2. Динамические граничные условия

Для сил на границе с жидкостью должны выполняться условия непрерывности; на границе раздела фаз должны выполняться условия равенства нормальных и касательных напряжений:

ii(1)	p(1)		(1)	(2)			p(1) p(2) p			(3.9)
ik(1)	ik(1) 1		ii	ii
ik(1)	ik(1) 1
		2		(1)		(2)			; i k	(3.10)
		2		ik	ik
ii(2)		p(2)
ii(2)		p(2)	межфазная					Общий вид капиллярного
	(2)	(2)	граница					(нормального) давления и
ik		ik	n p капиллярное (нормальное) давление					касательной компоненты
			ik ik касательная компонента					тензора напряжений на
									границе должен
								устанавливаться отдельно

Поучение 1. Уравнения Навье-Стокса в различных координатах А. Декартовы прямоугольные координаты:

vx v			x	vx
t				x
vy	v			vy
			x	x
t
vz v		x		vz
t				x

vx + vy +

x y

+vy

+vz vx z

+vz vy z

+vz vz z

Fx 1 p vx

Fy 1 p vy

Fz 1 p vz

Б. Цилиндрические координаты:

1 p

2 v

(v )vr

vr v

1 p

(v )v

1 p

(v )vz Fz

1 (r v

)

где (v )f=vr r

vz z

1 2

r r