1.2. Задание

Минимизировать функцию от 5-ти переменных Y=f(a, b, c, d, e) и реализовать ее в заданном элементном базисе. Функция, согласно варианту по номеру в списке студентов (журнале), выбирается в соответствии с табл. 1.1, базис реализации ­– из табл. 1.2.

N = (номер по журналу)/по модулю 6; M = (номер по журналу)/по модулю 4.

В табл. 1.1 в столбце «Функция» указаны значения входных переменных, при которых функция принимает единичное значение или ее значение неизвестно (*). Для остальных, не указанных явно значений входных переменных, функция принимает нулевое значение. Так, например, для N = 0, функция принимает единичное значение при abcde = 00000₂(0₁₀), abcde = 01000₂(8₁₀), abcde = 10000₂ (16₁₀) и т.д.

Табл. 1.1 ­– Выбор функции для реализации

N	Функция
0
1
2
3
4
5

Табл. 1.2 ­– Выбор базиса реализации функции

M	Базис
0	2ИЛИ-НЕ
1	2И-НЕ
2	3ИЛИ-НЕ
3	3И-НЕ

1.3. Пример выполнения работы

Пусть N = 0 

M = 1  базис 2И-НЕ.

Шаг 1. Минимизация заданной функции с использованием карты Карно на пять переменных (рис. 1.1).

Шаг 2. На основании рис. 1.1 получаем следующее выражение для функции Y:

.

Рис. 1.1 – Карта Карно для минимизации функции Y

Шаг 3. Используя законы де Моргана, приведем полученное выражение к заданному базису (2И-НЕ):

Шаг 3.Построим логическую схему, реализующую функцию Y:

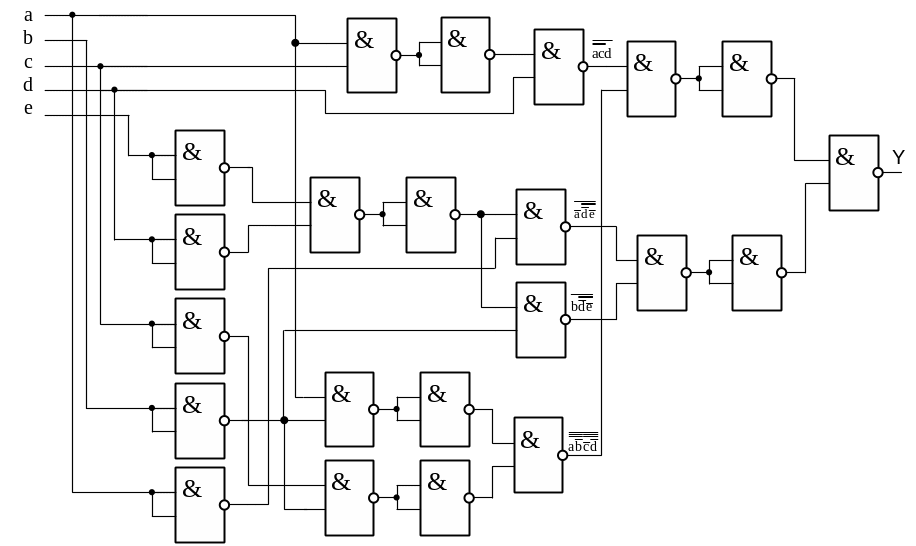
Рис. 1.2 – Логическая схема реализации функции Y в базисе 2И-НЕ

Определим основные параметры полученной схемы (без учета инверторов входных сигналов):

1. Число элементов в схеме N=17.

2. Число уровней схемы L=6.

3. Общее время задержки схемы – τ_сх =L * τ_эл-та = 6 * 10 нс = 60.

4. Цена по Квайну K=17 * 3 = 51.

4. . Содержание отчета

1. Задание согласно варианту.

2. Карта Карно для минимизации функции Y.

3. Выражение для функции Y в булевом базисе.

4. Выражение для функции Y в заданном базисе с описанием преобразований.

5. Логическая схема реализации функции Y в заданном базисе.

6. Вычисление основных параметров логической схемы.

Лабораторная работа №2 «Реализация сбф на дешифраторе»

2.1. Основные сведения

Дешифратор – устройство для преобразования двоичного позицион-ного кода в двоичный унитарный.

Пример позиционного кода:

N=5₁₀  R=]log₂5[=3 (бита)  Код (5)=101₂.

Позиционность: 101₂ = 1*2² + 0*2¹ + 1*2⁰ = 1 + 0 + 4 = 5₁₀.

Примеры унитарного кода:

КодУН (5) = 00001000 1 2 3 4 5 6 7 8	КодУН (2) = 01000000 1 2 3 4 5 6 7 8
КодУН (1,3,5) = 10101000 1 2 3 4 5 6 7 8	КодУН (2,3,4) = 01110000 1 2 3 4 5 ы6 7 8

Дешифраторы (DC) часто используются для преобразования двоичной информации в десятичную. Дешифраторы бывают двух типов:

1. Полные DC. В таких дешифраторах выполняется соотношение между числом входов и числом выходов N_вых=2^Nвх.

2. Неполные DC. Тогда выполняется соотношение 2^Nвх-1<N_вых<2^Nвх.

Например:

DC 416 – полный, 4 – кол-во входов, 16 – кол-во выходов.

DC 412 – неполный.

Условное графическое обозначение (УГО) дешифратора приведено на рис. 2.1.

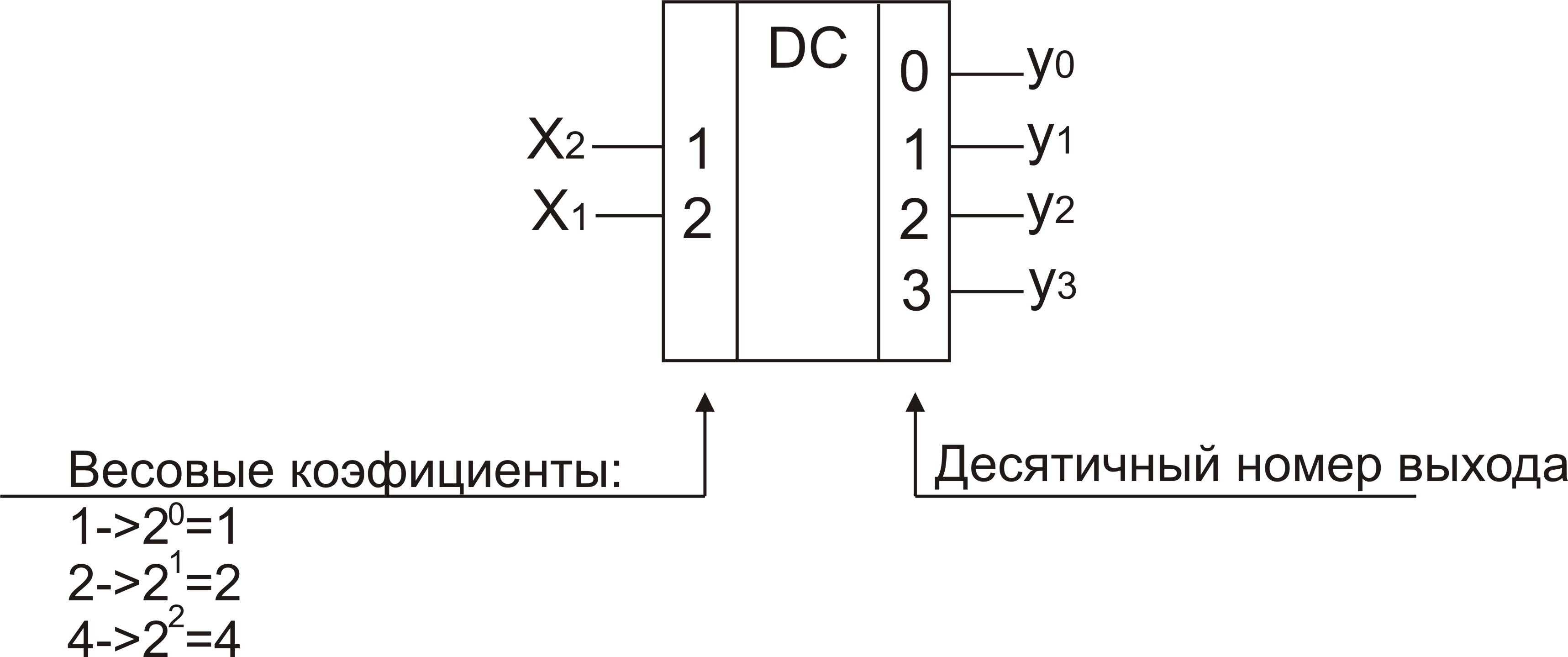
Рис. 2.1 – УГО дешифратора

Старший бит (в примере Х₁) подается на вход с большим весом (вход 2), а младший бит – соответственно, на вход с меньшим весом. Таблица истинности дешифратора:

Табл. 2.1 ­– Таблица истинности дешифратора 2 4

X1	X2	Y0	Y1	Y2	Y3
0	0	1	0	0	0
0	1	0	1	0	0
1	0	0	0	1	0
1	1	0	0	0	1