3. Побудова планів швидкостей

Побудову планів швидкостей розглянемо на прикладі 1-го положення механізму. З полюса р плану швидкостей за напрямом обертання кривошипа перпендикулярно ОА відкладаємо в масштабі вектор швидкості точки А, величина якого

м/c,

де - кутова швидкість кривошипа,

с^-1.

Приймаємо довжину відрізка, точки А, [ра] = 60 мм. Тоді масштаб плану швидкостей:

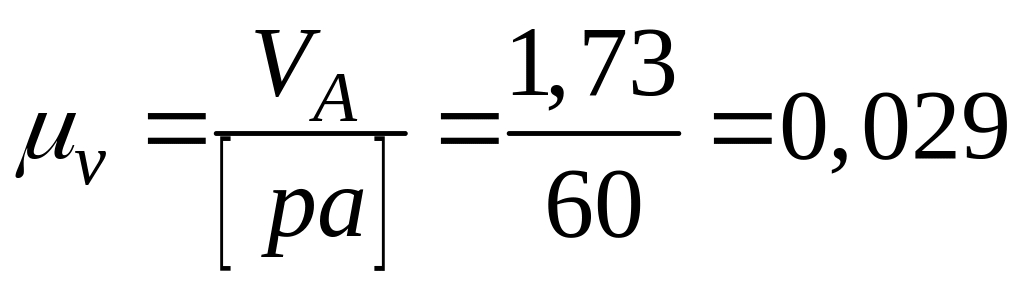м/(с^.мм).

Швидкість точки В визначаємо з рівнянь:

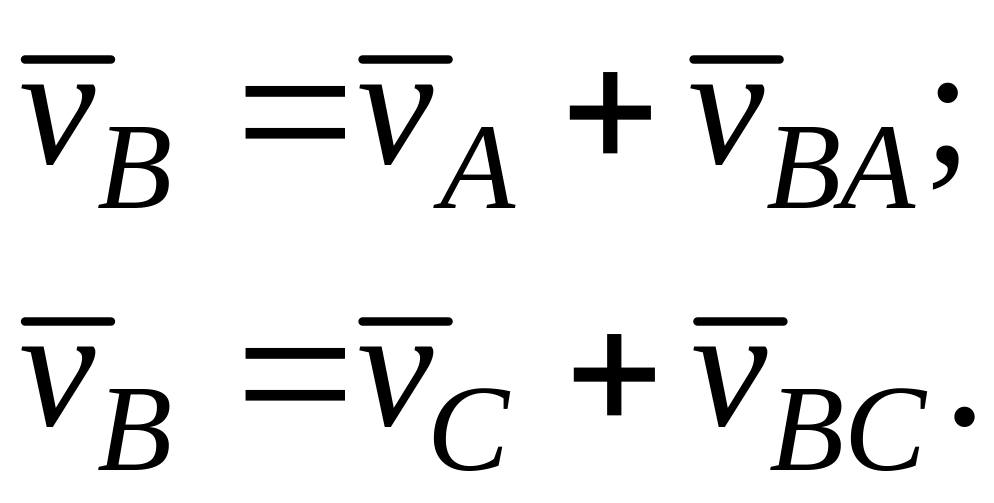
З точки р проводимо вектор відносної швидкості (перпендикулярно до АВ), а через те, що = 0, то з полюса р проводимо напрям вектора відносної швидкості (перпендикулярно ВС). Точка перетину цих ліній і є шукана точка b, а відрізки [pb] і [ab] відповідно у масштабі зображають вектори швидкостей і , тобто

м/с,

м/с.

Для визначення вектора швидкості точки D складаємо векторне рівняння:

.

На плані швидкостей через точку b проводимо вектор відносної швидкості (перпендикулярно BD), а через полюс р вектор швидкості (паралельно лінії руху повзуна). На перетині цих ліній знаходимо точку d.

Визначаємо швидкості:

м/с,

м/с.

Для визначення швидкостей центрів мас s₁, s_2, s₄ на плані швидкостей визначаємо за теоремою подібності склавши пропорції:

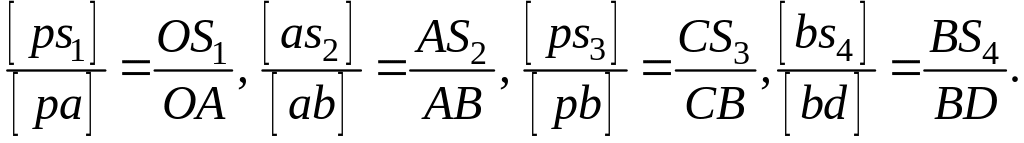
Знаходимо

мм,

мм,

мм,

мм.

З’єднуємо точки s₁, s_2, s_3, s₄ з полюсом плану швидкостей р, одержуємо відрізки , , , , які в масштабі визначають значення швидкостей центрів мас S ₁, S _2, S _3, S ₄:

м/с,

м/с,

м/с,

м/с,

м/с.

Значення кутової швидкості шатуна 2 знаходимо за формулою:

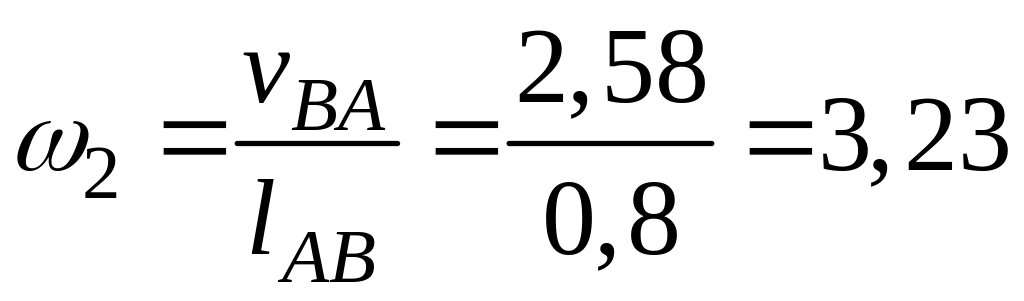с^-1.

Щоб визначити напрям кутової . Розглянемо обертання ланки 2 відносно точки А. Напрям руху точки В відносно точки А визначається вектором швидкості . Подумки переносимо цей вектор у точку В механізму і вважаємо точку А нерухомою. Отже, ланка 2 відносно точки А обертається проти руху годинникової стрілки.

Аналогічно визначаємо значення та напрямки кутових швидкостей ланок 3 і 4:

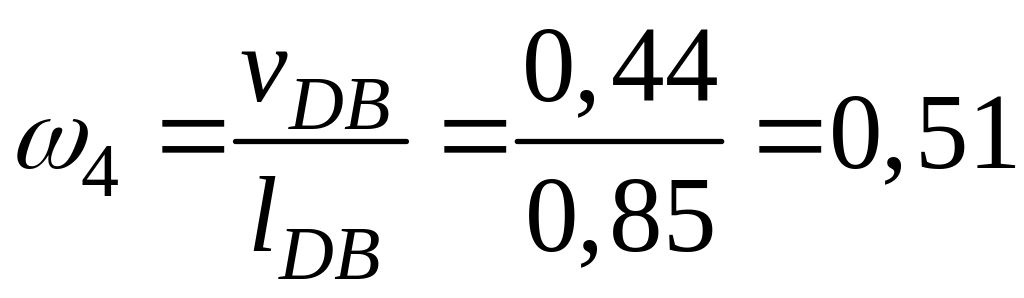с^-1,

с^-1.

Напрямки обертання ланок для першого положення механізму вказані дуговими стрілками на листі 1.

Плани швидкостей для інших положень механізму будуємо аналогічно. Отримані значення відрізків, які зображають вектори швидкостей, і значення швидкостей наведені в табл. 2.2.

2. Побудова планів прискорень

Побудову планів прискорень покажемо на прикладі першого положення механізму.

Визначимо прискорення точки А. Через те, що кривошип обертається рівномірно, точка А має тільки нормальне прискорення, яке напрямлене вздовж ланки АО до центра обертання. Значення цього прискорення

м/с².

Таблиця 2.2 Визначення швидкостей різних ланок і точок механізму

Позначення	Положення механізму
	0	1
ра, мм	60,0
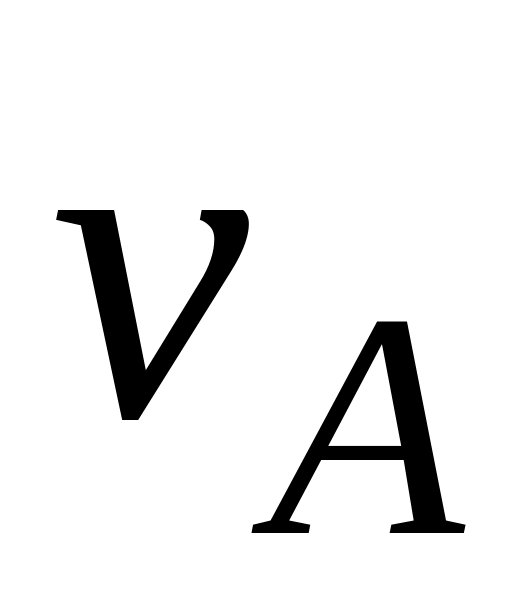, м/с	1,73
, мм	60,0	89,0
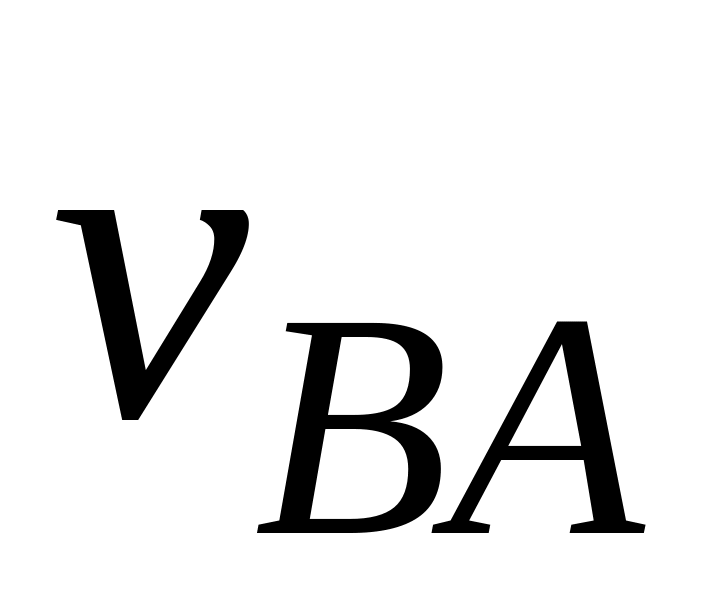. м/с	1,73	2,58
pb, мм	0	54,0
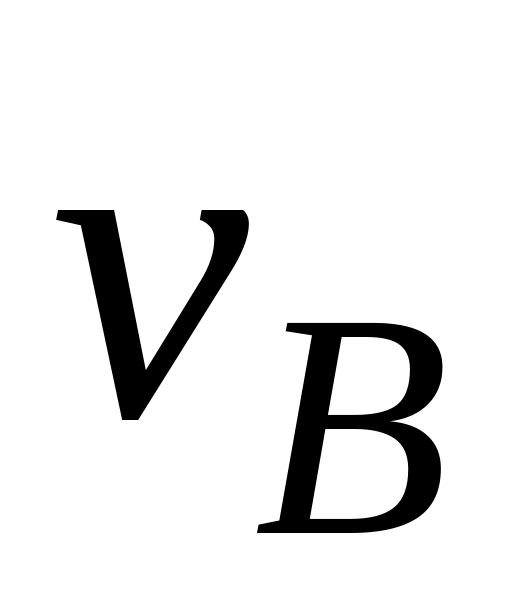, м/c	0	1,57
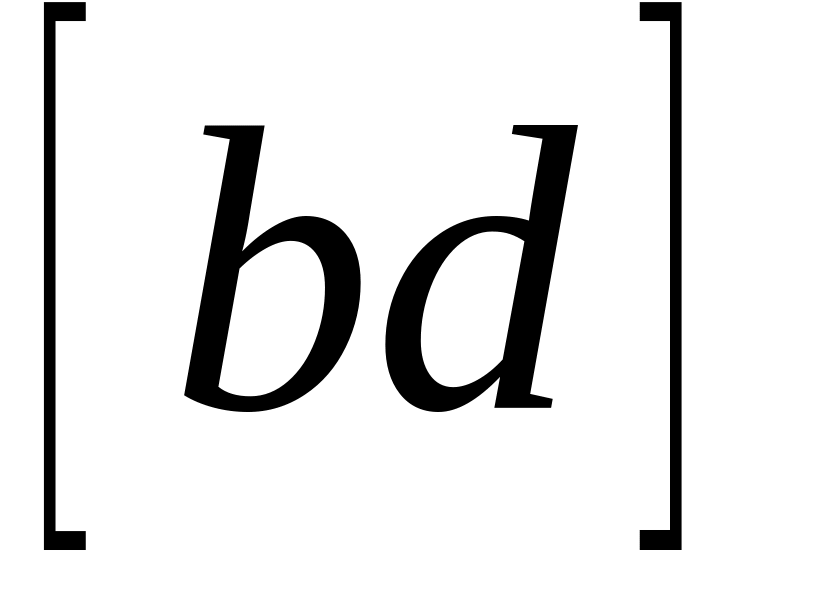, мм	0	15,0
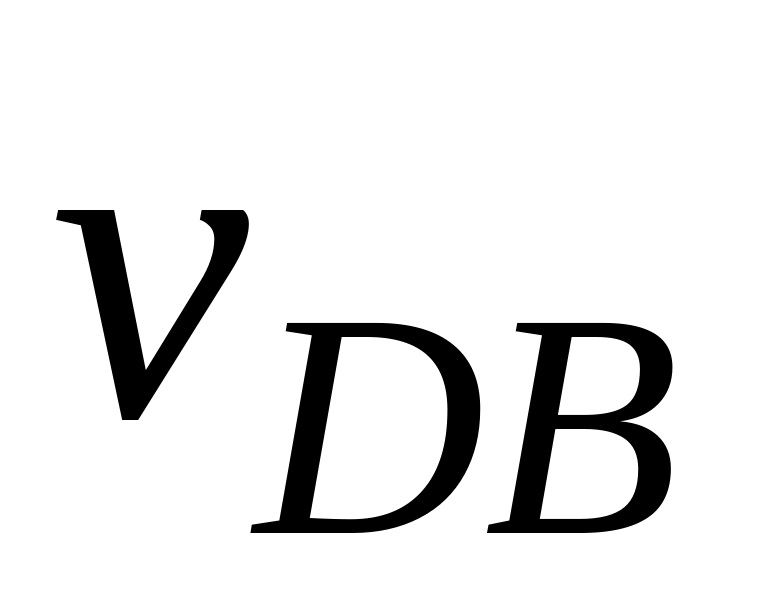, м/с	0	0,44
, мм	0	59,0
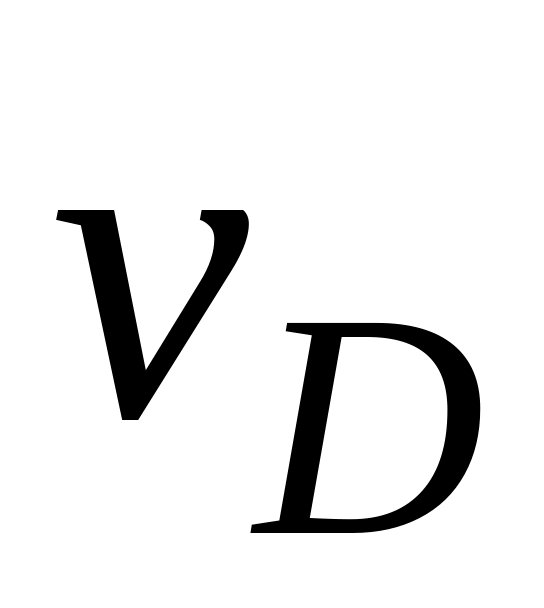, м/с	0	1,71
, мм	0,70
, мм	30,0	35,0
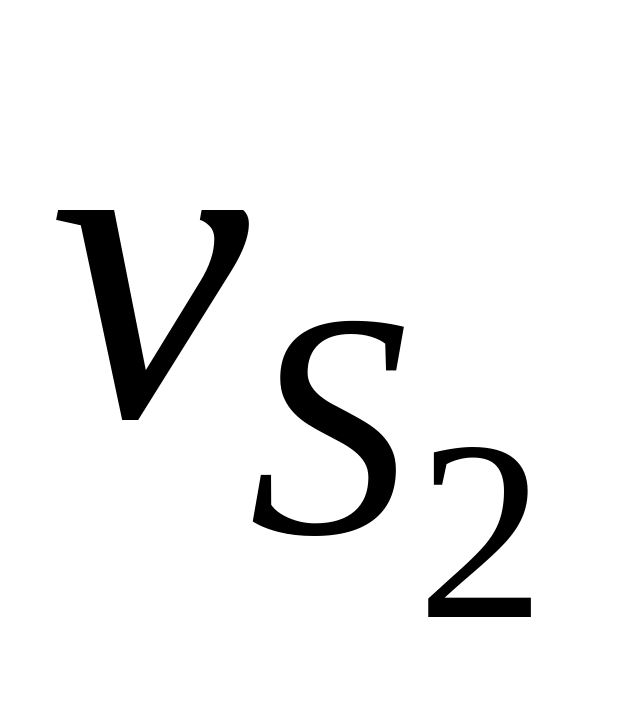, м/c	0,87	1,02
, мм	0	21,6
, м/c	0	0,63
, мм	0	57,0
, м/c	0	1,65
, с-1	2,16	3,23
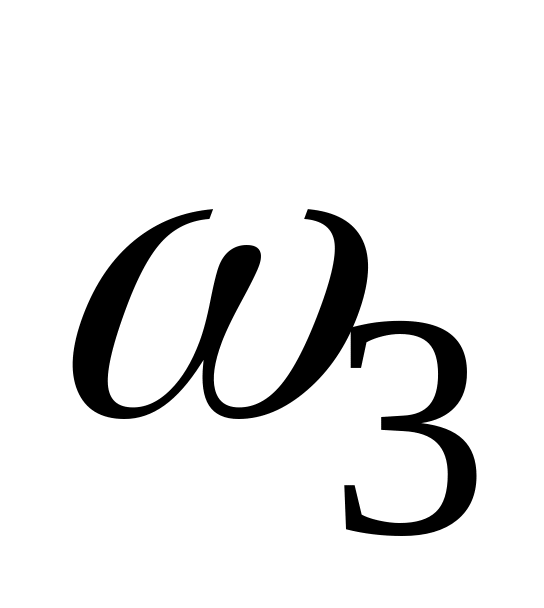, с-1	0	3,92
, с-1	0	0,51

Приймемо довжину відрізка , який зображає вектор прискорення точки А таким, що дорівнює 100 мм.

Тоді масштаб плану прискорень

м/(с²мм).

З довільної точки , яка прийнята за полюс плану прискорень, відкладаємо паралельно ланці ОА відрізок в напрямку від точки А до точки О.

Прискорення точок О і С дорівнюють нулю, отже, точки о і с збігаються з полюсом плану прискорень.

Прискорення точки В знаходимо, використовуючи наступні векторні рівняння:

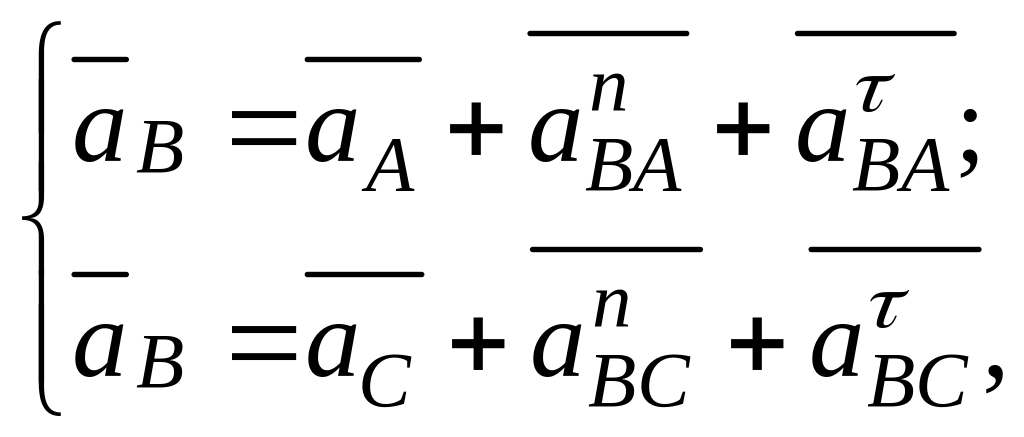
де - вектор нормального прискорення точки В при обертанні ланки 2 відносно точки А, має напрям уздовж ланки до умовного центру обертання; - вектор дотичного прискорення точки В при обертанні ланки 2 відносно точки А; - вектор нормального прискорення точки В при обертанні ланки 3 відносно точки С, має напрям уздовж ланки до центру обертання С; - вектор дотичного прискорення точки В при обертанні ланки 3 відносно точки С.

Визначаємо значення нормальних прискорень:

м/(с²мм),

м/(с²мм).

Тоді відрізки, що зображають їх на плані прискорень:

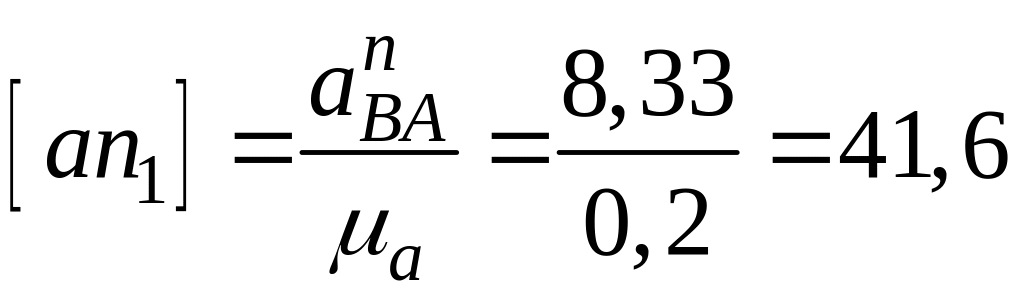мм,

мм.

Будуємо план прискорень і знаходимо прискорення точки В, а також невідомі складові і :

м/(с²мм),

м/(с²мм),

м/(с²мм).

Аналогічно, складаючи векторні рівняння, визначаємо прискорення точки D:

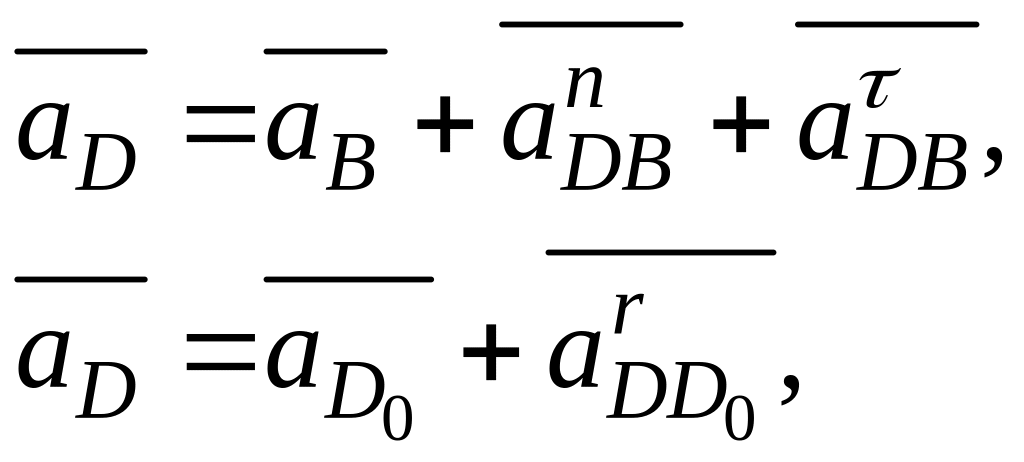
де - вектор нормального прискорення точки D при обертанні ланки 4 відносно точки B, що направлений вздовж ланки BD до умовного центру B; - вектор дотичного прискорення точки D при обертанні ланки 4 відносно точки B, = 0, - вектор відносного прискорення точки D відносно точки D₀, яка належить нерухомим напрямним.

Визначаємо величину нормального прискорення і відрізок, що зображає його на плані прискорень:

м/(с²мм),

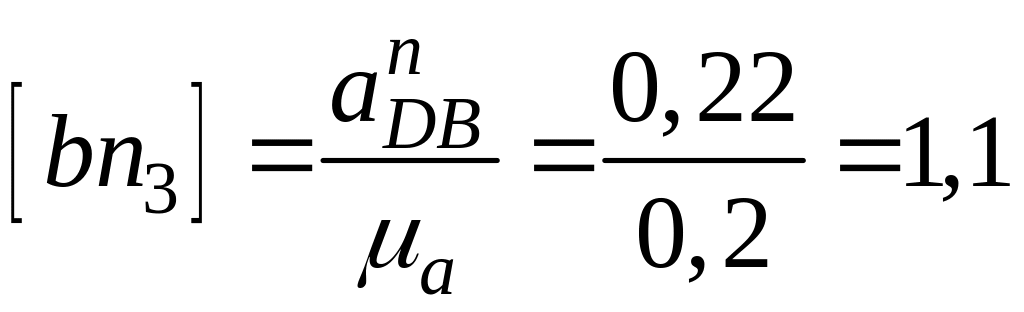мм (цим відрізком нехтуємо).

Будуємо план прискорень і визначаємо прискорення:

м/с²,

м/с²,

Використовуючи теорему подібності планів прискорень, знаходимо положення точок на плані прискорень, з’єднавши які з полюсом плану прискорень, визначаємо прискорення центрів мас S₁, S₂, S₃, S₄ ланок 1. 2, 3 і 4:

м/с²,

м/с²,

м/с²,

м/с²,

м/с².

Визначаємо кутові прискорення ланок:

, тому що ,

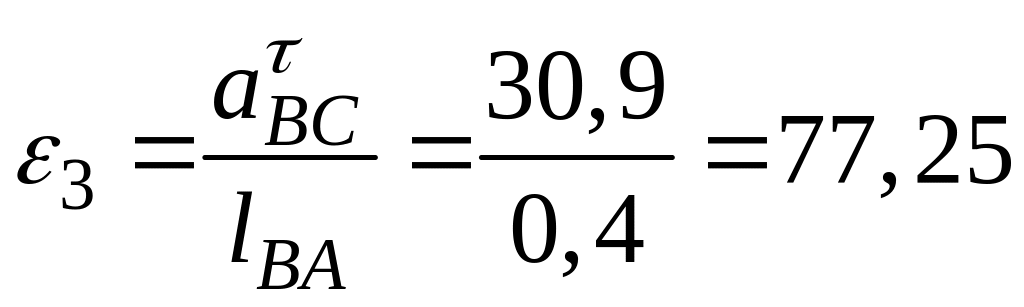с^-2,

с^-2,

с^-2.

Напрям кутового прискорення визначається напрямом дотичного прискорення. Щоб визначити напрямок кутового прискорення переносимо вектор в точку В. Розглядаємо рух ланки 2 відносно точки А. В нашому випадку направлено проти руху годинникової стрілки. Аналогічно отримаємо: - проти, - за годинниковою стрілкою. Напрямок кутових приско рень ланок в 1 положенні механізму зображено на листі 1 дуговими стрілками.

Отримані значення відрізків, які зображають вектори прискорень, та їх значення наведені в таблиці 2.3.

Таблиця 2.3 Визначення прискорень різних ланок і точок механізму

Позначення	Положення механізму
	0	1
, мм	100
, м/с2	19,91
, мм	18,9	41,6
, м/с2	3,78	8,33
, мм	132	40,0
, м/с2	26,4	8,0
, мм	173,0	154,5
, м/с2	34,6	30,9
, мм	0	30,6
, м/с2	0	6,13
, мм	173	157
, м/с2	34,6	31,5
, мм	0	1,11
, м/с2	0	0,22
, мм	63,0	11,0
, м/с2	12,6	22,0
, мм	196,0	162,0
, м/с2	39,2	32,4
, мм	40,0
, м/с2	8,0
, мм	128,0	128,0
, м/с2	25,6	25,6
, мм	68,5	63,0
, м/с2	13,7	12,6
, мм	184,0	160,0
, м/с2	36,8	32,0
, с-2	33,0	32,0
, с-2	86,5	77,25
, с-2	14,82	2,59