Методические указания к выполнению лабораторной работы №2 Обобщающие характеристики совокупности

Задание

Проанализировать полученные распределения трех признаков на основе известных статистических характеристик (для каждого признака):

1. характеристики центра распределения (среднее значение, мода, медиана);

2. характеристики структуры распределения (1 квартиль, 3 квартиль, 1 дециль, 9 дециль);

3. характеристики вариации (размах вариации, дисперсия, среднее квадратическое отклонение, среднее линейное отклонение, коэффициент вариации);

4. характеристики формы распределения (асимметрия, эксцесс).

Подготовка к выполнению лабораторной работы

1. По учебнику изучить темы:

• Средние величины

• Структурные характеристики распределения

• Показатели вариации

• Показатели формы распределения

2. Уметь рассчитывать необходимые для анализа распределения характеристики и интерпретировать полученные значения.

Выполнение задания в ППП MS Excel

Необходимые характеристики должны быть рассчитаны как для исходного ряда значений каждого признака (с помощью функций MS Excel), так и для сгруппированных данных. При этом последние являются приближенными значениями искомых характеристик.

1. Характеристики центра и структуры распределения

Средняя величина - обобщающая количественная характеристика признака в статистической совокупности, отражающая типичный уровень этого признака в расчете на единицу совокупности.

Средняя величина для несгруппированных данных:

,

где x_i – значение признака у i–ой единицы совокупности;

N - объем совокупности.

Среднее значение по исходным данным определяются с помощью функции СРЗНАЧ. Вызываем функцию (из категории «Статистические»):

= СРЗНАЧ(число_1;число_2…)

где число_1;число_2… – числовые аргументы, для которых вычисляется среднее (выделить для первого аргумента столбец исходных значений признака).

Средняя величина для интервально сгруппированных данных:

,

где х^н_j, х^в_j - нижняя и верхняя граница j–ого интервала;

k – число групп;

f_j – вес усреднения для j-ой группы (в качестве весов усреднения берут частоты/частости).

К структурным характеристикам ряда распределения относятся квантили распределения и мода.

Квантиль распределения (Q_i) – это значение признака, занимающее определенное место в упорядоченной по данному признаку совокупности. Основными квантильными характеристиками являются:

• медиана (Ме) - значение признака, приходящееся на середину упорядоченной совокупности,

• квартили (Q_1/4, Q_2/4=Ме, Q_3/4) – значения признака, делящие упорядоченную совокупность на 4 равные (по числу единиц) части,

• децили (Q_0,1,Q_0,2,…,Q_0,9) – значения признака, делящие упорядоченную совокупность на 10 равных частей.

Квантили для несгруппированных данных определяются по упорядоченным значениям механически, путем определения номера искомого наблюдения.

Квантили распределения по исходным данным определяются с помощью функций МЕДИАНА, КВАРТИЛЬ, ПРОЦЕНТИЛЬ. Вызываем необходимую функцию (из категории «Статистические»):

= МЕДИАНА(число_1;число_2…)

где число_1;число_2… – числовые аргументы, для которых вычисляется медиана (выделить для первого аргумента столбец исходных значений признака).

= КВАРТИЛЬ(массив;часть)

где массив – это столбец исходных значений признака, для которых определяется значение квартиля;

часть – это значение, определяющее уровень квартиля: для Q_1/4 – 1, для Q_3/4 - 3.

= ПРОЦЕНТИЛЬ(массив;К)

где массив – это столбец исходных значений признака, для которых определяется значение К-ого процентиля (может использоваться для определения квартилей и децилей);

К – это значение, определяющее уровень процентиля: для Q_0,1 – 0.1, для Q_0,9 – 0.9; для Q_1/4 – 0.25, для Q_3/4 – 0.75 .

Результаты расчета характеристик по функциям MS Excel:

Для сгруппированых данных предварительно определяется группа, которая содержит i-ый квантиль: та группа от начала ряда, в которой сумма накопленных частот равна или превышает N·i, где i- индекс квантиля.

Квантили для интервально сгруппированных данных:

где X_qi - нижняя граница интервала, в котором находится i - ый квантиль;

- величина интервала, в котором находится i - ый квантиль;

F_(-1) – сумма накопленных частот интервалов, предшествующих интервалу, в котором находится i - ый квантиль;

N_qi – частота интервала, в котором находится i - ый квантиль.

Мода (Мо) – наиболее часто встречающееся значение признака в совокупности.

Для не сгруппированных данных мода обычно не определяется. Если признак принимает ограниченное число значений и они повторяются, можно определить моду с помощью функции МОДА. Вызываем функцию (из категории «Статистические»):

= МОДА(число_1;число_2…)

где число_1;число_2… – числовые аргументы, для которых вычисляется мода (выделить для первого аргумента столбец исходных значений признака).

Для интервально сгруппированного ряда мода – это значение признака, которому соответствует наибольшая плотность распределения. Для сгруппированых данных предварительно определяется группа, которая содержит моду: та группа, которой соответствует максимальная частота/частость или плотность распределения (для не равноинтервальных – только по максимальной плотности). Далее значение моды уточняется по формуле:

где X_Mo - нижняя граница интервала, в котором находится мода;

- величина модального интервала;

N_Mо, N_Mо-1, N_Mо+1 – частоты, соответственно, модального, предшествующего и последующего интервалов.

Расчет моды по данной формуле предполагает, что модальный, предшествующий и последующий интервалы – это интервалы одинаковой длины.

Таблица 3. Расчет характеристик центра и структуры распределения

Границы интервала		Частота	Накопленная частота	Середина интервала	Сер. инт. Частота
нижняя	верхняя
50	150	12 Мо	12 Q1/4, Q1/10	100	1200
150	250	10	22 Ме	200	2000
250	350	8	30 Q3/4	300	2400
350	450	5	35	400	2000
450	550	4	39 Q9/10	500	2000
550	650	1	40	600	600
Итого		40	-	-	10200

Расчет характеристик (см. табл. 3):

Среднее: млн. у.е./год

Медиана: млн. у.е./год

1 квартиль: млн. у.е./год

3 квартиль: млн. у.е./год

1 дециль: 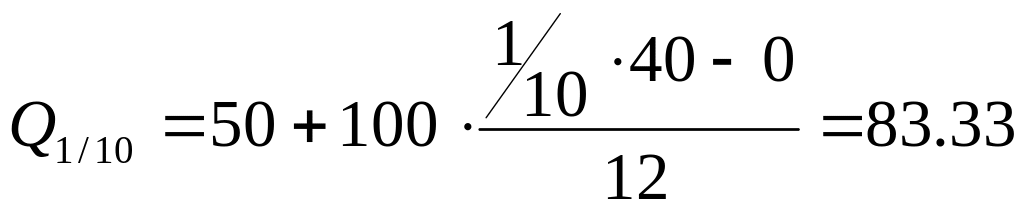млн. у.е./год

9 дециль: млн. у.е./год

Мода: млн. у.е./год

2. Характеристики вариации

Для измерения рассеяния (вариации) признака применяются различные абсолютные и относительные показатели вариации.

Абсолютные показатели вариации:

• Размах вариации, R - разность между максимальным и минимальным значениями признака в совокупности:

• Среднее линейное отклонение, d - средняя арифметическая абсолютных значений отклонений отдельных вариант от их средней арифметической. Для не сгруппированных и сгруппированных данных, соответственно:

, ,

где N – объем совокупности;

k - число групп;

f_j – частота/частость в j – ой группе.

• Среднее квадратическое отклонение,  - средняя квадратическая из отклонений отдельных вариант от их средней арифметической. Для не сгруппированных и сгруппированных данных, соответственно:

, .

• Дисперсия, ² - средний квадрат отклонений вариант от их средней величины (квадрат среднего квадратического отклонения). Может быть также вычислена, как разность среднего квадрата значения признака и квадрата среднего арифметического значения признака:

.

Абсолютные показатели вариации по исходным данным определяются с помощью функций СРОТКЛ, СТАНДОТКЛОН, ДИСП. Вызываем необходимую функцию (из категории «Статистические»):

= СРОТКЛ(число_1;число_2…)

где число_1;число_2… – числовые аргументы, для которых вычисляется среднее линейное отклонение (выделить для первого аргумента столбец исходных значений признака).

= СТАНДОТКЛОН(число_1;число_2…)

где число_1;число_2… – числовые аргументы, для которых вычисляется среднее квадратическое отклонение (выделить для первого аргумента столбец исходных значений признака).

= ДИСП(число_1;число_2…)

где число_1;число_2… – числовые аргументы, для которых вычисляется дисперсия (выделить для первого аргумента столбец исходных значений признака).

Самым распространенным относительным показателем рассеяния является коэффициент вариации. Он представляет собой выраженное в процентах отношение среднего квадратического отклонения к средней арифметической:

.

Коэффициент вариации используют как характеристику однородности совокупности. Совокупность считается качественно однородной, если коэффициент вариации не превышает 33%.

Результаты расчета характеристик по функциям MS Excel:

Расчет характеристик (см. табл. 4):

Размах вариации: млн. у.е./год

Среднее линейное отклонение: млн. у.е./год

Среднее квадратическое отклонение: млн. у.е./год

Дисперсия: (млн. у.е./год)²

Коэффициент вариации:

Таблица 4. Расчет показателей вариации

Серед. инт.	Частота	(Серед. инт.-сред.) Част.	ABS((Серед. инт.-сред.) Част.)	(Серед. инт.-сред.)2 Част.
100	12	-1860	1860	288300
200	10	-550	550	30250
300	8	360	360	16200
400	5	725	725	105125
500	4	980	980	240100
600	1	345	345	119025
Итого	40	0	4820	799000

3. Характеристики формы распределения

Для характеристики однородности совокупности используют и показатели формы распределения: коэффициент асимметрии и эксцесс.

Коэффициент асимметрии, As - показатель симметричности распределения. Положительная величина показателя асимметрии указывает на правостороннюю асимметрию, отрицательная – на левостороннюю, близость нулю свидетельствует о симметричном распределении.

Способы расчета коэффициента асимметрии:

1. Коэффициент асимметрии Пирсона:

.

Величина As может изменяться от –1 до +1 (для одновершинных распределений). Чем ближе по модулю As к 1, тем асимметрия существеннее.

2. Показатель, основанный на определении центрального момента третьего порядка – М3:

.

В симметричном распределении его величина равна нулю. Для оценки существенности такого коэффициента вычисляется его средняя квадратическая ошибка:

,

где N - объем совокупности.

Если As/_As меньше 2, это свидетельствует о несущественном характере асимметрии.

Коэффициент эксцесса, Ex - показатель островершинности распределения. Он рассчитывается для симметричных распределений. Эксцесс представляет собой выпад вершины эмпирического распределения вверх или вниз от вершины кривой нормального распределения. Показатель, использующий центральный момент четвертого порядка - М4:

.

Для нормального распределения эксцесс равен нулю. Положительный эксцесс означает, что распределение более островершинное чем нормальное; отрицательный эксцесс означает более плосковершинный характер распределения, чем у нормального Для оценки существенности такого коэффициента эксцесса вычисляется его средняя квадратическая ошибка:

,

где N - объем совокупности.

Если Ex/_Ex меньше 2, это свидетельствует о несущественном характере эксцесса (близости распределения по характеру островершинности к нормальному).

По исходным данным характеристики формы распределения могут быть определены с помощью функций СКОС, ЭКСЦЕСС. Вызываем функцию (из категории «Статистические»):

= СКОС(число_1;число_2…)

где число_1;число_2… – числовые аргументы, для которых вычисляется асимметрия (выделить для первого аргумента столбец исходных значений признака).

= ЭКСЦЕСС(число_1;число_2…)

где число_1;число_2… – числовые аргументы, для которых вычисляется эксцесс распределения (выделить для первого аргумента столбец исходных значений признака).

Результаты расчета характеристик по функциям MS Excel:

Таблица 5. Расчет показателей формы распределения

Середина интервала	Частота	(Середина интервала -среднее)Частота
100	12	-44686500
200	10	-1663750
300	8	729000
400	5	15243125
500	4	58824500
600	1	41063625
Итого	40	69510000

Расчет характеристик (см. табл. 5):

Асимметрия:

_{Так как данный ряд распределения явно несимметричен, расчет эксцесса не производится.}