Как вынести множитель из-под корня?

Разложить подкоренное выражение на множители и извлечь корни, которые извлекаются.

Раскладывать число на самые маленькие множители, а затем собирать в кучки одинаковые. Способ успешно применяется и при перемножении неудобных корней. Например, надо вычислить:

Арифметический квадратный корень обозначается  .

Например,

Обратите внимание:

1) Квадратный корень можно извлекать только из неотрицательных чисел

2) Выражение   всегда неотрицательно. Например,  .

Перечислим свойства арифметического квадратного корня:

1. 

2.  3. 

Запомним, что выражение   не равно  . Легко проверить:

 — получился другой ответ.

Кубический корень

Аналогично, кубический корень из   — это такое число, которое при возведении в третью степень дает число  .

Например,  , так как   ;

, так как  ;

, так как  .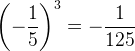

Обратите внимание, что корень третьей степени можно извлекать как из положительных, так и из отрицательных чисел.

Теперь мы можем дать определение корня  -ной степени для любого целого  .

Корень  -ной степени

Корень  -ной степени из числа   — это такое число, при возведении которого в  -ную степень получается число  .

Например,

Заметим, что корень третьей, пятой, девятой — словом, любой нечетной степени, — можно извлекать как из положительных, так и из отрицательных чисел.

Квадратный корень, а также корень четвертой, десятой, в общем, любой четной степени можно извлекать только из неотрицательных чисел.

Итак,   — такое число, что  . Оказывается, корни можно записывать в виде степеней с рациональным показателем. Это удобно.

По определению,

в общем случае  .

Сразу договоримся, что основание степени   больше  .

Например,

Выражение   по определению равно  .

При этом также выполняется условие, что   больше  .

Формула умножения корней позволяет: -умножать корни, -вносить число под корень, -сравнивать корни, -извлекать корни из больших чисел, -выносить множитель из-под корня.

Показательные выражения

Будем называть показательным выражением любую конструкцию вида a^k, где числа a и k — произвольные постоянные, причем a > 0. Методы работы с такими выражениями достаточно просты и рассматриваются на уроках алгебры 8-го класса.

Ниже приведены основные формулы, которые обязательно надо знать. Применение этих формул на практике, как правило, не вызывает проблем.

1. aⁿ · a^m = a^n + m;

2. aⁿ / a^m = a^n − m;

3. (aⁿ)^m = a^n · m;

4. (a · b)ⁿ = aⁿ · bⁿ;

5. (a : b)ⁿ = aⁿ : bⁿ.

Если встретилось сложное выражение со степенями, и не понятно, как к нему подступиться, используют универсальный прием — разложение на простые множители. В результате большие числа в основаниях степеней заменяются простыми и понятными элементами. Затем останется лишь применить указанные выше формулы — и задача будет решена.

• Задача. Найти значения выражений: 7⁹ · 3¹¹ : 21⁸, 24⁷ : 3⁶ : 16⁵, 30⁶ : 6⁵ : 25².

Решение. Разложим все основания степеней на простые множители: 7⁹ · 3¹¹ : 21⁸ = 7⁹ · 3¹¹ : (7 · 3)⁸ = 7⁹ · 3¹¹ : (7⁸ · 3⁸) = 7⁹ · 3¹¹ : 7⁸ : 3⁸ = 7 · 3³ = 189. 24⁷ : 3⁶ : 16⁵ = (3 · 2³)⁷ : 3⁶ : (2⁴)⁵ = 3⁷ · 2²¹ : 3⁶ : 2²⁰ = 3 · 2 = 6. 30⁶ : 6⁵ : 25² = (5 · 3 · 2)⁶ : (3 · 2)⁵ : (5²)² = 5⁶ · 3⁶ · 2⁶ : 3⁵ : 2⁵ : 5⁴ = 5² · 3 · 2 = 150.

Ответ: 189; 6; 150