
- •Составители: с.Н. Алексеенко, а.В. Романов
- •Глава 1. Криволинейные интегралы первого типа Масса материальной кривой
- •Определение криволинейного интеграла первого типа
- •Сведение криволинейного интеграла первого типа к обыкновенному определенному интегралу
- •Глава 2. Криволинейные интегралы второго типа Определение криволинейного интеграла второго типа
- •Существование и вычисление криволинейного интеграла второго типа
- •Случай замкнутого контура. Ориентация плоскости
- •Связь между криволинейными интегралами обоих типов
- •Глава 3. Основные свойства криволинейных интегралов Формула Грина
- •Вычисление площадей фигур с помощью криволинейного интеграла
- •Условия независимости криволинейного интеграла от пути интегрирования
- •Признак полного дифференциала
- •Восстановление функции по ее полному дифференциалу
- •Задача о работе плоского силового поля
- •Литература
- •Содержание
- •Глава 1. Криволинейные интегралы первого типа 3
- •Глава 2. Криволинейные интегралы второго типа 8
- •Глава 3. Основные свойства криволинейных интегралов 15
- •603950, Нижний Новгород,
- •603950, Нижний Новгород,
Министерство образования и науки РФ
Государственное образовательное учреждение
высшего профессионального образования
НИЖЕГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ
ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ им. Р.Е. Алексеева
Кафедра «Прикладная математика»
КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ ТЕОРИЯ
Нижний Новгород 2011
Составители: с.Н. Алексеенко, а.В. Романов
УДК 517
КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ТЕОРИЯ, ПРАКТИКА, ЗАДАНИЯ ДЛЯ РАСЧЕТНЫХ РАБОТ./НГТУ; cост.: С.Н. Алексеенко, А.В.Романов - Н. Новгород, 2011 – 45 с.
Научный редактор
Редактор С.Н. Митяков
Компьютерный набор: Т.О. Парфенова
Учебное пособие содержит подробное изложение лекционного материала по теории криволинейных интегралов.
Подписано в печать . Формат 60х84 1/16. Бумага газетная.
Печать офсетная. Усл. п. л. . Уч.-изд. л. . Тираж 300 экз. Заказ .
Нижегородский государственный технический университет.
Типография НГТУ.603950, Нижний Новгород, ул.Минина, 24. © Нижегородский государственный
технический университет
им. Р.Е. Алексеева, 2011
Глава 1. Криволинейные интегралы первого типа Масса материальной кривой
Пусть
на плоскости дана непрерывная незамкнутая
материальная кривая
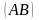 ,
причем известна линейная плоскость
,
причем известна линейная плоскость
 во
всех точках
во
всех точках
 кривой. Требуется определить массу m
всей кривой
.
кривой. Требуется определить массу m
всей кривой
.
Определение.
Линейной плотностью
называется предел, к которому стремится
отношение массы Δm,
дуги
 этой кривой, содержащей точку
,
т.е.
этой кривой, содержащей точку
,
т.е.
 ,
к длине дуги
,
при условии, что длина дуги
стремится к нулю.
,
к длине дуги
,
при условии, что длина дуги
стремится к нулю.
Для
решения поставленной задачи разобьем
произвольным образом на
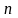 частей с помощью точек деления
частей с помощью точек деления
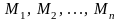 ,
которые пронумерованы в направлении
от
,
которые пронумерованы в направлении
от
 к
к

 .
Хотя можно было нумеровать их в обратном
направлении.
.
Хотя можно было нумеровать их в обратном
направлении.
Длину
дуги
 обозначим через
обозначим через
 .
На каждой частичной дуге
возьмем произвольно по точке
.
На каждой частичной дуге
возьмем произвольно по точке
 и во взятых точках вычислим значение
линейной плотности:
и во взятых точках вычислим значение
линейной плотности:
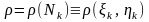 .
Если предложить, что плотность
.
Если предложить, что плотность
 во всех точках частичной дуги
постоянна и равна ее значению
во всех точках частичной дуги
постоянна и равна ее значению
 в точке
в точке
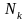 ,
то величина массы частичной дуги
будет:
,
то величина массы частичной дуги
будет:
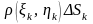 .
.
Масса
всей кривой
при сделанном допущении о постоянстве
плотности вдоль частичных дуг выразится
суммой:
 .
.
Поскольку
в действительности плотность распределения
массы на каждой частичной дуге
 ,
вообще говоря, непостоянна, то сумма
,
вообще говоря, непостоянна, то сумма
 не может быть принята за массу
.
Однако, если частичные дуги малы, то, в
силу непрерывности функции
не может быть принята за массу
.
Однако, если частичные дуги малы, то, в
силу непрерывности функции
 ,
значение плотности
в точках частичной дуги
будет мало отличаться от
,
значение плотности
в точках частичной дуги
будет мало отличаться от
 и масса
и масса
 будет близка к искомой массе
,
причем тем лучше, чем меньше длина
частичных дуг.
будет близка к искомой массе
,
причем тем лучше, чем меньше длина
частичных дуг.
Определение. Будем называть бесконечным уплотнением разбиения дуги последовательность разбиений дуги на частичные дуги (k = 1,…,n), когда каждая из частичных дуг бесконечно уменьшается по длине, а их число n неограниченно увеличивается. Обозначать это будем так: (AB)0.
Если
при бесконечном уплотнении разбиения
дуги (AB)
сумма
будет
стремиться к определенному пределу
 ,
не зависящему ни от способа разбиения
дуги
на частичные дуги
,
ни от выбора точек
на соответствующих частичных дугах, то
этот предел мы и будем принимать за
массу всей дуги
:
,
не зависящему ни от способа разбиения
дуги
на частичные дуги
,
ни от выбора точек
на соответствующих частичных дугах, то
этот предел мы и будем принимать за
массу всей дуги
:
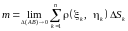 .
.
Определение криволинейного интеграла первого типа
Рассмотрим
произвольную функцию
 ,
определенную вдоль некоторой плоской
кривой
.
Разобьем
произвольным образом на
частей точками
,
считая
,
определенную вдоль некоторой плоской
кривой
.
Разобьем
произвольным образом на
частей точками
,
считая
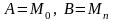 .
Длину дуги
обозначим через
.
Длину дуги
обозначим через
 .
На каждой частичной дуге
возьмем по произволу точку
.
На каждой частичной дуге
возьмем по произволу точку
 и, вычислив значение
и, вычислив значение
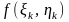 ,
составим сумму
,
составим сумму
 .
.
Она
называется интегральной суммой для
функции
,
заданной на кривой
.
Интегральная сумма
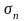 зависит от способа разбиения кривой
и выбора точек
на частичных дугах.
зависит от способа разбиения кривой
и выбора точек
на частичных дугах.
Определение. Если при бесконечном уплотнении разбиения дуги (AB) интегральная сумма имеет конечный предел, не зависящий ни от способа разбиения дуги на частичные дуги , ни от выбора точек на этих частичных дугах, то этот предел называется криволинейным интегралом первого типа от функции по кривой и обозначается
 .
.
Пользуясь
введенным определением, мы можем теперь
выражение для массы
кривой
записать в виде:
 ,
где
- линейная плотность кривой.
,
где
- линейная плотность кривой.
Отметим
особо, что величина криволинейного
интеграла первого типа не зависит от
направления интегрирования. Де5йствительно,
если при составлении интегральной суммы
мы будем производить нумерацию точек
деления кривой
в направлении от
к
(т.е. в обратном рассмотренному выше
направлению), то это не изменит интегральной
суммы, так как величины
 - длины дуг
обязательно положительные независимо
от того, какую точку дуги
мы считаем начальной, а какую – конечной.
Следовательно, не изменится и предел
интегральной суммы, т.е.
- длины дуг
обязательно положительные независимо
от того, какую точку дуги
мы считаем начальной, а какую – конечной.
Следовательно, не изменится и предел
интегральной суммы, т.е.
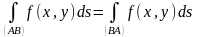 .
.
