Тема 2. Методи розв’язування задач лінійного програмування Лекція 3

• Графічне розв’язування задачі лінійного програмування

2.1. Графічне розв’язування злп

Числом ступенів свободи задач ЛП називається різниця між числом змінних і числом незалежних обмежень рівностей. Графічно можна розв’язати задачу з числом ступенів свободи меньше трьох.

Для графічного розв’язування ЗЛП необхідно:

1. Визначити число ступенів свободи ЗЛП.

2. Привести ЗЛП в однорідну форму з обмеженнями-нерівностями. Для цього слід отримати в системі обмежень-рівнянь одиничну підматрицю. Змінні, що відповідають стовпцям одиничної підматриці, утворюють базис і називаються базисними, інші змінні – вільними.

3. Вираз базисних змінних через вільні слід підставити в цільову функцію і записати обмеження-нерівноті типу “менше-рівно”, відкинувши базисні змінні.

4. Умови невід’ємності записати тільки для вільних змінних.

5. Побудувати область допустимих розв’язків системи обмежень для вільних змінних.

6. Визначити координати вершини ОДР, у якій цільова функція набуває екстремального значення.

Приклад 2.1

Розв’язати графічно ЗЛП:

(2.1)

при обмеженнях:

(2.2)

і умовах невід’ємності:

(2.3)

Приведемо в однорідну форму задачу (2.1) –(2.3). Випишемо матрицю коефіцієнтів та за допомогою елементарних перетворень утворимо одиничну підматрицю (віднімемо від першого рядка третій):



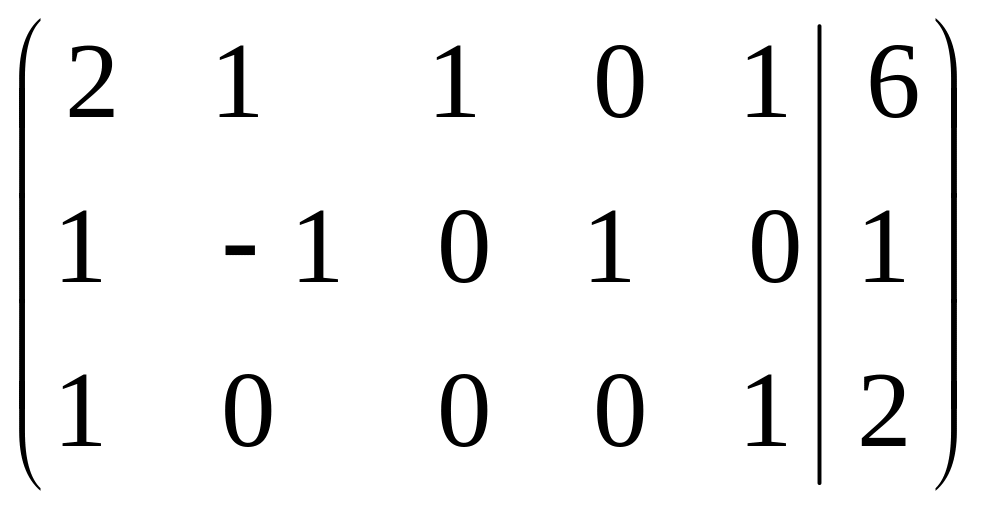
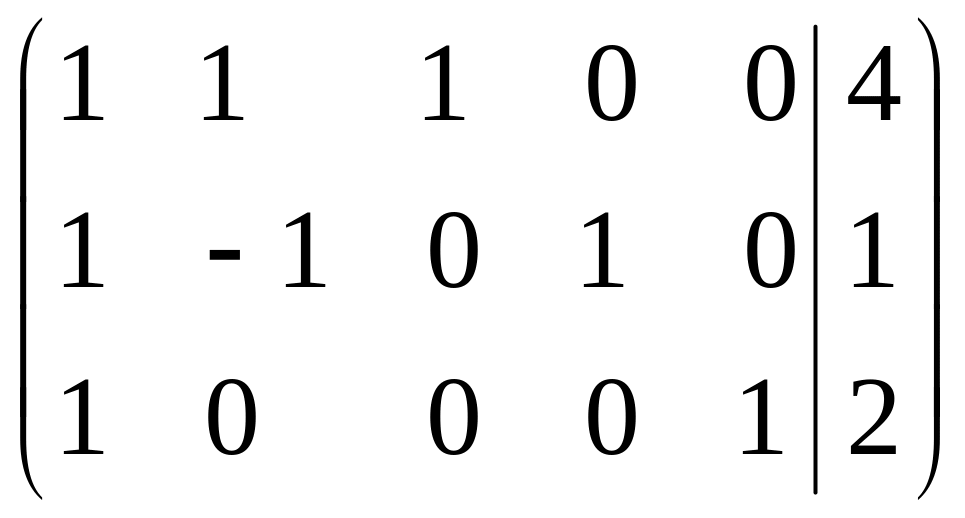
Отримаємо еквівалентну систему до системи (2.2)

( )

Очевидно, що одиничну підматрицю утворюють коефіцієнти при змінних . Отже, – базисні змінні, – вільні. Виразимо базисні змінні через вільні:

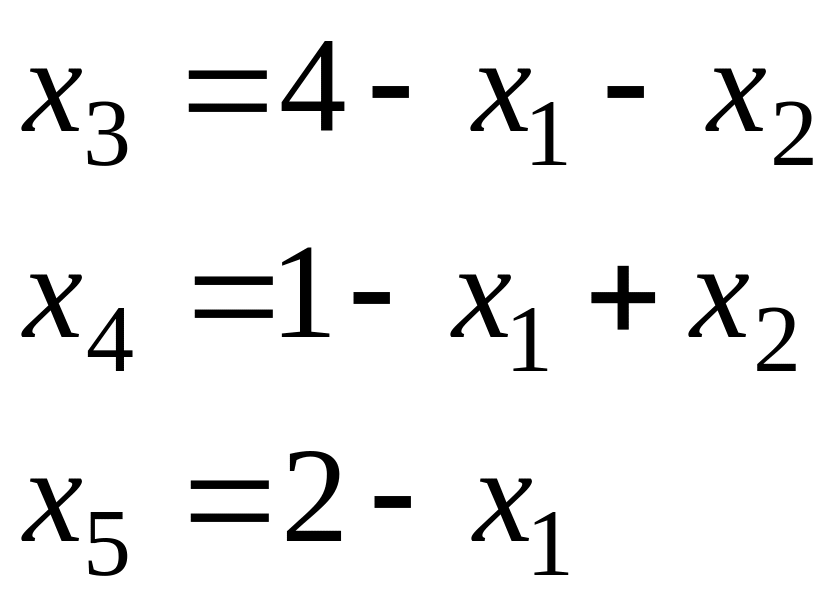
Використовуючи ці залежності виключимо базисні змінні з функціоналу, підставивши їх у вираз функціоналу:

,

тобто

Після відкидання базисних змінних в системі обмежень отримаємо наступну ЗЛП:

( )

( )

( )

Для графічного розв’язування задачі ( ) – ( ) необхідно

Побудуємо область допустимих розв’язків (ОДР) системи ( )

(рис. 2.1).

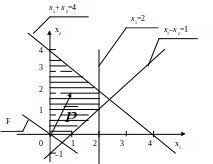
Досліджуючи будь-яку точку (як правило початок координат) з двох півплощин вибирають ту, в якій нерівність має місце. ОДР вибирають як загальну частину (перетин) всіх півплощин, що відповідають обмеженням та умовам невід’ємності.

Напрямок зростання цільової функції вказує її вектор-градієнт:

Для даної задачі . Отже .

Будуємо вектор і пряму, яка відповідає цільовій функції (вона перпендикулярна до вектора . Знаходимо опорну (оптимальну) точку в ОДР, врахувавши, що лінії рівня (прямі), на яких цільова функція постійна, перпендикулярна градієнту і при переміщенні лінії рівня паралельно самій собі в напрямку градієнта рівень (тобто значення F) збільшується.

Оптимальна точка , тобто .

Оптимальне значення цільової функції для задачі ( ) – ( ):

Повернувшись до задачі (2.1) – (2.3), отримаємо значення базисних змінних:

Отже оптимальна точка задачі (2.1) – (2.3): .

Оптимальне значення цільової функції задачі (2.1) – (2.3):

Висновок: задачу(2.1) – (2.3) можна звести до задачі ( ) – ( ) і розв’язати графічно.