3.6 Загальні аспекти інформованого пошуку

У попередньому розділі було показано, що в умовах відсутності інформації задача пошуку може бути вирішена успішно, але при цьому витрати часу і пам'яті можуть бути зовсім неприйнятними. Якщо задачу про ферзів спробувати вирішити на дошці 100 * 100, то кількість станів буде близько 10 ^ 400. Нехай вас не введе в оману компактна експоненціальна форма подання цього числа. Число атомів у видимій частині всесвіту становить близько 10 ^ 80.

У цьому зв'язку представляється доцільним поліпшити сліпий пошук в тих випадках, коли є яка-небудь додаткова інформація. Зрозуміло, ми не розглядаємо випадок, коли точно відомий шлях до мети. В останньому випадку задача вже вирішена. Йдеться про інформацію, яка спостерігається, але не дає прямої відповіді, як рухатися до мети.

Розглянемо наступну задачу. Нехай нам потрібно добратися з Таллінна до Москви повітряним транспортом. Відстані між містами і повітряні траси показані на ріс.12.6.

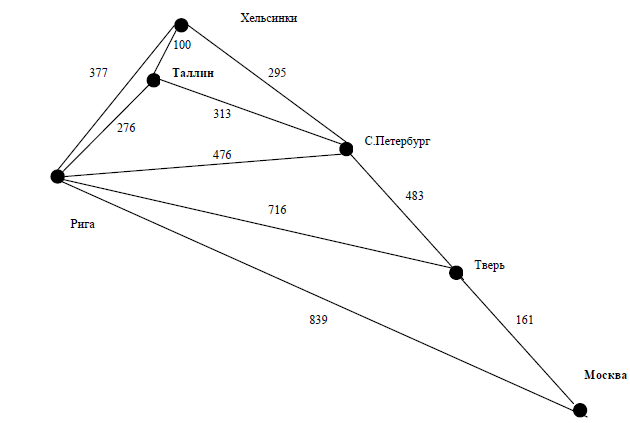
Рисунок 12.5 – Приклад трас до задачі пошуку

Якби ми не мали ніяких даних про відстані, то мав би місце сліпий (непоінформовані) пошук. Якщо ми знаємо тільки відстань від поточної точки до сусідніх, то ми в змозі виконати пошук за критерієм вартості. Найближчий пункт від Таллінна - Гельсінкі (100км), потім - Петербург (295), Рига (476), Твер (716), Москва (161). Загальна протяжність шляху - 1748 км, і вона суттєво відрізняється від оптимальної - 957 км. Припустимо, що нам відомо відстань від кожного з міст до Москви по прямій.

Ця інформація може використовуватися для вибору наступного пункту маршруту. Так, доступними пунктами з Таллінна є Хельсінкі (897км), С.Петербург (634) і Рига (839). Прагнучі на кожному кроці максимально наблизитися до мети, ми виберемо на першому кроці С.Петербург, на другому кроці - Твер, потім - Москву. Загальна протяжність шляху дорівнює оптимальної.

Даний вид пошуку називається жадібним пошуком по першій найкращій відповідності. Кожен наступний вузол для розгортання вибирається на основі функції оцінки f (n). У зв'язку з тим, що ми не володіємо точними оцінками, використовуються евристичні функції h (n) або евристики. У розглянутому прикладі евристична функція - це відстань до мети по прямій.

Рисунок 12.6 – Відстанні до пункта по прямій

Ця евристика не є свідомо оптимальної. Якщо, наприклад, між Твер'ю і Москвою літаки не літають, то оптимальний маршрут Таллінн - Рига - Москва буде істотно відрізнятися від запропонованого алгоритму жадібного пошуку по першому найкращому збігу: Таллінн - С.Петербург - Твер - Рига - Москва.

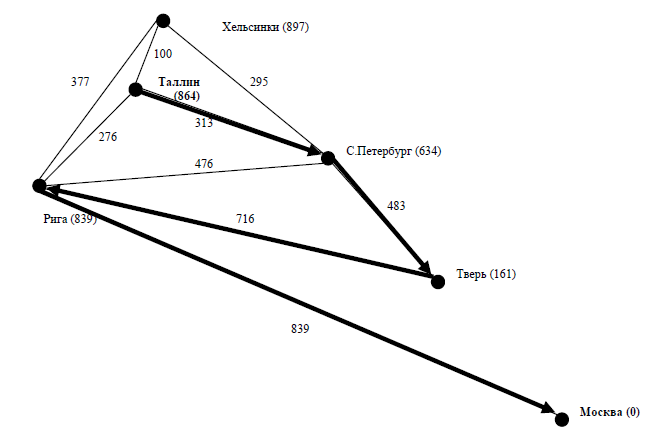
Рисунок 12.7 – Жадібний пошук по першій найкращій відповідності

Жадібний пошук по першій найкращій відповідності нагадує пошук в глибину і страждає від тих же недоліків. На останній схемі без запобігання повторюваних станів можливо нескінченне блукання по відрізку С.Петербург - Твер - С.Петербург і т.д. В найгіршому варіанті складність методу становить bm, де b - коефіцієнт розгалуження, m - максимальна глибина простору пошуку. Однак, гарна евристична функція дозволяє істотно знизити таку складність.