3.4 Пошук в глибину

При використанні формулювання задачі у вигляді простору станів може бути передбачено багато підходів до пошуку шляху вирішення. Двома основними стратегіями пошуку є пошук в глибину і пошук в ширину. У цьому розділі розглядаються стратегія пошуку в глибину і її варіант, званий ітеративним поглибленням.

Почнемо розробку даного алгоритму і його варіантів з аналізу описаної нижче простої ідеї.

Щоб знайти шлях вирішення Sol від заданого вузла N до деякого цільового вузла, необхідно реалізувати в програмі наступні операції:

• якщо N - цільовий вузол, то Sol = [N];

• інакше, якщо існує вузол-наступник N1 вузла N, такий, що мається шлях Sol від вузла N1 до цільового вузла, то Sol = [N | Sol].

Це формулювання може бути переведена на мову Prolog наступним чином:

Лістинг 12.1 ­– ­ Знаходження шляху від заданого вузла

solve(N,[N]) :-

goal ( N).

solve(K, [K | Soll]) :-

S < N , N1,

Solve (N, Soll)

По суті, ця програма являє собою реалізацію стратегії пошуку в глибину. Її називають пошуком в глибину з урахуванням того, в якому порядку розглядаються варіанти в просторі станів. Кожен раз, коли програмі пошуку в глибину надається можливість продовжити пошук шляхом переходу до одного з декількох вузлів, вона завжди віддає перевагу вибрати з них самий глибокий. Найглибшим вузлом є той, який розташований далі всіх, від початкового вузла. На рис. 12.4 показано, в якому порядку відвідуються вузли. Цей порядок відповідає трасуванні виконання програми Prolog при пошуку відповіді на наступне питання: ?- solve (a, Sol).

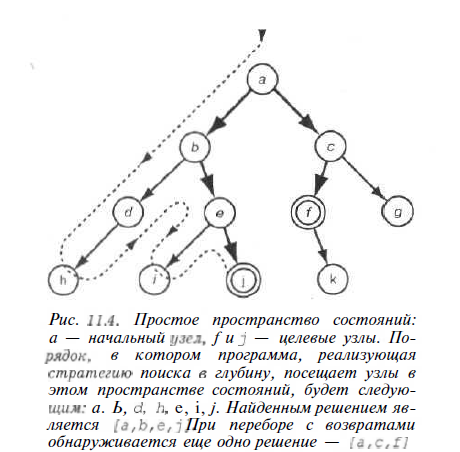
Рисунок 12.3 – Пошук в глибину

Пошук в глибину найбільшою мірою прийнятний для рекурсивного стилю програмування мовою Prolog. Причина цього полягає в тому, що сама система Prolog при виконанні мети перевіряє варіанти за принципом пошуку в глибину.

3.5 Пошук в ширину

На відміну від стратегії пошуку в глибину, стратегія пошуку в ширину передбачає відвідання в першу чергу тих вузлів, які є найближчими до початкового вузла. Це призводить до здійснення процесу пошуку, який, як правило, розвивається більшою мірою в ширину, ніж у глибину (рис. 12.5).

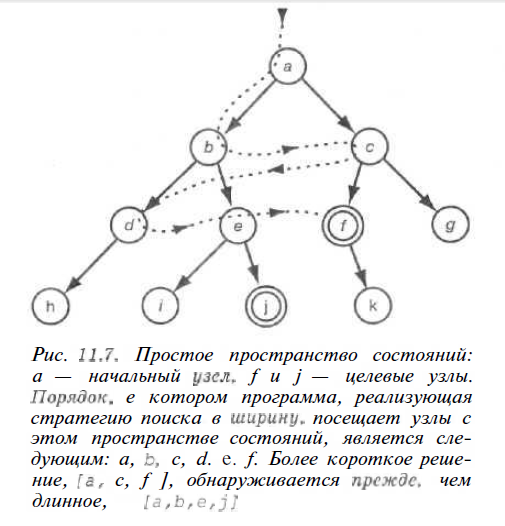
Рисунок 12.4 –Пошук в ширину

Складання програми пошуку в ширину складніше порівняно з пошуком в глибину. Причина такого ускладнення полягає в тому, що необхідно супроводжувати цілий безліч можливих альтернативних вузлів, а не розглядати тільки один вузол, як при пошуку в глибину. Таке безліч можливих вузлів являє собою цілу грань дерева пошуку, яка поступово зсувається вниз. Але навіть така безліч вузлів є недостатнім, якщо в процесі пошуку необхідно також виділити шлях до вирішення. Тому замість супроводу безлічі можливих вузлів доводиться супроводжувати безліч можливих шляхів.

Для представлення безлічі можливих шляхів буде використовуватися наступний спосіб: це безліч буде представлено як список шляхів, а кожен шлях - як список вузлів у зворотному порядку. Це означає, що голова а списку вузлів являє собою вузол, сформований в саму останню чергу, а останнім елементом у списку є початковий вузол пошуку.

Для здійснення пошуку в ширину по заданому безлічі можливих шляхів необхідно виконати наступні дії:

• якщо голова першого шляху являє собою цільовий вузол, то вважати цей шлях вирішенням завдання;

• в іншому випадку видалити перший шлях з безлічі можливих шляхів і сформувати безліч, що складається з усіх можливих однокрокових продовжень цього шляху, додати цю безліч продовжень до кінця множини можливих шляхів і виконати пошук в ширину на цій модифікованій множині.