Количественные методы прогнозирования

Количественные методы прогнозирования можно условно разделить на две подгруппы: анализ временных рядов и причинно-следственные методы. Количественные методы используют статистические данные прошлых периодов для построения прогнозов.

Прогнозирование по временным рядам

Временной ряд – это упорядоченные во времени наблюдения. Такие наблюдения проводятся через равные интервалы времени и фиксируют, к примеру, объемы отгрузок запаса в ответ на заявленный спрос на товарно-материальные ценности запаса [23, стр. 91]. На данный момент разработано довольно большое количество методов прогнозирования по временным рядам. При выборе модели прогнозирования фирме следует руководствоваться следующими данными:

1. Временной горизонт прогнозирования.

Выделяют краткосрочный, среднесрочный и долгосрочный горизонты прогнозирования. Модели краткосрочного прогноза усредняют случайные изменения и регулируют краткосрочные колебания (типа реакций потребителей на новое изделие). Среднесрочные прогнозы полезны при наличии сезонных колебаний, а модели долгосрочных прогнозов устанавливают общие тренды и особенно полезны в определении границ прогнозов.

2. Исходные данные.

3. Требуемая точность.

4. Бюджет, выделенный для разработки прогноза.

5. Уровень квалификации персонала.

Простейшей методикой прогнозирования по временным рядам является наивный прогноз. Она основывается на предположении, что прогнозируемое потребление будущего периода равно потреблению предшествующего периода. Возможна и модификация данного метода, к примеру, с учетом роста рынка. Тем не менее, данный метод совершенно не учитывает возможных колебаний, отклонений и тенденций спроса. При их наличии метод оказывается неэффективным, поскольку прогнозное значение всегда «запаздывает» по сравнению с реальным. Однако, несмотря на чрезмерную упрощенность, метод наивного прогноза имеет ряд преимуществ. Он не требует накопления существенной статистической базы. Наивный прогноз понятен, прост в подготовке, быстр в реализации, не требует фактически никаких затрат.

Следующим довольно распространенным видом прогнозирования является прогнозирование по средним значениям. Здесь традиционно выделяют метод простого и взвешенного скользящего среднего.

Метод простой средней

В случае если временной ряд имеет интервал наблюдений в один месяц, повысить точность наивного прогноза можно с помощью метода прогнозирования по простой средней. К примеру, для прогнозирования потребности на февраль, берем данные за январь, умножаем на количество рабочих дней в январе и делим на количество дней в феврале.

Метод простого скользящего среднего

• Применяется для оперативного прогнозирования по временным рядам, не имеющим явно выраженного тренда и цикличности (имеются лишь случайные колебания);

• +Простота применения;

• -Равная значимость значений предыдущих периодов;

Для расчета данных на март берем данные за январь, умножаем на количество рабочих дней, берем данные за февраль и умножаем на количество рабочих дней. Складываем и делим пополам.

Метод взвешенного скользящего среднего

применяется для устранения недостатка метода простого скользящего среднего – игнорирования неравнозначности сглаживаемых усреднением данных. Эта неравнозначность учитывается с помощью введения весовых коэффициентов, в сумме составляющих единицу. Обычно, как уже говорилось, больший вес получают более поздние периоды, приближенные к прогнозному. Сглаживание усреднением выполняется по формуле:

• Данный метод применяется для оперативного адаптивного прогнозирования.

Так же как и в простом скользящем, только каждое составялющая умножается на коэффициент, а потом вся сумма делится на сумму коэффициентов: (январь*раб дни*1+февраль*раб дни*2+ март*раб дни*3)/1+2+3

Экспоненциальное сглаживание

В этом методе каждый новый прогноз основан на учете значения предыдущего прогноза и его отклонения от фактического значения.

• Применяется для прогнозирования по временным рядам, обладающим сезонностью;

• Сглаживание производится с помощью двух коэффициентов: α для данных (указывает на важность последних значений) и γ для оценки сезонности;

Метод Хольта

• Применяется для прогнозирования по временным рядам с явно выраженными трендами.

• Сглаживание производится с помощью двух коэффициентов: α для данных (указывает на важность последних значений) и β для оценки тренда.

Метод Уинтера

• Применяется для прогнозирования по временным рядам, с явно выраженными трендом и цикличностью процесса;

• Сглаживание производится с помощью трех коэффициентов: α для данных, β для оценки тренда и γ для оценки сезонности.

Метод Кростона

• Применяется для прогноза объема продаж товаров, имеющих «прерывистый» спрос;

• Представляет собой двойное экспоненциальное сглаживание с одним коэффициентом α: пересмотр значений коэффициента α по завершении каждого прогнозного периода.

Причинно-следственные методы прогнозирования

Причинно-следственные (каузальные) методы прогнозирования основаны на регрессионной оценке объема продаж по каждой единице хранения с учетом влияния независимых факторов. К наиболее распространенным каузальным методам относится корреляционно-регрессионный анализ. Рассмотрим две разновидности данного метода – простую линейную регрессию и множественную регрессию.

Простая линейная регрессия

– прямая наилучшего приближения, для которой принимает наименьшее значение сумма квадратов расстояний от точек (x, y) из данного набора данных до этой прямой, измеренных в вертикальном направлении (по оси Y) [25, c. 431].

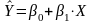
_где

-свободный член;

-угловой коэффициент;

X-независимая переменная;

Y- прогноз зависимой переменной.

Недостатком простой линейной регрессии считается то, что на практике большинство взаимосвязей требует изучения зависимости между искомой переменной и несколькими, а не одной независимой переменной. В этом случае предпочтительнее использовать множественную регрессию. Её уравнение имеет следующий вид:

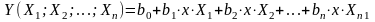(2.18)

Где Y-зависимая переменная

X₁; X₂; ...; X_{n –}независимые переменные

b₀; b_1; b₂; ...; b_n-коэффициенты регрессии

При использовании множественной регрессии особо остро встает проблема выбора независимых переменных. Необходимо так подобрать независимые переменные, чтобы исключить взаимную корреляцию между ними. Для этого строятся специальные корреляционные матрицы, и на их основе принимается решение о включении или же нет той или иной переменной.