
Шпора (Word)
.doc№1. Предел функции в точке. Единственность предела. Ограниченность функции, имеющей предел. Связь функции, имеющей предел, и бесконечно малой функции.
Рассмотрим функцию
![]() определенную в окрестности т.
определенную в окрестности т.
![]() ,
за исключением может быть самой т.
,
за исключением может быть самой т.
![]() .
.
![]() :
Число
:
Число
![]() называется пределом функции
называется пределом функции
![]() при
при
![]() ,
если
,
если
![]() ,
,
![]() ,
т.ч.
,
т.ч.
![]() ,
,
![]() (
(![]() ):
(выполнено)
):
(выполнено)
![]() .
.
Теорема: Если функция
![]() имеет в т.
имеет в т.
![]() предел, то он единственен.
предел, то он единственен.
Доказательство. Пусть существуют
![]() и
и
![]() ,
для
,
для
![]() ,
,
![]() .
Тогда
.
Тогда
![]() ,
,
![]() ,
т.ч.
,
т.ч.
![]() ,
,
![]() :
:
![]() ,
т.е.
,
т.е.
![]()
![]() ,
т.е.
,
т.е.
![]()
Т.к.
![]() - любое число, выберем
- любое число, выберем
![]() (предполагаем
(предполагаем
![]() ).
Тогда:
).
Тогда:
![]() ,
,
![]() ,
т.е.
,
т.е.
![]() .
Такого быть не может, следовательно
наше предположение не верно, т.е.
.
Такого быть не может, следовательно
наше предположение не верно, т.е.
![]() .
.
Функция
![]() называется ограниченной на
называется ограниченной на
![]() ,
если
,
если
![]() ,
,
![]() ,
т.ч.
,
т.ч.
![]()
Теорема: Если функция
![]() имеет в т.
имеет в т.
![]() предел, то она ограничена в этой т.
предел, то она ограничена в этой т.
***
Функция
![]() называется бесконечно малой, если
называется бесконечно малой, если
![]() ,
т.е.
,
т.е.
![]() ,
,
![]() ,
т.ч.
,
т.ч.
![]() ,
,
![]() :
:
![]() .
.
Теорема (асимптотическое разложение
функции, имеющей предел). Пусть
![]() .
Тогда в окрестности т.
.
Тогда в окрестности т.
![]() ,
функция
,
функция
![]() представима в виде:
представима в виде:
![]() ,
где
,
где
![]() - б/м при
- б/м при
![]() .
.
Доказательство.
![]() :
:
![]() ,
,
![]() ,
т.ч.
,
т.ч.
![]() ,
,
![]() :
:
![]()
![]() :
:
![]() ,
,
![]() ,
т.ч.
,
т.ч.
![]() ,
,
![]() :
:
![]()
Следовательно,
![]() ,
по определению
,
по определению
№2. Свойства б/м функций. Предел суммы, произведения и частного. Переход к пределу в неравенствах, предел промежуточной функции.
Функция
![]() называется бесконечно малой, если
называется бесконечно малой, если
![]() ,
т.е.
,
т.е.
![]() ,
,
![]() ,
т.ч.
,
т.ч.
![]() ,
,
![]() :
:
![]() .
.
Свойства:
1)
![]() - б/м при
- б/м при
![]() ,
,
![]() - число:
- число:
![]() - б/м при
- б/м при
![]()
Пусть
![]() ,
тогда
,
тогда
![]() .
Выберем
.
Выберем
![]() ,
,
![]()
![]() .
.
2)
![]() и
и
![]() б/м при
б/м при
![]() ,
,
![]() - тоже б/м при
- тоже б/м при
![]()
Пусть![]() ,
,
![]() . Тогда
. Тогда
![]() ,
т.е.
,
т.е.
![]() .
.
3)
![]() и
и
![]() б/м при
б/м при
![]() ,
,
![]() - тоже б/м при
- тоже б/м при
![]()
Пусть
![]() ,
,
![]() .
Тогда
.
Тогда
![]() ,
т.е.
,
т.е.
![]()
4)
![]() - б/м при
- б/м при
![]() ,
a
,
a
![]() ограниченная
ограниченная
![]() - б/м при
- б/м при
![]()
Пусть
![]() ,
,
![]() .
Выберем
.
Выберем
![]() ,
,
![]()
![]() ,
,
![]()
Пусть существуют конечные пределы
![]() ,
,
![]() .
Тогда:
.
Тогда:
![]()
Пусть
![]() ,
,
![]() .
Тогда по теореме об асимптотическом
разложении:
.
Тогда по теореме об асимптотическом
разложении:
![]() ,
,
![]() .
Тогда
.
Тогда
![]() .
Обозначим
.
Обозначим
![]() ,
,
![]() ,
,
![]() .
Тогда,
.
Тогда,
![]() ,
т.е.
,
т.е.
![]() ,
,
![]()
![]() .
.
![]()
Пусть
![]() ,
,
![]() .
Тогда по теореме об асимптотическом
разложении:
.
Тогда по теореме об асимптотическом
разложении:
![]() ,
,
![]() .
Тогда
.
Тогда
![]() ,
,
![]()
![]() .
Обозначим
.
Обозначим
![]() ,
,
![]() ,
,
![]() .
Тогда,
.
Тогда,
![]() ,
т.е
,
т.е
![]() ,
,
![]()
![]() .
.
 ,
,
![]()
Пусть
![]() ,
,
![]() .
Тогда по теореме об асимптотическом
разложении:
.
Тогда по теореме об асимптотическом
разложении:
![]() ,
,
![]() .
Тогда
.
Тогда
 ,
,
 .
Обозначим
.
Обозначим
![]() ,
,
![]() ,
,
 .
Тогда,
.
Тогда,
![]() ,
т.е.
,
т.е.
![]() ,
,
![]()
![]() .
.
Теорема (о переходе к пределу в
неравенствах): Пусть существуют
конечные пределы в некоторой окрестности
т.
![]()
![]() ,
,
![]() .
Тогда: если
.
Тогда: если
![]() ,
то
,
то
![]() .
.
Доказательство.
![]() ,
,
![]() ,
тогда:
,
тогда:
![]() ,
,
![]()
Теорема (о пределе промежуточной
функции): Если
![]() в некоторой окрестности т.
в некоторой окрестности т.
![]() и
и
![]() ,
то
,
то
![]() .
.
Доказательство. Пусть
![]() ,
тогда по теореме о переходе к пределу
в неравенствах:
,
тогда по теореме о переходе к пределу
в неравенствах:
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]()
![]() ,
,
Следовательно,
![]() и
и
![]() .
.
№3. Непрерывность функции в точке. Свойства непрерывных функций. Асимптотическое разложение непрерывной функции
Функция
![]() называется непрерывной в т.
называется непрерывной в т.
![]() ,
если
,
если
![]() .
.
Замечание: элементарные функции непрерывны в точках, где определены.
Теорема (о переходе к пределу, под
знаком непрерывности): Если функция
![]() непрерывна в т.
непрерывна в т.
![]() ,
то
,
то
![]() .
.
Доказательство. Т.к.
![]() и функция непрерывна, т.е.
и функция непрерывна, т.е.
![]() .
Следовательно
.
Следовательно
![]() .
.
Теорема (о непрерывности сложной
функции): Пусть
![]() непрерывна в т.
непрерывна в т.
![]() ,
а функция
,
а функция
![]() непрерывна в т.
непрерывна в т.
![]() .
Тогда сложная функция
.
Тогда сложная функция
![]() непрерывна в точке
непрерывна в точке
![]()
Доказательство.
![]()
Теорема: Пусть
![]() и
и
![]() непрерывны в т.
непрерывны в т.
![]() ,
тогда
,
тогда
![]() ,
,
![]() ,
,
![]() (
(![]() )
тоже непрерывны в этой точке.
)
тоже непрерывны в этой точке.
Доказательство: основано на свойствах
предела. Т.к. функция непрерывна, то
![]() .
.
Теорема (асимптотическое разложение
непрерывной функции): Если функция
![]() непрерывна в т.
непрерывна в т.
![]() ,
то в некоторой окрестности этой т.,
функция
,
то в некоторой окрестности этой т.,
функция
![]() представима в виде:
представима в виде:
![]() .
.
Доказательство. Рассмотрим
![]() .
По теореме об асимптотическом разложении
функции имеющей предел:
.
По теореме об асимптотическом разложении
функции имеющей предел:
![]() .
Т.к. функция непрерывна, то
.
Т.к. функция непрерывна, то
![]() ,
т.е.
,
т.е.
![]() .
.
№4. Эквивалентно бесконечно малые функции. Таблица эквивалентных б/м. Замена отношения б/м эквивалентными при вычислении пределов.
Функция
![]() называется бесконечно малой, если
называется бесконечно малой, если
![]() ,
т.е.
,
т.е.
![]() ,
,
![]() ,
т.ч.
,
т.ч.
![]() ,
,
![]() :
:
![]() .
.
Функции
![]() и
и
![]() называются эквивалентными б/м при
называются эквивалентными б/м при
![]() ,
если
,
если
![]() и обозначаются
и обозначаются
![]() .
.
Теорема: Для того, чтобы
![]() ,
необходимо и достаточно, чтобы
,
необходимо и достаточно, чтобы
![]() была б/м более высокого порядка чем
была б/м более высокого порядка чем
![]() и
и
![]() .
.
Доказательство.
Необходимость. Пусть
![]() ,
,
![]()
![]() .
По теореме об асимптотическом разложении
.
По теореме об асимптотическом разложении
![]() ,
где
,
где
![]() - б/м при
- б/м при
![]() .
Тогда,
.
Тогда,
![]() ,
,
![]() .
Рассмотрим
.
Рассмотрим
![]() ,
следовательно
,
следовательно
![]() .
Рассмотрим
.
Рассмотрим
![]() ,
,
![]()
![]() .
.
Достаточность. Пусть
![]() ,
,
![]()
![]() ,
,
 ,
,
![]() ,
,
![]() ,
,
![]()
![]() .
Пусть
.
Пусть
![]() ,
,
![]()
![]() ,
,
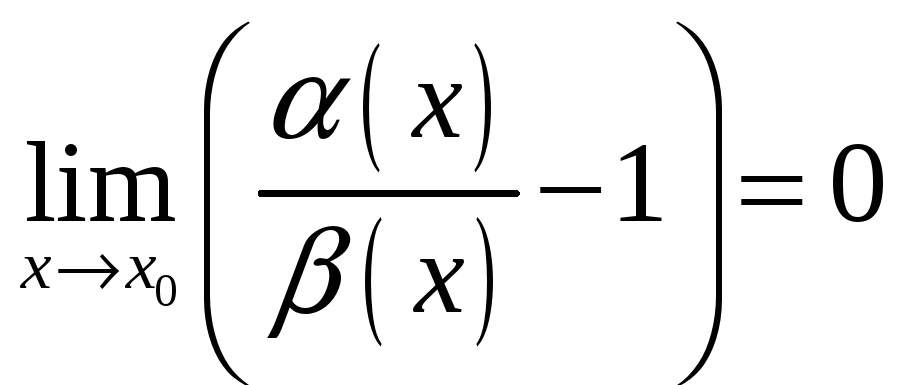 ,
,
![]() ,
,
![]() ,
,
![]()
![]() .
.
Таблица б/м
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Теорема (о замене б/м на эквивалентные
в отношениях): Пусть![]() ,
,
![]() эквивалентные б/м при
эквивалентные б/м при
![]() .
Тогда
.
Тогда
![]() .
.
Доказательство. Рассмотрим
![]() .
Тогда,
.
Тогда,
![]() .
.
№5. Сравнение б/м функций. Бесконечно большие функции, связь с б/м. Вертикальная асимптота графика.
Функция
![]() называется бесконечно малой, если
называется бесконечно малой, если
![]() ,
т.е.
,
т.е.
![]() ,
,
![]() ,
т.ч.
,
т.ч.
![]() ,
,
![]() :
:
![]() .
.
Пусть
![]() и
и
![]() б/м при
б/м при
![]() .
Тогда:
.
Тогда:
Если
![]() ,
то
,
то
![]() называется б/м более высокого порядка
чем
называется б/м более высокого порядка
чем
![]() ,
т.е.
,
т.е.
![]() ("о малое").
("о малое").
Если
![]() (числу), то
(числу), то
![]() и
и
![]() называется б/м одного порядка, т.е.
называется б/м одного порядка, т.е.
![]() ("о большое").
("о большое").
Если
![]() ,
то
,
то
![]() и
и
![]() называются эквивалентными б/м и
обозначаются
называются эквивалентными б/м и
обозначаются
![]() .
.
Функция
![]() называется б/б в т.
называется б/б в т.
![]() и обозначается
и обозначается
![]() ,
если
,
если
![]() ,
,
![]() ,
т.ч.
,
т.ч.
![]() ,
,
![]() :
:
![]() .
.
Теорема: Пусть
![]() б/б при
б/б при
![]() ,
тогда
,
тогда
![]() ,
б/м при
,
б/м при
![]() .
.
Доказательство.
![]() ,
,
![]() ,
т.ч.
,
т.ч.
![]() ,
,
![]() :
:
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]() ,
т.е.
,
т.е.
![]() ,
,
![]() ,
т.ч.
,
т.ч.
![]() ,
,
![]() :
:
![]() .
.
Выберем
![]() ,
т.е.
,
т.е.
![]() ,
,
![]()
![]() б/м при
б/м при
![]() .
.
Прямая на плоскости, к которой неограниченно приближается график функции, называется асимптотой графика.
Пусть
![]() б/б в т.
б/б в т.
![]() ,
тогда прямая
,
тогда прямая
![]() называется вертикальной асимптотой
графика
называется вертикальной асимптотой
графика
№6. Односторонние пределы. Классификация точек разрыва.
![]() :
Число
:
Число
![]() называется односторонним пределом
слева, если
называется односторонним пределом
слева, если
![]() ,
,
![]() ,
т.ч.
,
т.ч.
![]() ,
,
![]() :
:
![]()
![]() :
Число
:
Число
![]() называется односторонним пределом
справа, если
называется односторонним пределом
справа, если
![]() ,
,
![]() ,
т.ч.
,
т.ч.
![]() ,
,
![]() :
:
![]()
