щпоры по вм1 на первый семестр

1. Предел функции в точке. Единственность предела. Ограниченность функции, имеющей предел. Связь функции, имеющей предел, и бесконечно малой функции.

Число А называется пределом функции f в точке а, если она определена на некоторой окрестности а, т.е. на некотором интервале (c,d), где c<a<d, за исключением, быть может, самой точки а, и если для всякого >0 можно указать зависящее от него >0 такое, что для всех x, для которых имеет место неравенство . Тот факт, что А есть предел f в точке a, принято записывать или .

Теорема. Если , где A – конечное число, то на некоторой окрестности U(a) функция f(x) ограничена, т.е. существует положительное число М такое, что для всех,.

Доказательство. Из условия теоремы следует существование окрестности U(a), такой, что 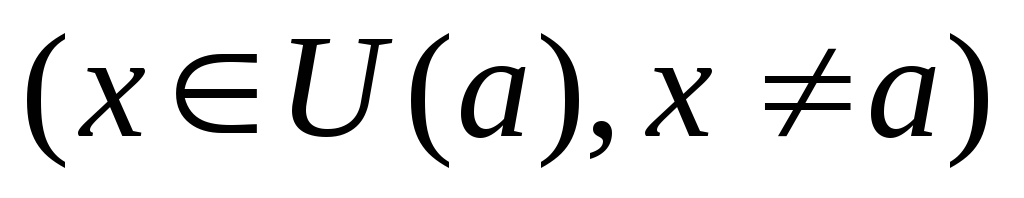. Отсюда для указанных х, где надо считать . Теорема доказана.

Функция f, для которой , называется бесконечно малой при .

2. Свойства бесконечно малых функций. Предел суммы, произведения и частного. Переход к пределу в неравенствах, предел промежуточной функции.

Функция называется бесконечно малой в точке x₀, если предел ёё в этой точке равен нолю. Функция называется бесконечно большой в точке x₀, если её предел в этой точке равен бесконечности.

Св-ва б.м.ф.:

1) Если функция f(x) ограничена, а m(x) бесконечно большая, то

2) Если абсолютная величина f(x) ограничена снизу положительным числом, а m(x) не равная нулю бесконечно мала, то

Предел суммы равен сумме пределов, предел произведения равен произведению пределов, предел частного равен частному пределов в том случае, если предел знаменателя не равен нулю.

Теорема. Если , и на некоторой окрестности U(a), ,, то . Доказательство. Пусть , ; тогда для достаточно большого n₀ имеет место неравенство и после перехода к пределу неравенство .

Теорема .Если

, (1)

и на некоторой окрестности U(a), , 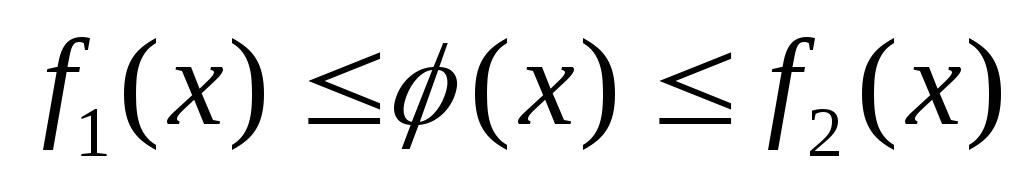то

. (2)

Доказательство. Пусть , ; тогда при достаточно большом n₀ для и в силу (1) существует предел , равный А, а так как {x_n} есть произвольная сходящаяся к а последовательность, то имеет место (2).

3. Непрерывность функции в точке. Свойства непрерывных функций. Асимптотическое разложение непрерывной функции.

Функция f(x) называется непрерывной в точке х₀, если она определена в некоторой окрестности этой точки, в том числе в самой точке х₀, и если её приращение в этой точке, соответствующее приращению аргумента , стремится к нулю при : .

КОРОЧЕ: .

Св-ва непрерывных ф-ций:

1. Если ф-ция y=f(x) непрерывна на [a,b] и f(a)*f(b)<0, т.е. знаки f(a) и f(b) противоположны, то на (a,b) найдется хотя бы одна точка х=с, что f(c)=0 (график)-теорема Больцана-Коши.

2. Если ф-ция y=f(x) непрерывна на [a,b], то она ограничена на этом промежутке.

3. Если ф-ция y=f(x) непрерывна на [a,b], то она достигает на этом отрезке min m и max M (теорема Вейерштрасса).

в точке:

1. если ф-ция f(x) и g(x) непрерывна в х₀, то их сумма, произведение, частное (при (х₀)0) явл-ся ф-циями, непрерывными в х₀

2. если ф-ция y=f(x) непрерывна в х₀, и f(x₀)>0, то существует окрестность х₀, в которой f(x)>0

3. если y=f(U) непрерывна в U₀, а U=(x) непрерывна в U₀=(x₀), то сложная ф-ция y=f[(x)] непрерывна в х₀.

4. Эквивалентные б.м.ф. Таблица эквивалентных б.м. функций. Замена отношения бесконечно малых эквивалентными при вычислении пределов.

Эквивалентными (асимптотически равными) называют функции (x) и (x) (обе стремящиеся к нулю), если выполняется свойство .

Если b(x) и c(x) – эквивалентные б.м.ф. при , тогда .

5. Сравнение б.м.ф. Б.б.ф., связь с б.м.ф. Вертикальная асимптота графика функции.

Если функции (x )и (x), участвующие в 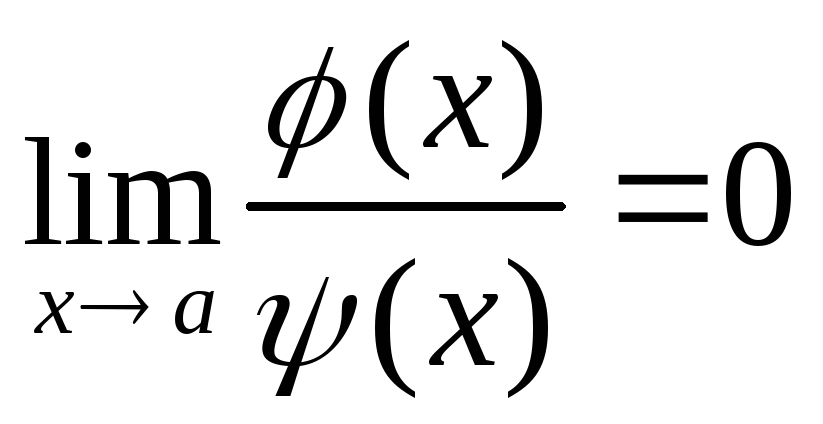, суть бесконечно малые при , то (x) при есть бесконечно малая высшего порядка по отношению к (бесконечно малой) (x) (если же это были бесконечно большие, то (x) более низкого порядка, чем (x).

Теорема о связи ббф и бмф. Пусть функция f(x)-бб при . Тогда функция a(x) –бм при

Доказательство (?). .

Прямая х=а называется вертикальной асимптотой графика функции y=f(x), если хотя бы одно из предельных значений ; равно + или –.

6. Односторонние пределы. Классификация точек разрыва.

Число А называется пределом функции f(x) в точке x=a справа (при +0), если.

Точки, в которых функция f(x) не является непрерывной, называются точками разрыва для функции f(x). Если в точке x=a существуют пределы f(a+0), f(a–0), но неравенство не выполняется,то точка х=а называется точкой разрыва первого рода для функции f(x). Причём, если , то точка x=a называется точкой устранимого разрыва для функции f(x). Если же в точке x=a у функции f(x) не существует правого или левого предела или же эти пределы бесконечны, то функция f(x) имеет в точке x=a разрыв второго рода.

7. Предел функции в бесконечности. Наклонная асимптота графика функции. Горизонтальная асимптота график функции.

Число А называется пределом функции f(x) при , если для произвольного числа найдётся число N>0 (зависящее от ) такой, что для всех значений x, удовлетворяющих неравенству, будет иметь место неравенство .

Прямая Y=kx+b называется наклонной асимптотой графика функции y=f(x) при , если функция f(x) представлена в виде , где (x)=o(1) (). Если коэффициент k=0 т.е. уравнение наклонной асимптоты имеет вид Y=b, то тогда её называют горизонтальной асимптотой. НО для того, чтобы график функции y=f(x) имел при наклонную асимптоту, необходимо и достаточно, чтобы существовали два предельных значения и .

8. Производная. Геометрический и механический смысл производной. Уравнение касательной и нормали к графику функции.

Производной функции f(x) в точке x называется предел её приращения в этой точке к соответствующему приращению аргумент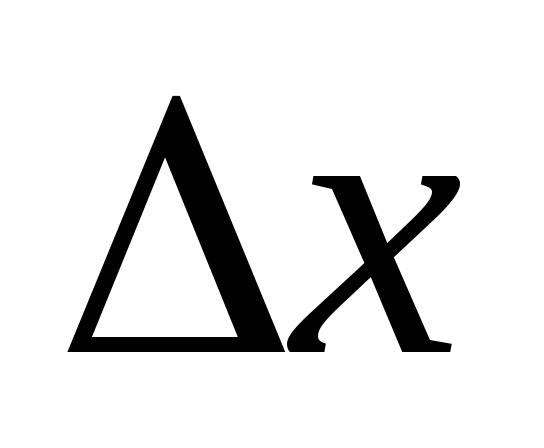а, когда стремиться к нулю (при условии, что этот предел существует). Для обозначения производной используют символы Определение записывается и таким образом .

Геометрический смысл производной заключается в том, что есть tg угла наклона касательной, проведенной в точке x₀. KN=y, MK=x

tg угла KMN=y/x

вычислим предел левой и правой части:

limtg=lim(y/x) x0

tg₀=y`

₀

При x0 секущая MNзанять положение касательной в точке M(tg₀=y`, ₀).

Касательной Т к кривой y=f(x), проходящей через точку (x;f(x)), называется предельное положение секущей при x0. Уравнение касательной в точке M(x₀,f(x₀)) записывается в виде .

Нормалью к графику функции в точке M(x₀,f(x₀)) назовём прямую, проходящую через точку М и перпендикулярную касательной, проходящей через эту же точку.

9. Дифференцируемость функции. Дифференциал. Необходимое и достаточное условие дифференцируемости. Геометрический смысл дифференциала. Таблица производных.

Функция f(x) называется дифференцируемой в точке х, если её приращение в этой точке может быть представлено в виде , где величина А не зависит от x.

Теорема. Для того, чтобы функция f(x) была дифференцируемой в точке х, необходимо и достаточно, чтобы она имела в этой точке конечную производную. Тогда величина А из равна производной: A=f’(x).

Достаточность. Из существования производной выводим дифференцируемость

Необходимость. Из дифференцируемости функции выводим существование производной .

Дифференциалом функции называют главную часть приращения в точке х, соответствующим приращению аргумента х. Дифференциал dy=Ax=f’(x)x или dy=f’(x)dx.

Геометрический смысл: дифференциал - изменение ординаты касательной, проведенной к графику ф-ции в точке (x₀,f(x₀)) при изменении x₀ на величину x

Св-ва: 1. (UV)`=U`V`, то (UV)`dx=U`dxV`dx, d(UV)=d(UV)

2. (UV)`=U`V+V`U, то (UV)`dx=V`dU+U`dV

3.d(c)=c`dx=0*dx=0

4. d(U/V)`=(V`dU-U`dV)/V².

10. Непрерывность дифференцируемой функции. Производные суммы, произведения и частного. Производная сложной функции. Логарифмическая производная.

Теорема. Если функция f(x) дифференцируема в точке х, то f(x) непрерывна в точке x. Доказательство. Пусть функция f(x) дифференцируема в точке x, т.е. y=Ax+o(x) (x0). Тогда , т.е. функция f(x) непрерывна в точке x.

Если z=z(x) – дифференцируемая функция от x, то формулы имеют вид:

11. Производная обратной функции. Производные обратных тригонометрических функций.

y=f(x), то x=(y) - обратная ф-ция.

Для дифференцируемой ф-ции с производной, не = 0, производная обратной ф-ции = обратной величине производной данной ф-ции, т.е. x_y`=1/y<sub>x</sub>`.

y/x=1/(x/y) - возьмем предел от левой и правой части, учитывая, что предел частного = частному пределов:

lim(y/x)=1/(lim(x/y), т.е. y_x`=1/x<sub>y</sub> или f`(x)=1/`(f(x))

Основные формулы:

Для сложных функций:

12. Производные и дифференциалы высших порядков.

y=f(x)

y``=(y`)`=lim((f`(x+x)-f`(x))/x)

x0

y```=(y``)`= lim((f``(x+x)-f``(x))/x)

f⁽ⁿ⁾(x)=[f^(n-1)(x)]`

dsinx=cosxdx

ddsinx=dcosxdx=-sinxdxdx

d²sinx=-sinxdx²

13. Функции, непрерывные на отрезке. Свойства функций, непрерывных на отрезке.

Функция непрерывна на отрезке, если она непрерывна в каждой точке этого отрезка.

1. Если ф-ция y=f(x) непрерывна на [a,b] и f(a)*f(b)<0, т.е. знаки f(a) и f(b) противоположны, то на (a,b) найдется хотя бы одна точка х=с, что f(c)=0 (график)-теорема Больцана-Коши.

2. Если ф-ция y=f(x) непрерывна на [a,b], то она ограничена на этом промежутке.

3. Если ф-ция y=f(x) непрерывна на [a,b], то она достигает на этом отрезке min m и max M (теорема Вейерштрасса).

в точке:

1. если ф-ция f(x) и g(x) непрерывна в х₀, то их сумма, произведение, частное (при (х₀)0) явл-ся ф-циями, непрерывными в х₀

2. если ф-ция y=f(x) непрерывна в х₀, и f(x₀)>0, то существует окрестность х₀, в которой f(x)>0

3. если y=f(U) непрерывна в U₀, а U=(x) непрерывна в U₀=(x₀), то сложная ф-ция y=f[(x)] непрерывна в х₀.

14. Основные теоремы дифференциального исчисления (Ролля, Лагранжа, Коши), их геометрический смысл.

Теорема Ролля.

Если функция f(x) непрерывна на заданном промеж/ [a,b] деффер. на интервале (a,b) f(a)=f(b) то существует т. с из интерв. (a,b), такая, что f’(c)=0.

Теорема Лагранжа.

Если функция f(x) непрерывна на [a,b] и дифференцирована на (a,b), то сущест.

т. с(a,b), такая, что: f(b)-f(a)=f’(c)(b-a).

Доказательство: применим т. Коши, взяв только g(x)=x, тогда g’(x)=10.

Теорема Коши.

Если f(x), g(x) удовл. трем условиям:

1). f(x), g(x) непрерыв. на промеж [a,b]

2). f(x), g(x) деффер. на интервале (a,b)

3). g’(x)0 на интер. (a,b), то сущ. т. с

g(b)g(a) (неравны по теореме Ролля).

1). F(x) – непрерывна на [a,b]

2). F(x) – деффиренцирована на (a,b)

3). F(a)=0 ; F(b)=0

по теореме Ролля сущ. с(a,b); F’(с)=0

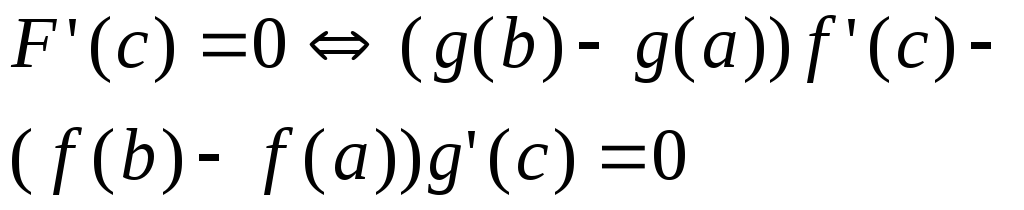
15. Правило Лопиталя для вычисления пределов.

Пусть функции f(x) и g(x) определены и дифференцируемы в некоторой проколотой окрестности точки а. Пусть и в указанной окрестности. Тогда, если существует , то существует и имеет место равенство =.

Доказательство. Доопределим функции f(x) и g(x) при х=а: f(a)=0, g(a)=0. Тогда эти функции станут непрерывными в окрестности точки а.

Рассмотрим отрезок [а;х], если x>a и отрезок [x;a], если x<a, причём х принадлежит окрестности, о которой говориться в условии теоремы.

Для функций f(x) и g(x) на указанных отрезках выполнены условия теоремы Коши. Поэтому можно записать причём . Поэтому, если , то и . Так как по условию теоремы существует , то существует и и эти пределы равны. Стало быть ==.

16. Условие возрастания и убывания дифференцируемой функции на интервале.

Функция f(x) называется неубывающей на интервале (a;b), если для произвольных , удовлетворяющих условию x_1<x₂ справедливо неравенство . Аналогично определяется невозрастающая функция.

Теорема. Для того, чтобы дифференцируемая на интервале (a;b) функция f(x) не убывала на этом интервале, необходимо и достаточно, чтобы производная f’(x) была неотрицательной на этом интервале.

Доказательство. Необходимость. Пусть функция f(x) не убывает на (a;b), т.е. для любых , удовлетворяющих условию x_1<x₂ следует неравенство . Пусть х – любая точка интервала (a;b), дадим аргументу положительное приращение Δх, не выводящее его из интервала (a;b). Тогда , т.к. . Поэтому .

Достаточность. Требуется доказать, что из условия на (a;b) следует, что для любых , удовлетворяющих условию . Применим теорему Лагранжа , т.к. и

17. Экстремумы функции. Необходимые условия экстремума. Достаточные условия экстремума до первой производной.

Точка х называется точкой необходимый признак экстрем

max ф-ции, если значение мума: ф-ия а(x) может иметь

ф-ции в этой точке max и min только в тех точках

- наименьшее в некоторой в которых f’(x)=0 или не сущ.

ее окрестности.

1- локальный max

2- локальный min

3- глобальный max

4- глобальный min

если tg>0, то f`(x)>0

если tg<0, то f`(x)<0

(В них можно построить  касательных).

Достаточный признак: точка х₀ является точкой экстремума, если ее производная в этой точке меняет знак:

- если с “+” на “-”, то х₀- т. max

- если с “-” на “+”, то х₀- т. min

18. Формула Тейлора с остаточным членом в форме Пеано.

Теорема. Пусть функция f(x) имеет в некоторой окрестности точки а производную порядка n+1. Пусть x – любое значение аргумента из этой окрестности. Тогда между точками a и x найдётся точка , что справедлива формула где

19. Представление функций e^x, sinx, cosx, ln(1+x), (1+x)^ по формуле Тейлора. Применение формулы Тейлора для приближённых вычислений.

(1+х)ª =1+ах+(а(а-1)х²)/2+(а(а-1)(а-2)х³)/6+…+(а(а-1)…(а-n-2)* *хⁿ‾¹)/((n+1)!)+o(xⁿ‾¹)

Вычислим с точностью 10^-3. Воспользуемся разложением 5 при =1/3

ФОРМУЛА – 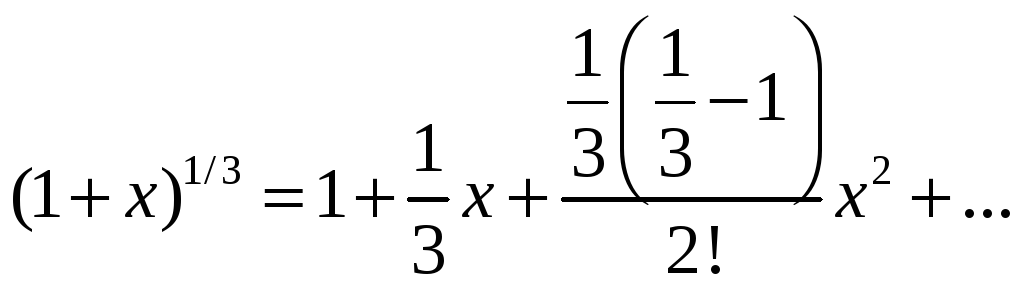преобразуем сначала .

Применим ФОРМУЛУ, ограничась тремя членами ;

, здесь 0<<1. Таким образом с точностью 10^-3

20. Направление выпуклости. Точки перегиба. Необходимое и достаточное условия. Исследование по высшей производной.

Линия называется выпуклой, если она пересекается с любой своей секущей не более чем в 2х точках. Линия называется вогнутой, если она целиком лежит по 1 сторону от касательной, проведенной в любой ее точке.

Точка перегиба - точка, отделяющая выпуклый участок дуги от вогнутого.

Необходимый признак выпуклости и вогнутости: если линия на интервале выпуклая, то ее 2я производная <=0; если линия на интервале вогнутая, то ее f``(x)>=0

Достаточный признак: если f``(x) всюду в интервале “-”, то линия в интервале выпуклая; если f``(x)>0, то линия вогнутая.

Признаки точки перегиба: чтобы X₀ была т. перегиба, <=> чтобы у`` в этой точке = 0 и меняла знак при переходе х через х₀.

21. Исследование на экстремум с помощью производных высших порядков. Достаточное условие экстремума по второй производной.

Короче – если чётная производная (перед ней все нулевые), тогда как х², а если нечётная производная (перед ней все нулевые), то как х³.

Теорема. Пусть функция f(x) имеет в стационарной точке x=c вторую производную. Тогда функция f(x) имеет в точке x=c локальный максимум, если f”(c)<0 и локальный минимум, если f”(c)>0.

Доказательство(для min). Так как f’(c)=0, то . Так как предельное значение больше нуля, то , при достаточно малых , т.е. для (справа от точки с), а для (слева от с) . Получается (ну!..), чо точка x=c – точка локального минимума.

22. параметрически заданные функции. Производная функции заданной параметрически. Касательная к кривой,заданной параметрически.

Пусть функции x = φ (t) и y = ψ(t) определены на некотором отрезке [α, β]. Переменную t будем называть параметром.

Если x = φ (t) взаимно однозначна на отрезке [α, β], то она имеет обратную функцию t(x) = φ ^{− 1} (x). Подставляя ее в равенство y = ψ(t), видим, что переменная y является сложной функцией переменной x:

В этом случае говорят, что функция y = f(x) задана параметрически уравнениями

x = φ (t) (1)

y = ψ(t)

где t[a,b]

Производная первого порядка функции, заданной параметрически

Теорема 1. Пусть функция y = f(x) задана параметрически уравнениями (1), причем функции φ (t) и ψ(t) дифференцируемы в некоторой точке t₀ О (α, β), и φ '(t₀) ≠ 0.

Тогда функция y = f(x) дифференцируема в точке x₀ = φ(t₀), причем

f’(xo)= ψ’(t)

φ’(t) t=to

Доказательство.

В условиях теоремы функция j(t) имеет дифференцируемую обратную функцию t(x) = j ^{− 1} (x), производная которой в точке x₀ = j(t₀) определяется формулой

t’(x)= 1/ φ’(t(x)) 

Дифференцируя f(x) = ψ(t(x)) в точке x₀ = j(t₀) как сложную функцию x, при t = t₀ получаем

f’(Xo)= ψ’(t)*t’(x)= ψ’(t)

φ’(t) t=to

Касательная и нормаль к плоской кривой.

   Пусть даны кривая y = f(x) и точка M (x₁ ; y₁) на ней. Требуется составить уравнения касательной.    Как известно, угловой коэффициент k касательной к кривой y = f(x) в точке M (x₁ ; y₁) равен значению f '(x₁) производной y' = f '(x) при x = x₁/ Следовательно, уравнение касательной можно записать в виде уравнения прямой, проходящей через данную точку в данном направлении, т.е. в виде

y - y₁ = f '(x₁)(x - x₁)