2. Дивергенция (расхождение) некоторого вектора e в данной точке пространства – это, фактически, поток этого вектора из бесконечно малого объема dV, находящегося в этой точке пространства:

div E = (24)

Понятно, что поверхность S, ограничивающая объем dV (V 0), является замкнутой поверхностью, поэтому и интеграл в (24) взят по замкнутой поверхности. Дивергенция – скалярная величина, которая, в общем случае, различна для разных точек пространства. Дивергенция образует скалярное поле в данном векторном поле.

Приведем без доказательства теорему Гаусса-Остроградского: поток вектора Е через замкнутую поверхность S равняется интегралу от divЕ по объему V, ограниченному поверхностью S: = . (25)

Обратите внимание, левый интеграл берется по замкнутой поверхности (двойной интеграл), а интеграл справа - по объему (тройной интеграл).

Приведем выражение для дивергенции вектора Е через проекции этого вектора без вывода. Пусть дан вектор E = E_x i + E_y j + E_z k, тогда дивергенция этого вектора в данной точке пространства P(x₀, y₀, z₀) определяется выражением:

div E = + + , (26)

где частные производные берутся в рассматриваемой точке P(x₀, y₀, z₀).

Задача 4. Определить дивергенцию радиус-вектора r = x i + y j + z k и поток этого вектора через произвольную замкнутую поверхность, ограничивающую объем пространства V.

Решение. Их определения дивергенции (26) имеем:

div r = + + = 1 + 1 + 1 = 3.

По теореме Гаусса-Остроградского (25) поток вектора r через замкнутую поверхность S равен

= = = 3V.

В частности, поток через всю полную поверхность цилиндра равен = 3V = 3R²h, где V = R²h – объем цилиндра, R – радиус основания цилиндра, h – высота цилиндра (см. предыдущую задачу).

1.3.7. Криволинейный интеграл, циркуляция вектора, ротор (вихрь) вектора

1. Пусть дано векторное поле b(x, y, z). На рис.10 показаны силовые линии и вектор b в точке M(x, y, z) этого векторного поля. Проведем в векторном поле через точку M некоторую дугу L (дуга может и не совпадать с силовой линией). Направление выбранного перемещения по дуге (здесь из точки M в точку N) определим вектором dl. Модуль dl этого вектора является дифференциалом дуги. Из векторов b и dl можно образовать скалярное произведение: (bdl).

Физический смысл этого скалярного произведения в различных векторных полях, разумеется, различен. Например, если в качестве вектора b будет вектор силы F, то скалярное произведение (Fdl) есть элементарная работа силы F на перемещении dl. Если же векторным полем является индукция магнитного поля В, то глубокое физическое содержание приобретает не само по себе скалярного произведения (Вdl), а интеграл этого произведения по замкнутой кривой (по замкнутому контуру).

Интеграл по дуге L от точки M до точки N :

= = (27)

называется криволинейным интегралом, где  - угол между векторами b и dl, b_l – проекция b на направление вектора dl. Заметим, криволинейный интеграл всегда можно свести к обыкновенному интегралу. Интеграл (27) можно также представить через проекции векторов b и dl: т.к. b = b_x i + b_y j + b_z k и dl = x i + y j + z k , то

= . (28)

2. Циркуляция вектора. Криволинейный интеграл , взятый по замкнутому контуру L, называется циркуляцией вектора b. Примеры: а) циркуляция вектора напряженности Е электростатического поля равна нулю: - работа электростатического поля на замкнутой кривой равна нулю; б) циркуляция индукции магнитного поля определяется электрическим током I, который охватывается контуром L: = . В примере (б) знак тока I_k зависит от направления обхода контура L: если направление обхода L и направление тока I_k связаны правилом правого винта, то ток I_k положителен. Например, в ситуации, показанной на рисунке 11, токи I₁ и I₃ - положительные, ток I₂ – отрицательный, ток I₄ не вносит вклада в циркуляцию.

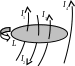
Рис. 11.

Введем понятие циркуляции на примере циркуляции вектора индукции B магнитного поля, созданного током I, текущим по бесконечно длинному проводу.

Напомним, интегрирование закона Био-Савара-Лапласа в случае прямого тока приводит к тому, что модуль магнитной индукции определяется формулой B = , где b - расстояние от провода до рассматриваемой точки поля.

Определим циркуляцию B, представив этот вектор через его компоненты в декартовой системе координат.

На рис. 12 ось 0z совмещена с проводом. Направление вектора индукции B определяется правилом правого винта. Силовые линии лежат в плоскости, перпендикулярной оси 0z, поэтому проекция вектора B на эту ось B_z = 0. Можно показать, что две остальные компоненты - B_x и B_y - имеют вид:

B_x = и B_y = .

Вывод этих выражений несложен, но довольно громоздок, и здесь не приводится. Итак, вектор магнитной индукции, выраженный через компоненты, имеет вид:

B = . (29)

Попутно заметим: т.к. B = , то

B = B= = = = ,

что соответствует приведенному выше выражению для модуля индукции.

Рис. 12.

Определим циркуляцию В по плоскому контуру L. Пусть контур представляет собой окружность с центром на проводе с током и лежит в плоскости, перпендикулярный проводу с током. В этом случае расстояние b от провода до точек контура везде одинаковый и равен радиусу контура b. Циркуляция магнитной индукции (29) с учетом (28) по такому контуру примет простой вид:

= = , где

dl - бесконечно малый элемент контура (dl = dx i + dy j). Интеграл равен удвоенной площади круга радиуса b, т.е. 2S = 2b² . Таким образом,

= = ₀I . (30)

Заметим, циркуляции магнитной индукции имеет вид (30) при любой форме контура L.

Сила тока I = скалярная величина, определяемая зарядом, протекающим за единицу времени через поперечное сечение проводника. Выразим (30) с использованием векторной характеристики электрического тока – плотности тока j. Направление вектора j совпадает с направлением движения положительных зарядов. Модуль вектора j численно равен отношению силы тока dI к поперечной площадке dS_, через которую протекает электрический ток: j = . Если площадка dS ориентирована произвольным образом к вектору j (ориентация площадки dS характеризуется вектором нормали n, т.е. введением вектора площади dS = dSn, см. рис. 13), то dI определяется скалярным произведением

dI = jdS = j dS cos = j dS_ = j dS_j .

Здесь  - угол между векторами j и dS, а dS_ = dS_j - проекция вектора dS на направление вектора j. В частности, если j  dS, то ток через элементарную площадку dS равен нулю. Электрический ток I через конечную площадку S определится интегралом: I = . Таким образом, циркуляцию (30) можно представить в форме:

= ₀ = ₀ , (31)

где S – поверхность, натянутая на контур L. Циркуляцию (31) можно записать и в форме:

= ₀ = ₀ , (32)

где j_n = j cos - проекция вектора j на направление нормали n (или, что то же самое, на направление вектора S, см. рис. 14).

Формулы (30), (31) и (32) верны для контура любой формы и любой ориентации площадки S, лишь бы контур охватывал проводник с током. Если ток охватывается контуром L, то поверхность S, натянутая на контур, пронизывается вектором j. Согласно (31), циркуляция вектора В при данной площади S достигает максимума, когда jdS. Итак, циркуляция зависит от размеров площадки и от ориентации площадки относительно вектора j. В частности, если вектор j лежит на площадке S, натянутая на контур L (т.е. вектор j не пронизывает площадку S), то циркуляция вектора В по такому контуру L равна нулю.

Рис. 13. Рис. 14.

В соответствии с (31) и (32) циркуляция вектора В определяется другим вектором (если, разумеется, циркуляция существует!). В нашем примере – это вектор j. Точнее: циркуляция вектора определяется проекцией другого вектора на нормаль к плоскости контура, вдоль которой берется циркуляция (формула (32)).

3. Ротор (вихрь) вектора. Понятие ротора вектора введем из обобщения приведенных выше рассуждений. Допустим, что циркуляция произвольного вектора b по малому контуру L не равна нулю (  0). Натянем на контур L поверхность S. Тогда поверхность S будет пронизываться еще одним вектором, определяющим эту циркуляции. Этот вектор называется ротором векторного поля b, который обозначается как rotb. Проекция ротора вектора на нормаль к площадке S в данной точке P(x, y, z) векторного поля b определяется пределом отношения циркуляции вектора b по контуру L к величине площадки S при стягивании площадки к точке P(x, y, z) (рис.15):

= rot_nb (33)

Вектор rotb проходит через точку P и перпендикулярен S_ = S_j. Подчеркнем, в определении (33) rot_nb – это проекция вектора rotb на направление нормали n в данной точке векторного поля, а не сам вектор rotb.

Циркуляция при неизменной площади S зависит от ориентации вектора S относительно направления вектора rotb. Циркуляция достигает максимального значения для площадки, перпендикулярной к rotb (т.е. при S rotb или, n rotb). При n rotb модуль ротора равен модулю проекции ротора на нормаль к поверхности S: rotb= rot_nb

В ектор b в разных точках P(x, y, z) в общем случае различен. Если вычислить rotb во всех точках векторного поля b, получаем новое векторное поле - поле вектора rotb.

Рис. 15.