1.3.5. Уравнение векторной (силовой) линии

Векторная линия – это линия, касательные к которой в каждой ее точке совпадают с направлением векторного поля в этих точках. Пусть дано поле вектора b. Значение этого вектора в общем случае разное для разных точек пространства, т.е. b является функцией радиус-вектора (координат) точек пространства: b(r) или b(x,y,z). Через компоненты вектор b имеет вид:

b(x,y,z) = b_x i + b_y j + b_z k.

На рисунке 8 показана одна силовая линия некоторого векторного поля b(x,y,z). Вектор b(x,y,z) является касательной к силовой линии. Касательной к силовой линии является также и дифференциал радиус-вектора dr = dx i + dy j + dz k. Таким образом, вектора b и dr коллинеарны. В соответствии с формулой (7) для коллинеарных векторов имеем:

. (21)

У равнение (21) является дифференциальным уравнением векторной линии.

Рис.8. К введению понятия уравнения векторной линии

Задача 2. Определить уравнение векторной линии (уравнение силовых линий) поля E = k (здесь Е, например, напряженность электростатического поля точечного электрического заряда, находящегося на точечном или шарообразном теле, или напряженность гравитационного поля однородного шара).

Решение.

Напомним, силовые линии электростатического поля практически точечного заряженного тела представляют собой прямые линии, которые начинаются (или заканчиваются) на заряде. Покажем это, используя уравнение (21).

П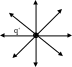 оместим точечный заряд в начало координат. Т.к. dr = dx i + dy j + dz k и E = k , где компоненты вектора E соответственно равны E_x = , E_y = , E_z = . Дифференциальное уравнение силовой линии, в соответствии с (21), примет вид: (здесь общий множитель отброшен). После интегрирования этого уравнения, получим: lgx = lgy + lgC₁; lgy = lgz + lgC₂; lgx = lgz + lgC₃ или

x = C₁ y; y = C₂ z ; x = C₃ z , (*)

где С₁, С₂, С₃ – произвольные константы, причем С₃ = С₁ С₂. Все три уравнения (*) являются уравнениями прямых, проходящих через начало координат. Запишем уравнение прямой в пространстве в каноническом виде. Т.к. x = C₁ y = C₃ z и С₃ = С₁ С₂ , то каноническое уравнение примет вид: , где x₀ = y₀ = z₀ = 0. Силовые линии положительного заряда q⁺ показаны на рисунке к данной задаче:

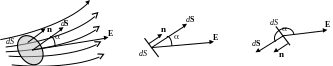1.3.6. Поток вектора через поверхность и дивергенция вектора

1. Понятие потока вектора через поверхность рассмотрим на примере потока напряженности электрического поля.

«а» «б» «в»

Рис. 9. К введению понятия потока вектора

На рис.9-а показаны силовые линии вектора напряженности Е электрического поля и элементарная поверхность dS, которая пронизывается силовыми линиями. Рис. 9-б дублирует рис. 9-а, где для исключения загромождения чертежа силовые линии не показаны, а поверхность dS представлена ее следом. Вектор Е направлен по касательной к силовой линии и пронизывает мысленную элементарную поверхность dS. Вследствие элементарности поверхности dS (dS – бесконечно малая поверхность) везде на поверхности dS напряженность электрического поля Е можно считать постоянным вектором.

Ясно, что в зависимости от расположения площадки dS по отношению к силовым линиям, эти силовые линии или пронизывают площадку dS, или скользят по площадке. Другими словами, в зависимости от ориентации площадки dS по отношению к вектору Е наблюдается или некоторый поток вектора Е через площадку dS , или поток Е через dS отсутствует (равен нулю).

Взаимную ориентацию вектора напряженности Е и элементарной поверхности dS удобно осуществлять с использованием вектора поверхности dS, а поток Е через площадку dS – скалярным произведением векторов Е и dS.

Вектор dS определяется выражением: dS = dS n, где n – единичный вектор, перпендикулярный к поверхности dS. Ориентация вектора Е по отношению к поверхности dS определяется углом  между векторами Е и dS. Тогда элементарный поток вектора Е через поверхность dS выражается скалярным произведением этих векторов:

dФ = EdS = Еn dS =E dS cos = Е_n dS, (22)

где угол  - угол между вектором Е и вектором n (или dS), Е_n = E cos - проекция вектора Е на нормаль к поверхности n (или на вектор dS).

Максимальный поток будет при cos = 1, т.е. при  = 0^о. Если cos = 0, т.е. если  = 90^о, то поток вектора Е через поверхность dS будет отсутствовать (поток равен нулю), т.к. при  = 90^о вектор Е скользит по поверхности dS, не пронизывает эту поверхность.

При других углах  имеем промежуточные значения потока. Т.к. cos принимает значения от (+1) до (1), то поток может быть и положительным (рис. 9-а или 9-б) и отрицательным (рис. 9-б).

Если поверхность конечна и равна S, то поток вектора Е через поверхность S будет определяться суммированием всех элементарных потоков на этой поверхности, т.е. поверхностным интегралом:

Ф = = = , (23)

Мысленная поверхность, через которую имеется поток вектора, может быть и замкнутой (замкнутая поверхность – это поверхность без краев; например: поверхность шара, призмы, поверхность булыжника и т.п.). Замкнутая поверхность S ограничивает некоторый объем V. За направление вектора dS, т.е. за направление вектора n, обычно берут направление внешней нормали к каждой точке замкнутой поверхности. Поток определяется интегралом по этой замкнутой поверхности: Ф = . Разумеется, источник векторного поля может находиться как внутри замкнутой поверхности, так и вне этой замкнутой поверхности. В нашем примере источником вектора Е может быть, например, точечный электрический заряд q, который может находиться как внутри, так и вне мысленной замкнутой поверхности. Поток вектора – это скаляр и образуется скалярным произведением.

Поток вектора через замкнутую поверхность можно условно представить как разность между числом входящих и числом выходящих силовых линий. В частности, если число входящих и выходящих силовых линий одинаково, то поток через замкнутую поверхность равен нулю.

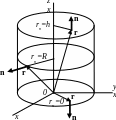
Задача 3. Найти поток радиус-вектора r материальной точки через прямой цилиндр. Начало координат лежит в центре нижнего основания, радиус основания R, высота цилиндра h (см. рисунок к задаче).

Решение. На рисунке векторами n обозначены единичные вектора к основаниям цилиндра и боковой поверхности цилиндра (вектора n являются внешними нормалями к цилиндру). Для решения задачи воспользуемся определением потока , где r_n – проекция радиус-вектора r на направление нормали n. Поток радиус-вектора r имеет место быть через боковую поверхность и верхнее основание цилиндра. Через нижнее основание поток равен нулю, т.к. на нижнем основании угол между векторами r и n равен 90^о и проекция r_n = 0 (вектор r скользит по нижнему основанию и не пересекает поверхность). Проекция вектора r на направление вектора n на боковую поверхность равна r_n = R, проекция вектора r на направление вектора n на верхнем основании цилиндра равна r_n = h. Поток вектора r будет определяться суммой потоков через боковую поверхность, верхнее основание и нижнее основания цилиндра, т.е. выражением:

= + + .

Рассчитаем каждый из интегралов:

= = R S = R 2Rh = 2R² h , = = h R², =0.

Итак, поток вектора r равен: = 2R² h + h R² = 3 h R².