Глава 1. Математический аппарат теории поля

1. Элементы векторной алгебры (скалярные и векторные величины,

операции с этими величинами).

1. Скалярные и векторные величины.

Физические величины, с которым имеют дело в теории физических полей, подразделяются на скаляры и векторы. Скалярная величина (скаляр) характеризуется одним числом при выбранной единице измерения. Примерами скалярных величин являются температура, масса, энергия. Скаляром является также отвлеченное число. Две однородные скалярные величины равны, если равны их численные значения.

Векторная величина (вектор) характеризуется численным значением и направлением в пространстве. Примерами векторных величин являются скорость, импульс, плотность электрического тока, индукция магнитного поля. Численное значение векторной величины имеет ту или иную единицу измерения. Например, единицей численного значения скорости в системе единиц СИ является 1 м/с. Численное значение вектора называется модулем, величиной или длиной вектора. В дальнейшем векторные величины будем обозначать полужирным шрифтом: v, p, E. Скалярные величины будем обозначать курсивом. Примерами такого обозначения являются модули векторов:v= v, p= p, E= E. Математическое представление некоторого выделенного направления в пространстве (можно назвать это направление - положительным направлением) осуществляется безразмерным отвлеченным единичным вектором. Примерами таких векторов являются единичные орты i, j, k, порождающие декартовую систему координат (рис.1). Орты i, j, k взаимно ортогональны, а их модули равны единице:i= i = 1,j= j =1,k= k =1. Другой пример. С помощью единичного вектора (обозначим этот вектор, например, через n) можно ввести понятие ориентированной поверхности. Для этого единичный вектор n устанавливается перпендикулярно элементарной поверхности площадью dS. По направлению вектора n можно судить об ориентации поверхности в пространстве и, соответственно, ввести вектор элементарной площади dS = dS n (рис.1).

Два однородных вектора a и b равны между собой (a = b), если они одинаково направлены и равны по модулю. На рисунках вектор обозначается направленным отрезком (стрелкой). Равные однородные вектора представляются в виде двух равных по длине параллельных (совмещенных) стрелок, направленных в одну сторону.

О тносительно некоторой декартовой системы координат вектор a представляется через компоненты а(a_x, a_y, a_z): a = a_x i + a_y j + a_z k. Модуль вектора а определяется через компоненты по теореме Пифагора (рис. 2):  а = а =

Рис.1.

1.2. Операции с векторными величинами

1.2.1. Вектор а, т.е. произведение вектора a на скаляр , коллинеарен вектору а, модуль которого равен а. Если  >0, то векторы а и а направлены в одну сторону, если  <0, то а и а направлены противоположно.

1.2.2. Сумма (разность) однородных векторов a и b (рис. 2) определяется правилом треугольника (или, что то же самое, правилом параллелограмма).

«а» «в»

Рис. 2. «а»: сумма векторов: c = a + b; «в»: разность векторов: c = a  b= a + (1)b

Пример. Лодка движется относительно воды со скоростью v₁ = 3 м/с перпендикулярно берегу, скорость течения реки v₂ = 4 м/с. Тогда скорость лодки относительно берега равна v = 5 м/с. Угол  между векторами v₁ и v будет определяться выражением cos  = 0,6.

1.2.3. Скалярное произведение векторов. Скалярное произведение векторов ab называется произведение модулей векторов на косинус угла между этими векторами:

ab = ab cos(a^b). (1)

Здесь угол между векторами a и b обозначен через (a^b). В результате скалярного произведения векторов получается скалярная величина. Из определения скалярного произведения непосредственно следует, что это произведение коммутативно, т.е. ab = ba.

П ример. На рисунке 3 показан пример использования скалярного произведения при определении физической величины. Элементарная работа A силы F на перемещении dl определяется как скалярное произведение силы на перемещение: A = Fdl = F dl cos, где  – угол между векторами F и dl, т.е. угол (F^dl). Если обозначить проекцию F на направление dl через F_l , тогда A = Fdl = F dl cos = F_l dl, т.к. F_l = F cos.

Рис.3. Частица массой m перемещается по траектории L, на частицу действует сила F.

Элементарная работа A силы F на элементарном перемещении dl определяется

выражением A = Fdl.

Работа силы F на конечном пути будет определяться криволинейным интегралом по траектории движения L: А = = .

Если векторы a и b взаимно перпендикулярны, то ab = 0, т.к. cos 90^о = 0. Если векторы коллинеарны (параллельны или антипараллельны), то ab =  ab, т.к. cos 0⁰ = 1, cos 180⁰ = 1. В частности aa = a² = a² .

Представим скалярное произведение через компоненты векторов в декартовой системе координат. Т.к. ii = jj = kk = 1, ij = jk = ki = 0, то

ab = (a_x i + a_y j + a_z k) (b_x i + b_y j + b_z k) = a_x b_x + a_y b_y + a_z b_z . (2)

Скалярное произведение ab не зависит от выбора координатной системы, т.е. скалярное произведение инвариантно (неизменно) по отношению ко всем декартовым системам координат. Инвариантность скалярного произведения векторов a и b в координатной форме по отношению, например, к двум произвольным декартовым системам координат К(x, y, z) и К(x ,y ,z) выражается равенством:

a_x b_x + a_y b_y + a_z b_z = a_x b_x + a_y b_y + a_z b_z. (3)

1.2.4. Векторное произведение двух векторов. Векторное произведение будем обозначать символом [a b]. В результате векторного произведения векторов a и b получается некоторый вектор c: [a b] = c. Модуль результата векторного произведения – модуль вектора с - по определению равен c = ab sin (a^b). Из этого сразу же следует, что, во-первых, векторное произведение коллинеарных векторов равно нулю:

[a b] = 0 при (ab) и (ab).

Во-вторых, модуль вектора с численно равен площади параллелограмма, построенного на векторах a и b. Направление вектора c определяется правилом правого винта: направление с = [a b] совпадает с поступательным перемещением правого винта, который поворачивают по наименьшему углу от первого вектора в векторном произведении (здесь это вектор a) ко второму, т.е. к вектору b (рис.4). Вектор c перпендикулярен плоскости, в которой лежат векторы a и b (ca и cb). Из правила правого винта следует, что

[a b] = [b a]. (4)

Векторное произведение некоммутативно и при расчетах нельзя менять местами векторы в векторном произведении.

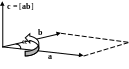
Рис. 4. Векторное произведение c = [ab]; здесь  = (a^b)

Представим векторное произведение с = [a b] через компоненты векторов в декартовой системе координат. Т.к. (см. рис.1)

[i j] = k, [j k] = i, [k i] = j, [j i] = k, [k j] = i, [i k] = j, то

[ab] = [(a_x i + a_y j + a_z k) (b_x i + b_y j + b_z k)] =

= (a_y b_z  a_z b_y)i + (a_z b_x  a_x b_z)j + (a_x b_y  a_y b_x)k. (5)

Таким образом, компоненты результата векторного произведения – компоненты вектора с - имеют вид:

c_x = [ab]_x = a_y b_z  a_z b_y,

c_y = [ab]_y = a_z b_x  a_x b_z , (6)

c_z = [ab]_z = a_x b_y  a_y b_x.

Заметим, векторное произведение [a b] можно представить в форме определителя:

[a b] = 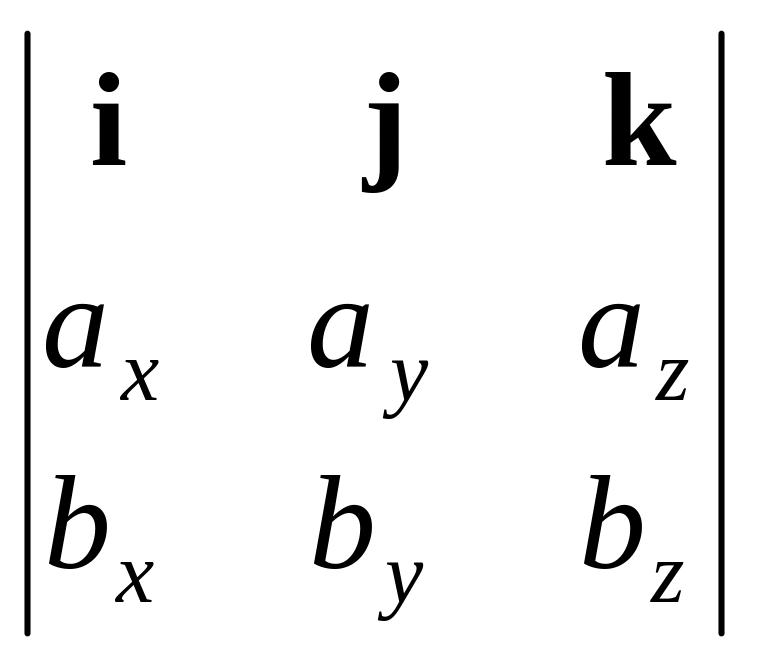. (6^*)

Для коллинеарных векторов - (ab) и (ab) - векторное произведение [a b] = 0, т.е. равны нулю все три проекции результата векторного произведения (6):

a_y b_z  a_z b_y = 0, a_z b_x  a_x b_z = 0, a_x b_y  a_y b_x = 0.

Из этих соотношений следует, что , , . Или:

, (7)

т.е. у коллинеарных векторов соответствующие проекции пропорциональны

1.2.5. Смешанное (скалярно-векторное) произведение трех векторов а[bc]. В результате такого произведения получаем скалярную величину. Т.к. смешанное произведение, в которое входит два одинаковых орта, равно нулю, т.е. равны нулю произведения вида

i[jj] = 0 , i[kk] = 0, i[ik]= 0 i[ki] = 0 и т.д., то

получим: а[bc] = a_xb_yc_z  a_xb_zc_y + a_yb_zc_x  a_yb_xc_z + a_zb_xc_y  a_zb_yc_x . (8)

Смешанное произведение допускает циклическую (стековую) перестановку векторов:

а[bc] =c[а b] = b[cа]. (9)

По своему геометрическому смыслу смешанное произведение равно объему параллелепипеда, построенного на векторах а, b и c. Действительно, скалярное произведение вектора а на вектор [bc] выражается соотношением а[bc] = a[bc]cos , где модуль векторного произведение [bc] численно равен площади параллелограмма со сторонами b и c, а высота параллелепипеда определяется отношением h = a cos (рис.5). Если все три вектора а, b и c лежат в одной плоскости (компланарные вектора), то объем параллелепипеда равен нулю, т.к. в этом случае а[bc] = 0.

Рис. 5. Геометрический смысл смешанного произведения а[bc].