Линейный коэффициент корреляции
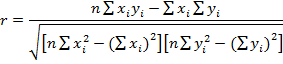
и
– индивидуальные значения факторного
и результативного признаков соответственно,
и
- средние значения факторного и
результативного признаков соответственно,
-средние квадратические отклонения
факторного и результативного признаков
соответственно,
n- число единиц наблюдения.
-1
,
чем
ближе значение по модулю к 1, тем сильнее
линейная
связь
Шкала качественной оценки количественных значений коэффициентов линейной корреляции
Значение коэффициента корреляции (по модулю) |
Качественная характеристика силы связи |
До 0,3 0,3-0,7 0,7-0,9 0,9-0,99 |
Практически отсутствует (слабая) Средняя Высокая Весьма высокая |
К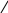
ритерий
Блэкмана:/
– возможно применение уравнения линейной
регрессии.
Наиболее частые типы регрессионных уравнений
линейная
показательная 
гиперболическая
параболическая 
степенная
логарифмическую 
логистическая
Определение
коэффициента регрессии: 
,
где
r – линейный коэффициент корреляции,
– средние квадратические отклонения
соответственно значений результативного
и факторного признаков
Средняя
квадратическая ошибка уравнения
регрессии:
,
где
,
-
фактические значения результативного
признака, полученные по данным наблюдения;
-
значения результативного признака,
рассчитанные по уравнению корреляционной
связи и полученной подстановкой значений
факторного признака
в уравнение регрессии;
m - число параметров в уравнении регрессии;
n- число единиц наблюдений.
Ошибка
аппроксимации уравнения регрессии:
*
100%
Если 
и
*
100%
10-15%, то построенное уравнение регрессии
можно рекомендовать к использованию.
Коэффициент
эластичности: 
=b
,
где
b
– коэффициент регрессии,
и 
- средние значения факторного и
результативного признака соответственно
β-коэффициент:
,
где b
– коэффициент регрессии, 
и 
-
средние квадратические отклонения
факторного и результативного признака
соответственно.
Результаты работы инструмента «Регрессия» пакета «Анализ данных» Excel
Регрессионная статистика |
|
Множественный R |
0,93 |
R-квадрат |
0,86 |
Нормированный R-квадрат |
0,86 |
Стандартная ошибка |
0,16 |
Наблюдения |
30,00 |
Дисперсионный анализ |
|
|
|
|
|
|
df |
SS |
MS |
F |
Значимость F |
Регрессия |
1,00 |
4,76 |
4,76 |
179,26 |
0,00 |
Остаток |
28,00 |
0,74 |
0,03 |
|
|
Итого |
29,00 |
5,50 |
|
|
|
|
Коэффициенты |
Стандартная ошибка |
t-статистика |
P-Значение |
Нижние 95% |
Верхние 95% |
Y-пересечение |
8,75 |
0,12 |
72,96 |
0,00 |
8,51 |
9,00 |
Переменная X 1 |
0,05 |
0,00 |
13,39 |
0,00 |
0,05 |
0,06 |
