7.2. Определение критической частоты вращения.
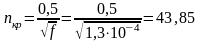с-1;
с-1,
где
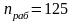об/мин = 12,08 с-1;
-
условие выполняется, см. [3, c.335]
7.3 Рассчет шпоночных соединений
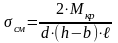, где
-
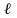длина шпонки,
h - высота шпонки,
b – глубина шпоночного паза.
а) между рабочим колесом и валом
МПа.
= 0,047м; h = 0,008м; b = 0,005м.
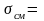11,3
МПа < 800 МПа. Условие выполнено, см [3,
с. 335].
б) между валом и муфтой
МПа.
l= 0,047м; h = 0,008м; b = 0,005м.
МПа < 800 МПа. Условие выполнено, см [3, с. 335].
7.4. Рассчет прочности рабочего колеса.
7.4.1. Площадь поверхности рабочего контакта.
Fсм =l.b = 0,047.0,005 =0,000235 м2.
l,b – длина шпонки и глубина шпоночного паза.
7.4.2. Напряжение смятия в ступице.
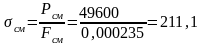МПа.
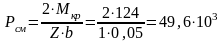Н,
где Z – число передающих штифтов или шпонок. Z = 1.
7.4.3. Запас прочности.
,
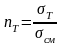где
-
предел текучести для материала Бр.ОФ10-1.
=
340 МПа.
Значение nт должно быть не менее величины запаса статической прочности при рассчете вала(см. выше).
7.4.4 Определяем напряжение в лопасти.
,
где
ΔP-
рассчетный перепад давлений. ΔP
=
=
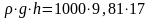166770 Па.
b(R) - ширина лопасти на максимальном радиусе b(R) = 0,017 м,
-
толщина лопасти на максимальном радиусе
=
0,006 м,
МПа.
7.4.5 Нагрузка, действующая на лопасть от центробежных сил на произвольном радиусе R.
,
где
-
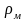плотность материала лопасти.
=
8,76 г/см3 = 8760 кг/м3.
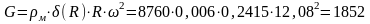Па
7.4.6. Изгибные напряжения в лопасти на произвольном радиусе.
Па.
7.4.7. Суммарные напряжения в лопасти на произвольном радиусе.
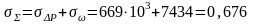МПа.
7.4.8. Коэффициент запаса прочности.
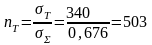
Колесо имеет достаточный запас прочности.
7.4.9. Максимальные напряжения.
МПа
7.4.10. Допустимые напряжения.
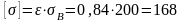МПа.
-
предел прочности материала рабочего
колеса.
=200
МПа.
- коэффициент учитывающий влияние характерных размеров диска. Выбираем по графику на рис. 9.2. [3, с. 328]. = 0,84.
7.4.11. Коэффициент запаса прочности.
Колесо имеет достаточный коэффициент запаса прочности.
7.4.12. Угловая скорость при которой происходит разрушение колеса.
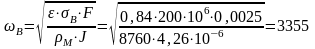рад/с,
где F – площадь половины меридиального сечения диска относительно оси вращения.
F = 0,0025 м2
J – момент инерции половины меридиального сечения диска относительно оси вращения.
J = 4,26.10-6 м3.
7.4.13. Коэффициент запаса прочности.
-
рабочая частота вращения.
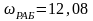
nВ
= 277 удовлетворяет условию
см.
[3, c. 338].
8. Рассчет корпуса.
8.1. Рассчитываем напряжение в элементах корпуса в рамках безмоментной теории оболочек вращения.
,
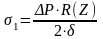
где
ΔP- рассчетный перепад давлений. ΔP = = 166770 Па;
R(Z) – радиус конуса в рассматриваемом сечении.
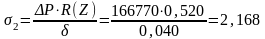МПа.
МПа.
8.2. Определяем эквивалентные напряжения в рассчетном сечении.
8.3. Рассчитываем допустимые напряжения.
Па
-
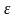коэффициент, учитывающий влияние
характерных размеров(толщины стенки
корпуса в рассчетном сечении δ) на
величину допустимых напряжений, см. [3,
рис. 9.2].
- предел текучести материала Ст.2, = 200 МПа.
8.4. Вычисляем запас прочности..
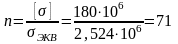
Так как n >3, то это значит, что условие выполнено и выбранный корпус выдержит напряжения.