III. Визначення апріорі невідомих характеристик теоретичного розподілу за результатами експерименту
Основними параметрами теоретичних розподілів є математичне очікування МХ і дисперсія DХ, які апріорі часто бувають невідомі. Вище була дана методика обчислення за емпіричним розподілом середнього значення x і дисперсії S. Ці величини є оцінками для теоретичних значень МХ і DX і, при достатньо великому числі дослідів, можна вважати, що
х ≈МХ і S2≈DX.
Але
так як обсяг вибірки, як правило,
невеликий, то завжди необхідно робити
оцінку написаних вище наближених
рівностей. Ціль статистичної оцінки
параметрів являється знаходження по
вибірковим значенням
і S таких найменших інтервалів, в яких
із заздалегідь заданою вірогідністю
(надійністю) будуть знаходитися МХ і
ОХ. Такі інтервали називаються довірчими.
Так як
і S2 випадкові величини, то ширина
довірчого інтервалу залежить від обсягу
вибірки. Застосовувані в техніці
коефіцієнтів відносного розсіювання
(К) і відносної асиметрії (а) іноді також
являються заздалегідь невідомими. Для
визначення теоретичних значень цих
коефіцієнтів також потрібно за
експериментальними даними визначати
довірчі інтервали.
Розглянемо рішення цих завдань.
1. Визначення довірчих інтервалів для mXі
Визначимо спочатку довірчий інтервал для середнього значення генеральної сукупності.
Нехай маємо вибірку обсягу N з генеральної сукупності з невідомими параметрами MX і σ. Для обчислення довірчого інтервалу використовуємо дані, наведені в табл. 5. В цьому прикладі знайдено, що = – 0,0284 мм та S = 0,0515 мм. Визначаємо виправлене середньоквадратичне відхилення
Визначаємо число ступенів свободи
k=N–1=189
Задаємося надійністю , тобто ймовірністю того, що теоретичне середнє буде знаходитися в довірчому інтервалі.
Покладемо β=0,9. У додатку VII знаходимо, що для k> 120 і β = 0,9 tβ = 1,65.
Визначаємо довірчий інтервал за формулою
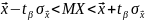
В
даному випадку
=
1,65 • 0,0036 = 0,00594. Тому –0,0284–0,00594 < МХ
<–0,0284 + 0,00594, чи –0,03430 <МХ<–0,02246.
Визначаємо довірчий інтервал для α. Покладемо, що межі поля допуску задані і рівні:
t1
= –0,14; t2 = 0,12. Тоді
;
;
для
Підставляючи
в формулу
замість
межі довірчого інтервалу для MX, отримаємо
межі довірчого інтервалу для αT генеральної
сукупності
;
,
тобто -0,19 <αT<0,096.
Якщо
прийняти β = 0,999, то при k = 199 за додатком
VII знайдемо, що
=
3,29; тоді
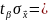0,0118.
Довірчий інтервал для математичного
очікування буде –0,0402 <MX<–0,0166.
Довірчий інтервал для α дорівнює –
0,23 <αT<– 0,051.
Таким чином зі збільшенням надійності межі довірчого інтервалу розширюються.
2. Визначення довірчих інтервалів для s і кт
Для обчислення довірчого інтервалу використовуємо дані попереднього прикладу, для якого маємо: N = 200; к = 199; S = 0,0515 мм.
Задаємося імовірністю знаходження теоретичного ϭ в довірчому інтервалі. Покладемо, що ця ймовірність дорівнює L (q, к) 0,95.
У додатку VIII знаходимо, що при к = 199 і L(q, к) = 0,95 коефіцієнт q = 0,1.
Знаходимо ε = q · S = 0,1 · 0,0515 = 0,00515.
Знаходимо довірчий інтервал для s.
0,0515 - 0,00515 < ϭ<0,0515 + 0,00515.
або 0,04635 <σ <0,05665.
Визначимо довірчий інтервал для Кт.
Підставляючи
в формулу для визначення коефіцієнта
відносного розсіювання К=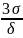
, замість
її верхню та нижню межу, отримаємо
1.07 <Кт< 1,31
Приймемо L (q, к) = 0,995. З додатка VIII отримаємо, що при к = 199 і L(q, к) = 0,995;
q = 0,15.
Тоді ε= q · S = 0,15 · 0,0515 =0,007725; 0,043775 < <0,059225; 1,01 <Кт<1,36.
Необхідна ступінь надійності (імовірності) вибирається для кожного випадку залежно від конкретних умов завдання.
Зауваження. Методика визначення довірчих інтервалів, викладена в п. 1 і 2, застосовується лише для розподілів, які не сильно відхиляються від нормальних.