3. Методика визначення поля допуску за емпіричним розподілом
Багато експериментів проводяться з метою визначення поля допуску, яке характерне для даного технологічного процесу і дає ймовірність ризику (браку) на більш заданого числа. Цю ймовірність будемо надалі позначати через 2β. Зазвичай приймають 2β= 0,0027. Математичне очікування і дисперсія апріорі (до досвіду) невідомі, а є лиш можливість отримати із вибірки значення ͞х і S2 , які є оцінками для MXIDХ.
В цьому випадку приймати за поле допуску величину розмаху R не можна, так як практично граничне поле розсіювання в загальному випадку ніколи не дорівнює розмаху.
Якщо ж за поле допуску приймати значення x ± 3S, то межі поля допуску будуть коливатися від однієї вибірки до іншої, і в одних випадках вони будуть охоплювати більш 99,73% всієї площі, обмеженою кривою, в інших - менше, так як х і S є випадковими величинами.
Завдання полягає в тому, щоб вибране поле допуску охоплювало не менше 99,73% всієї площі, обмеженої генеральною кривою (чи деякого іншого заздалегідь заданого числа). Для цього слід знайти таке l , щоб з заданою імовірністю, близькою до одиниці (надійністю Р), ͞х ± 1S містило не-менш (1-2 β) 100% всієї нормальної генеральної сукупності .
У табл. 7 наведені значення I, обчислені для надійності Р = 0,9; 0,95; 0,99 і для випадків, коли інтервал x ± l S буде охоплювати не менш 99,73; 95 і 90% всієї генеральної сукупності , де ͞х, S - емпіричне середнє і середнє квадратичне відхилення.
Значення коефіцієнта I розраховані для вибірки з нормального сукупності.
Розглянемо приклад визначення поля допуску .
Для емпіричного розподілу визначаємо ͞х і S.
Для даних табл. 5 отримали
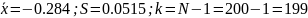k
= N– 1 – 200 –1= 199,
де k– число ступенів свободи.
Задаємося надійністю визначення допуску.
Покладемо, що P = 0,9 .
Задаємося імовірністю 1–2β, тобто задаємо площа генеральної кривої, яка входить в обумовлений нами допуск.
Покладемо 1–2β = 1- 2 • 0,00135 = 0,9973.
За табл. 7 знаходимо, що для Р = 0,9; 1–2β = 0,9973 і k = N–1 = 199 (приймаємо k= 200).
Звідси l= 3,40.
Визначаємо межі поля допуску:
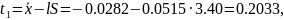
Знаходимо координату середини поля допуску і половини поля допуску:
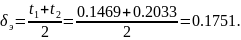
Таким
чином, якщо за поле допуску брати величину
=
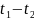0,3502, то з імовірністю 0,9 з усіх майбутніх
спостережень 99,73 % будуть лежати в цьому
інтервалі.
Таблиця значень l для визначення гарантованого поля допуску
Таблиця 7
k = N- 1 число ступенів свободи |
Надійність P=0.9 |
Надійність P=0.95 |
Надійність P=0.99 |
||||||||
1-2β |
1-2β |
1-2β |
|||||||||
0.9973 |
0.95 |
0.9 |
0.9973 |
0.95 |
0.9 |
0.9973 |
0.95 |
0.9 |
|||
4 |
6.76 |
4.18 |
3.51 |
8.26 |
5.11 |
4.29 |
12.80 |
7.92 |
6.64 |
||
5 |
6.07 |
3.74 |
3.14 |
7.17 |
4.44 |
3.72 |
10.31 |
6.38 |
5.35 |
||
6 |
5.60 |
3.47 |
2.91 |
6.50 |
4.02 |
3.38 |
8.91 |
5.51 |
4.62 |
||
7 |
5.80 |
3.27 |
2.75 |
6.05 |
3.74 |
3.14 |
8.01 |
4.95 |
4.15 |
||
8 |
5.07 |
3.13 |
2.63 |
5.72 |
3.54 |
2.97 |
7.38 |
4.56 |
3.83 |
||
9 |
4.89 |
3.02 |
2.54 |
5.48 |
3.39 |
2.84 |
6.91 |
4.27 |
3.59 |
||
10 |
4.75 |
2.94 |
2.47 |
5.28 |
3.26 |
2.74 |
6.55 |
4.05 |
3.40 |
||
12 |
4.54 |
2.81 |
2.36 |
4.99 |
3.08 |
2.59 |
6.03 |
3.73 |
3.13 |
||
14 |
4.39 |
2.72 |
2.28 |
4.78 |
2.96 |
2.49 |
5.67 |
3.52 |
2.95 |
||
16 |
4.28 |
2.65 |
2.22 |
4.62 |
2.86 |
2.40 |
5.41 |
3.35 |
2.81 |
||
18 |
4.19 |
2.59 |
2.17 |
4.50 |
2.79 |
2.34 |
5.21 |
3.22 |
2.70 |
||
20 |
4.11 |
2.54 |
2.14 |
4.39 |
2.72 |
2.29 |
5.05 |
3.12 |
2.62 |
||
25 |
3,98 |
2,46 |
2,07 |
4,20 |
2,61 |
1,19 |
4,76 |
2,94 |
2,47 |
||
30 |
3,89 |
2,40 |
2,02 |
4,10 |
2,54 |
2,13 |
4,57 |
2,82 |
2,37 |
||
40 |
3,78 |
2,33 |
1,95 |
3,94 |
2,44 |
2,05 |
4,31 |
2,67 |
2,24 |
||
50 |
3,69 |
2,28 |
1,91 |
3,84 |
2,37 |
1,99 |
4,15 |
2,57 |
2,16 |
||
60 |
3,63 |
2,25 |
1,89 |
3,76 |
2,33 |
1,96 |
4,05 |
2,50 |
2,10 |
||
70 |
3,59 |
2,22 |
1,86 |
3,70 |
2,30 |
1,93 |
3,96 |
2,45 |
2,06 |
||
80 |
3,55 |
2,20 |
1,85 |
3,66 |
2,27 |
1,91 |
3,90 |
2,41 |
2,02 |
||
90 |
3,53 |
2,18 |
1,83 |
3,63 |
2,25 |
1,89 |
3,84 |
2,38 |
2,00 |
||
100 |
3,51 |
2,17 |
1,82 |
3,60 |
2,23 |
1,87 |
3,80 |
2,35 |
1,98 |
||
200 |
3,40 |
2,10 |
1,76 |
3,47 |
2,14 |
1,80 |
3,59 |
2,22 |
1,87 |
||
300 |
3,25 |
2,07 |
1,74 |
3,41 |
2,11 |
1,77 |
3,50 |
2,17 |
1,82 |
||
400 |
3,32 |
2,06 |
1,73 |
3,37 |
2,08 |
1,75 |
3,45 |
2,14 |
1,79 |
||
500 |
3,30 |
2,05 |
1,72 |
3,35 |
2,07 |
1,74 |
3,41 |
2,12 |
1,78 |
||
600 |
3,29 |
2,04 |
1,71 |
3,33 |
2,06 |
1,73 |
3,39 |
2,10 |
1,76 |
||
800 |
3,27 |
2,03 |
1,70 |
3,30 |
2,05 |
1,72 |
3,36 |
2,08 |
1,75 |
||
1000 |
3,26 |
2,02 |
1,70 |
3,29 |
2,04 |
1,71 |
3,33 |
2,07 |
1,74 |
||