9. Вирівняння за узагальненою кривою пуассона-шарльє
Значення вирівняних частот визначаються за формулами:
,
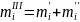д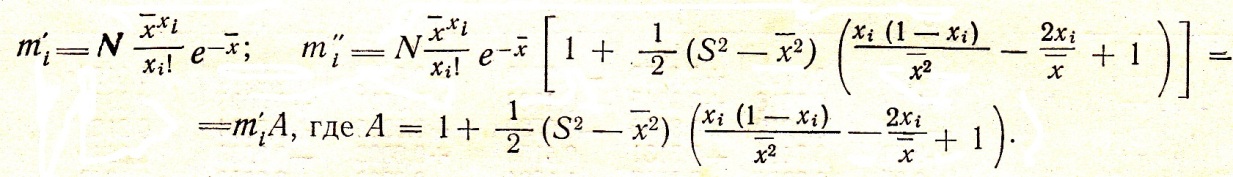
е
Вирівнювання розглянемо на прикладі [12] (табл. 10).
Таблиця 10
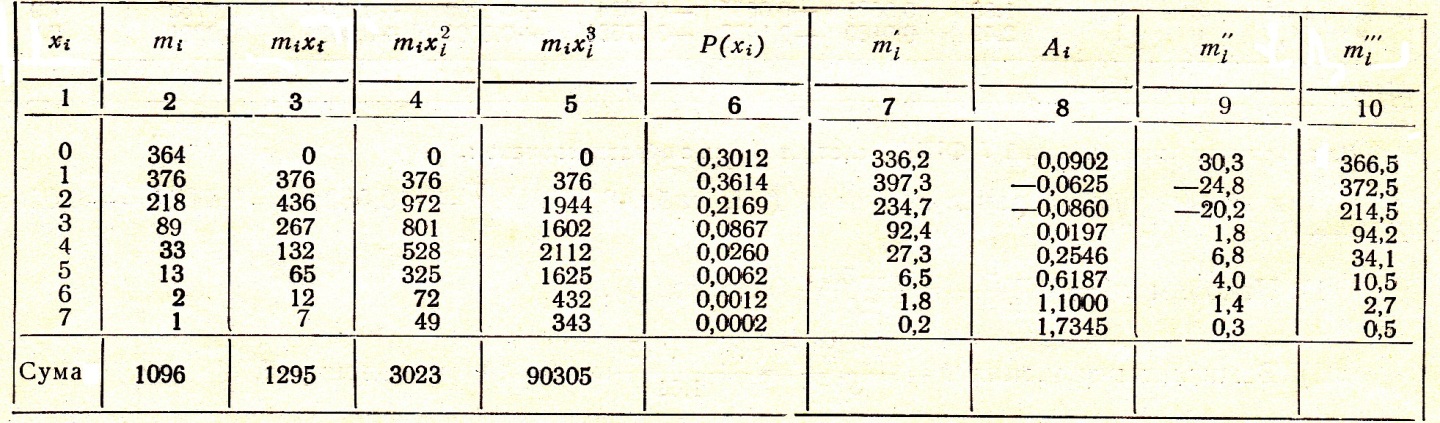
Розрахунки проводимо в наступній послідовності:
1) Визначаємо центральні і початкові моменти
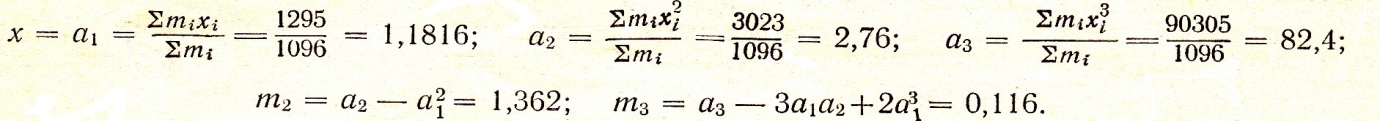
Для
закону Пуассона
В даному випадку
значно відрізняється від
.
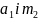Тому необхідно розрахувати поправку
Шарлье*.
2)
Для
за додатком XVII знаходимо
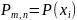і заповнюємо колонку 6.
3)
Перемножуючи значення
на N= 1096, отримаємо значення частот,
вирівняні за законом Пуассона (колонка
7).
4) Підставивши значення Sі в (a) і зробивши перетворення, отримаємо
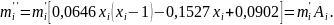
Після визначення значення А заповнюємо колонку 8.
5)
В колонці 9 дані значення
6)
В колонці 10 дані
.
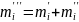На
рис. 10 дані графіки емпіричної кривої
(
,
вирівняної за законом Пуассона (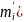
і за законом Пуассона–Шарльє (
Рис. 10
10. Параболічне вирівнювання за способом найменших квадратів (метод чебишева)
В ряді випадків виявляється зручним не підбирати різні функції до емпіричного розподілу, а вирівняти його за параболою в тій чи іншій мірі.
Існує декілька способів параболічного вирівнювання статистичних кривих. Найбільш досконалим являється спосіб Чебишева. За цим способом вдається підвищувати, використовуючи дані попередніх розрахунків, порядок (степінь) параболи. Завдяки наявності таблиць, розрахунки являються найбільш легкими.
Нехай маємо емпіричну криву, котру необхідно вирівняти за параболою в тій чи іншій мірі.
Розглянемо випадок, коли значення незалежної змінної являються рівновіддаленими,
тобто
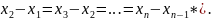
Р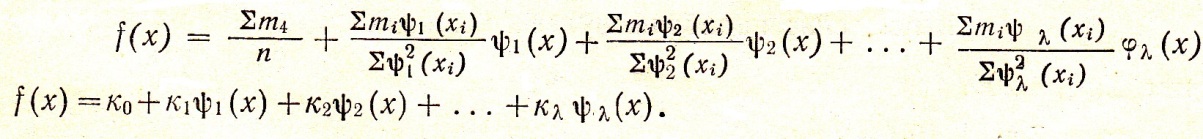
озрахунок
параболи потрібного порядку заклечається
в поступовому
розрахунку членів ряду Чебишева [10]
*Якщо
вводиться поправка Шарльє, то моменти
в розрахунках не використовується. Тому
в тих випадках, коли потрібне введення
поправки Шарльє очевидна зарані,
розраховувати
не потрібно.
**Загальний випадок, коли значення можуть відрізнятися одне від іншого на різну величину, розглянутий в розділі VII.
Значення
для того чи іншого значення n– числа
інтегралів (значень випадкової величини)
розраховані раніше і наведені в додатку
ХХ. Ці таблиці дають можливість знаходити
параболу до 5-го порядку.
Для
зручності розрахунків в додатку ХХ дані
цілі числа
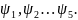В заголовках таблиць указані коефіцієнти
за
допомогою котрих виконується перехід
від дробових чисел до цілих.
Тому
необхідно для отримання дійсних чисел
знайдене
із таблиць умножити на
,
тобто умножити на похідну коефіцієнта
,
що вказаний в заголовку λ-го стовпця
таблиць (додатку ХХ) даного значення n
на вираз
котре
рівне
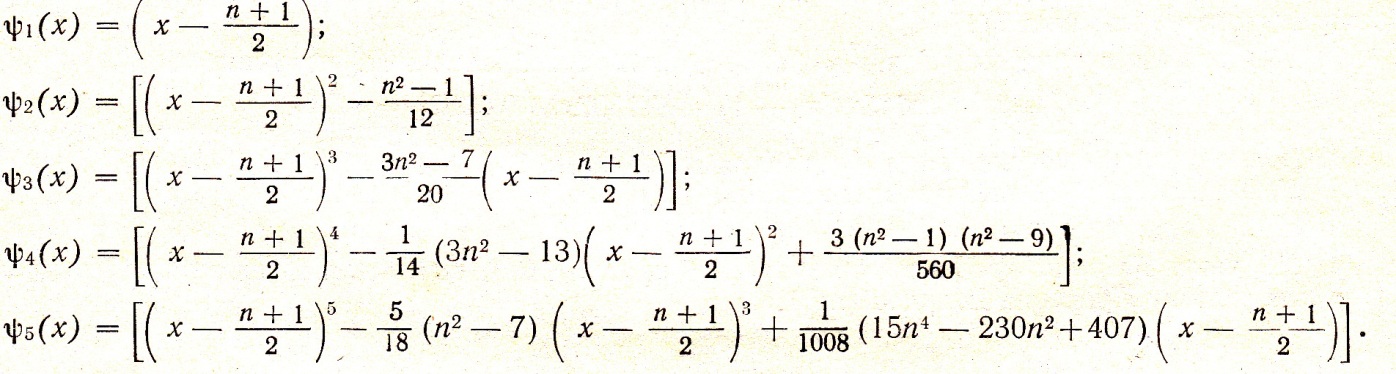
П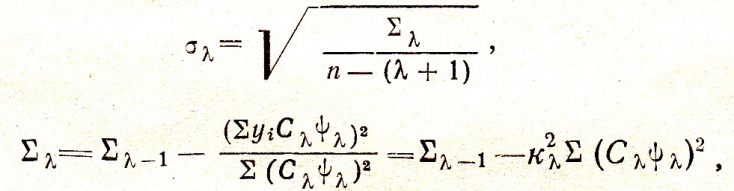
омилки
приближення параболи розраховуються
за формулою
де
при
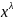даної
параболи
Послідовність розрахунків розглянемо на числових даних, приведених в табл. 11.
Таблиця 11
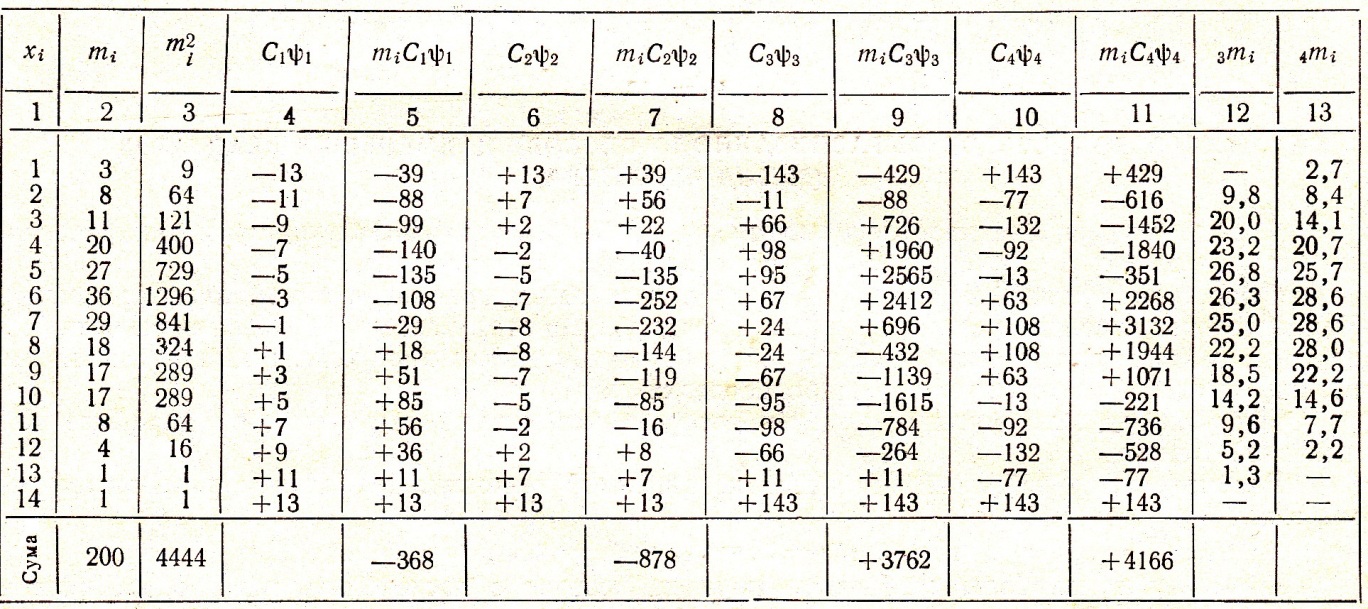
Розрахунок параболи нульового порядку
Знаходимо
Σ
Знаходимо
Складаємо
рівняння нульового порядку
( індекс перед
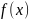тут
і в подальшому вказують на порядок
кривої)
Знаходимо суму квадратів різниць між значеннями функції, що спостерігаються і рівнянням нульового порядку, що визначаються.
Розраховуємо основну помилку
Розраховуємо параболу 1-го порядку
За
додатком ХХ знаходимо для n = 14 значення
.
Розраховуємо
відношення
,
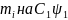котрі заносимо в колонку 5. Знаходимо
суму цих відношень.
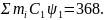
Д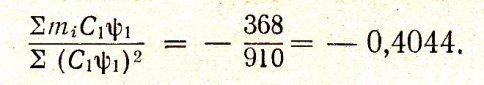
ілимо
знайдену суму на суму квадрантів
котра дається знизу першої колонки
додатку ХХ (для n = 14).
Перемножуємо
отриману частку на
Із додатку ХХ видно, що в першій колонці
коефіцієнт при
рівний
(для n = 14).
Знайдений результат добавляємо до правої частини рівняння параболи нульового порядку.
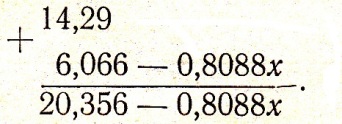
Пишемо
рівняння параболи 1-го порядку 1
.
Розраховуємо основну помилку
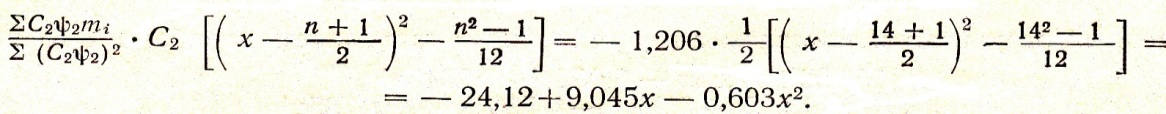
Розраховуємо параболу 2-го порядку
Виписуємо
значення
в колонку 6 табл.11 із додатку ХХ для n =
14.
Розраховуємо значення на , котрі заносимо в колонку 7. Знаходимо суму цих значень.
Σ
Ділимо
цю суму на Σ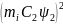
,
показану знизу 2-го стовпця таблиці
додатку ХХ
(для n = 14)
Множимо
отриману частку на
І
з
2-ї колонки таблиці додатку ХХ бачимо,
що
З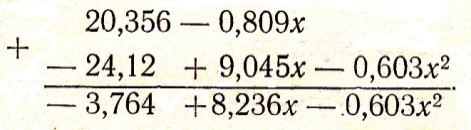
найдений
результат складуємо алгебраїчно з
рівнянням параболи 1-го порядку.
Пишемо рівняння параболи 2-го порядку
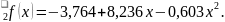
Розраховуємо
основну помилку:
991,57-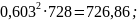
Помилка σ зменшилась. Продовжуємо розрахунки.
Розраховуємо параболу 3-го порядку
Виписуємо
значення
в
колонку 8 табл. 11 із додатку ХХ.
Розраховуємо
і
заносимо в колонку 9. Потім знаходимо
суму
Σ
Ділимо
цю суму на
,
що показана знизу 3-го стовпця таблиці
додатку ХХ
для n = 14.
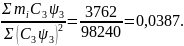
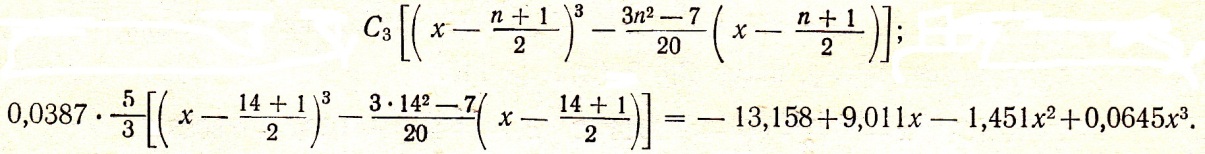
Знайдений результат складуємо алгебраїчно з рівнянням параболи 2-го порядку.
Пишемо
рівняння параболи 3-го порядку
Розраховуємо
основну помилку:
Розраховуємо параболу 4-го порядку
Виписуємо
значення
в
колонку 10 табл. 11 із додатку ХХдля n = 14.
Розраховуємо
значення
на
і записуємов колонку 11. Потім знаходимо
суму Σ
Ділимо
цю суму на
,
що показана в кінці 4-го стовпця таблиці
додатку ХХ
(n = 14).
Множимо отриману частку на
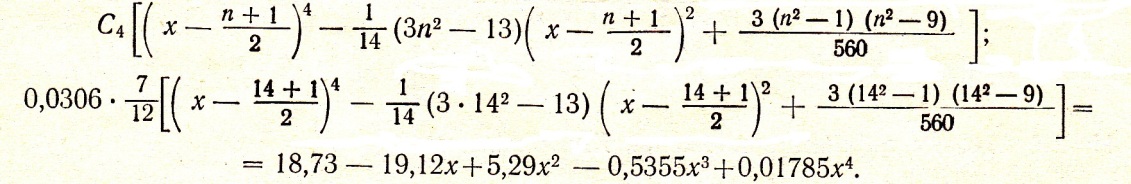
Знайдений результат складуємо алгебраїчно з рівнянням параболи 3-го порядку
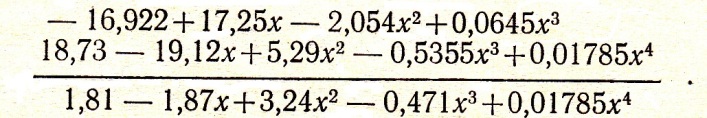
Пишемо рівняння параболи 4-го порядку
Визначаємо основну похибку:
;
;
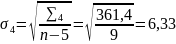Так
як
незначно відрізняється від
,
то обчислювати параболу 5-го порядку
нема необхідності.
В колонках 12 і 13 приведені значення 3miі 4m4 , розраховані за рівняннями парабол 3-го і 4-го порядків.
Ці частоти визначаються шляхом підстановки в знайдені рівняння значення х=1,2,3,…14.
Наприклад, рівняння 4-го порядку має вигляд:
4f(x)=1,81-1,87+3,24x2-0,471x3+0,01785x4.
Значення 4miбудуть рівні:
4m1 =1,81-1,87∙1+3,24∙12-0,471∙13+0,01785∙14=2,7
4m2 =1,81-1,87∙2+3,24∙22-0,471∙23+0,01785∙24=8,4
4m3 =1,81-1,87∙3+3,24∙32-0,471∙33+0,01785∙34=14,1 і т.д.
Криві mi, 3mi , 4mi показані на рис.11.
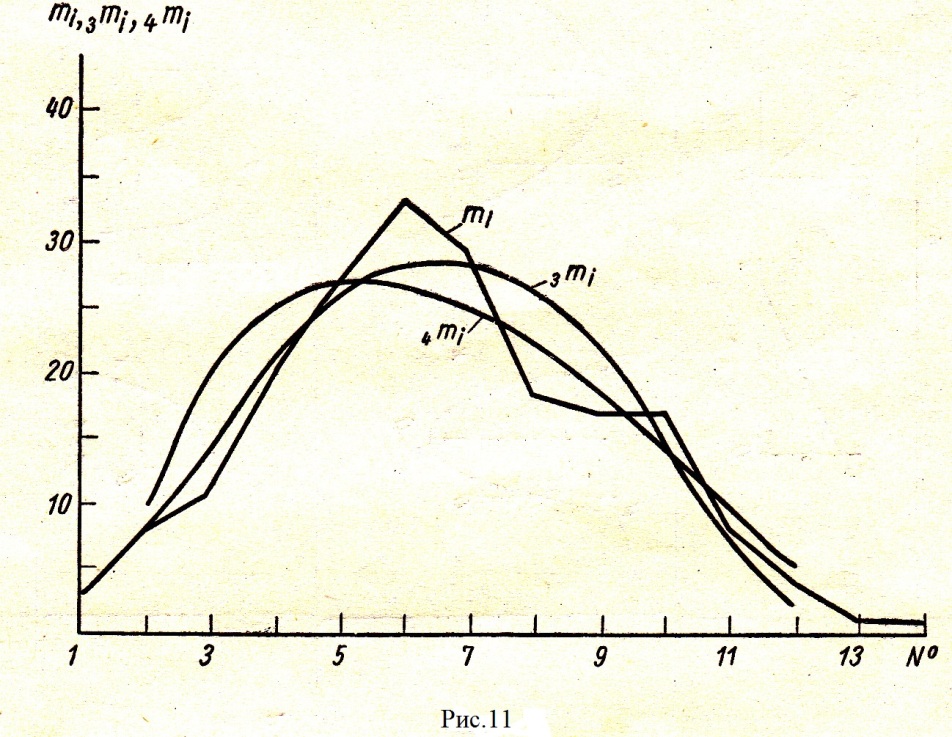
Оцінка погодження емпіричних і теоретичних кривих повинна проводитись по критерію погодження Пірсона х2.
