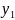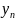3.Оцінка випадкової розбіжної між двома вибірковими середніми

Припустимо, що маємо дві вибірки об'ємів і . По цих вибірках знаходимо середнє значення і середні квадратичні відхилення . Необхідно оцінити, чи суттєво відрізняється , або це відхилення є випадковим, і обидві вибірки належать до однієї генеральної сукупності.

Для вирішення завдання скористаємося розподілом Ст’юдента.

Розглянемо приклад.

Нехай отримали вибірки А і В.

А– 35,50; 32,66; 30,56; 36,63; 42,28; 34,78; 40,20

В–43,44; 47,51; 53,80.

Потрібно визначити, чи є розбіжність між середніми значеннями цих двох вибірок істотною.

Для обох вибірок обчислюємо величини х і S.

Число спостережень

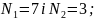
Обчислюємо величини:

Обчислюємо величину S

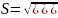
Знаходимо модуль різниці (абсолютну величину різниці між емпіричними середніми)

Визначаємо

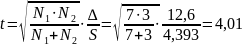
За додатком IX знаходимо, що для к = і t = 4 S(t) = 0998.

Знаходимо ймовірність того, що отримана різниця між двома вибірковими середньо випадковою.

P(

Так як вірогідність Р =0,004 <0,05, то розбіжність між двома середніми істотна, і їх не можна вважати вибірками з однієї генеральної сукупності.

Розглянемо також спосіб оцінки випадковості розбіжності двох вибіркових середніх, запропонований Романовським .

Величина t, розраховується за тими ж формулами, що і в попередніх випадках, має наступні параметри розподілу.

Звідси за правилом “ трьох сигм ” отримуємо, що якщо розходження не випадкові і якщо 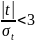– розходження випадкові.

Проведемо оцінку вагомості розходжень між середніми за способом Романовського для попереднього прикладу:

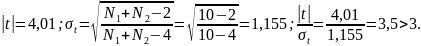
Відповідно, розходження не випадкове, а суттєве.

Цей спосіб порівняння середніх слід використовувати в тому випадку, коли потрібно і достатньо лише вияснити, що ймовірність розходження вибіркових середніх менше чи більше 0,0027.

4. Оцінка випадкової розбіжності між двома вибірковими дисперсіями

Нехай маємо дві вибірки А і В. Для обох вибірок розраховуємо емпіричні дисперсії і . Необхідно оцінити, випадкові чи не випадкові розходження між ними, тобто чи належать вони одній генеральній сукупності. Вибірки рахуємо незалежно.

Для вирішення цієї задачі можна скористуватися розподілом величини Р. Фішера.

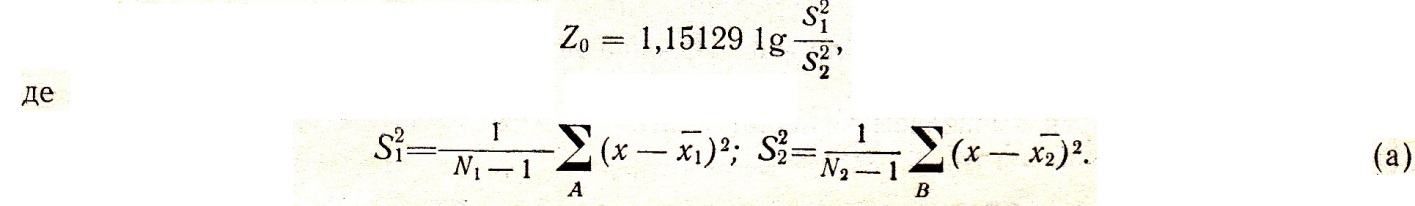
Послідовність розрахунків розглянемо на попередньому прикладі, де

Розраховуємо і :

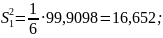
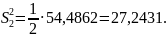
Знаходимо . Так як додаток VІІ дає лиш додаткові значення Z, то за , потрібно приймати більшу дисперсію, а за – меншу.

За додатком ХІІ знаходимо, що для 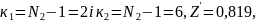що більше

Так як , то з ймовірністю більше 0,05 розходження між дисперсіями можна вважати не важливими, випадковими, а вибірки приналежні одній генеральній сукупності.

В тих випадках, коли виявиться, що 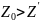, то розходження невипадкові і вибірки не належать одній генеральній сукупності.

Приведемо також більш простий критерій Романовського, котрий дає майже ті результати, що і критерій Фішера. Цим критерієм можна користуватися, коли об’єм вибірок більше 5.

Введемо величину

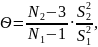
де , – об’єм вибірок;

– вибіркові дисперсії, розраховуємо як і раніше за формулами (а).

Якщо вибірки належать одній сукупності і незалежні, то

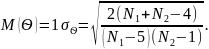Якщо , то розбіжність між і не випадково, і вибірки зроблені з різних

генеральних сукупностей. Якщо ж   то розбіжність-можна вважати випадковою. Розглянемо попередній приклад: . Обчислюємо

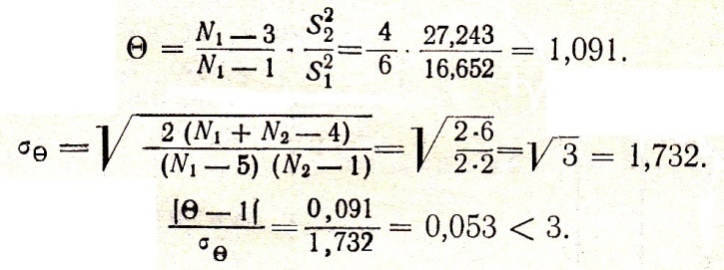
Отже, і не відрізняються суттєво один від іншого. Такий же результат дало порівняння за критерієм Фішера.

5.СЕРЕДНЄ АРЕФМЕТИЧНЕ І ДИСПЕРСІЯ ДЛЯ ДВОХ ОБ'ЄДНАНИХ ВИБІРОК Нехай маємо дві вибірки обсягів і . За вище наведеним критеріям визначили, що вони належать до однієї генеральної сукупності; ці вибірки можна об'єднувати. Середнє значення й дисперсія об'єднаної вибірки визначаються за формулами

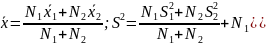
Розглянемо приклад

(1–а вибірка)

(2–а вибірка)

Для об'єднаної вибірки =

.

VII. ВСТАНОВЛЕННЯ ВИДУ ЗАЛЕЖНОГО МІЖ ДВОМА ЗМІННИМИ ВЕЛИЧИНАМИ Іноді необхідно з'ясувати вид залежності між двома змінними величинами, яка може бути функціональною або стохастичною.

Функціонально залежними є такі величини, у яких кожному значенню однієї величини відповідає цілком певне (найчастіше одне) значення іншої величини (величина зносу різця від часу, залежність тиску від температури, величина похибки розміру виробу від температури, властивості сплавів від процентного вмісту в ньому того або іншого елемента та ін.). Стохастично залежними називаються такі величини, у яких різним значенням однієї величини відповідають різні закони розподілу іншої величини. Окремим випадком стохастичної залежності є корелятивна залежність. Вона полягає в тому випадку, коли кожному значенню однієї величини відповідають різні середні значення іншої величини (розміри виробів оброблюваних одночасно на одному верстаті, одним інструментом, в одному пристосуванні та ін.).

Зупинимося на вирівнюванні емпіричних даних за деякими видами функціональних залежностей і на методиці визначення коефіцієнта кореляції при корелятивній залежності.

Для встановлення виду функціональної залежності експеримент,проводиться таким чином, що для кожного значення однієї ознаки (незалежне змінне x) визначається значення іншої ознаки (залежної змінної y), а результати заносяться в таблицю виду.

№	1	2	3	…	n
Температура Розмір виробу				… …

З а цими даними будується графік залежності між величинами х і у (рис. 8). Отриману ламану лінію необхідно вирівняти по найбільш близькій до неї теоретичної кривої.