Національний університет біоресурсів і природокористування україни

Кафедра технології

лісогосподарського виробництва

Кафедра

надійності техніки

Методичні вказівки до практичних занять з дисципліни

«Оптимізація підприємства лісового комплексу»

Частина 5. (Оптимізація обчислень результатів експерименту)

для підготовки фахівців освітньо-кваліфікаційного рівня «Магістр»

спеціальність 8.05050303 «Обладнання лісового комплексу»

КИЇВ 2012

УДК 630.1:631.3

Методичні вказівки до лабораторних робіт з дисциплін «Оптимізація підприємства лісового комплексу» та «Надійність обладнання лісового комплексу». Матеріали викладені у п’ятьох частинах. В п’ятій частині методичних вказівок викладені матеріали до розрахунків експериментальних досліджень в прикладах. Вони можуть бути використані для самостійної роботи студентів та для обробки експериментальних даних під час написання магістерських робіт.

Рекомендовано Вченою радою факультету конструювання та дизайну машин і систем природокористування Національного університету біоресурсів і природокористування України.

Укладачі: доцент С.В. Маслай, доцент А.В. Новицький

Рецензенти: доцент О.А. Грушанський., доцент З.В. Ружило

Навчальне видання

МТОДИЧНІ ВКАЗІВКИ

до виконання лабораторних робіт:

«Оптимізація підприємства лісового комплексу»

для студентів зі спеціальностей

8.05050303 – Обладнання лісового комплексу ”

Укладачі: МАСЛАЙ СЕРГІЙ ВОЛОДИМИРОВИЧ

НОВИЦЬКИЙ АНДРІЙ ВАЛЕНТИНОВИЧ

Зав. видавничим центром НУБіП України А.П.Колесніков

Видання здійснено за авторським редагуванням

Підписано до друку 26.11.12. Формат 60х84 1/16.

ЗМІСТ

Вступ 7

I . Основні поняття та визначення теорій математичної статистики 8

II. Методика побудови емпіричної кривої. Обчислення її параметрів і характеристик 17

1.Побудова емпіричної кривої 17

2.Техніка обчислень параметрів емпіричного розподілу 20

3.Методика визначення поля допуску по емпіричному розподілу 23

4.Обчислення коефіцієнтів відносної асиметрії і відносного розсіювання 26

5.Критерії для неприйняття спостережень , що різко виділяються

від (помилок вимірювань) 27

III. Визначення апріорі невідомих характеристик теоретичного розподілу за результатами експерименту 30

1.Визначення довірчих інтервалів для M xi 30

2.Визначення довірчих інтервалів для КT 31

3.Визначення математичного сподівання і дисперсії функцій випадкових величин 32

IV. Порівняння емпіричних характеристик розподілу з теоретичними 33

1. Оцінка випадкової розбіжності між заданим математичним очікуванням і вибірковим середнім 34

2. Оцінка випадкової розбіжності між теоретичними та емпіричними середніми квадратичними відхиленнями 35

3. Оцінка випадкової розбіжності між емпіричними і теоретичними значеннями коефіцієнтів α і К 36

а) Оцінка випадкової розбіжності між αт і αе 36

б) Оцінка випадкової розбіжності між КТ і Ке 37

в) Визначення обсягу вибірки для отримання α і К заданої точності. 37

V. Функції щільності теоретичних і емпіричних розподілів 38

1. Підбір теоретичної функції для емпіричного розподілу 38

2. Вибір можливих функцій щільності ймовірностей 38

3. Вирівнювання емпіричного розподілу по гіпотетичним

теоретичним даним 39

4. Порівняння емпіричних і теоретичних функцій розподілу частот по критеріям згоди 41

а) Критерій згоди Пірсона 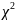41

б) Критерій Колмогорова λ 42

5. Перевірка правильності теоретичного висновку про вид функції і значення її параметрів за результатами експерименту 43

VII Способи визначення належності двох вибірок до однієї генеральної сукупності 45

1. Порівняння двох емпіричних вибірок великого обсягу 45

2. Порівняння двох вибірок невеликого обсягу 47

3. Оцінка випадкової розбіжності між двома вибірковими середніми 50

4. Оцінка випадкової розбіжності між двома вибірковими дисперсіями 52

5. Середнє арифметичне і дисперсія для двох об'єднаних вибірок 53

VII. Встановлення виду залежностей між двома змінними величинами 54

1. Функціональна залежність 55

2. Кореляційна залежність 59

Додатки I-II до РТМ 44-62 68

I. Деякі теоретичні закони розподілу 68 Вирівнювання емпіричних розподілів 78

1. Вирівнювання за законом Максвелла двомірному розподілі 78

2. Вирівнювання за законом модуля різниці 80

3. Вирівнювання за законом рівної ймовірності 82

4. Вирівнювання за композиційному закону Гаусса 84

5. Вирівнювання по композиційному закону Гаусса і рівномірно зростаючої ймовірності 88

6.Вирівнювання по композиційному закону Гаусса і рівномірно спадної ймовірності . 91

7.Вирівнювання за законом рідкісних подій (Пуассона) . 94

8. Вирівнювання по нормальної кривої Лапласа – Шарльє 96

9. Вирівнювання по узагальненої кривої Пуассона – Шарльє . 98

10.Параболічне вирівнювання за способом найменших квадратів (метод Чебишева) 100

III. Графіки деяких елементарних функцій . 108

IV. Вирівнювання емпіричної кривої залежних змінних величин 110

1. Вирівнювання за показовою функцією 110

2. Вирівнювання за степеневої функцією 112

3. Вирівнювання за логарифмічною кривою 113

V. Щільність ймовірності нормального розподілу 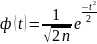115

VI. Значення функції 115

VII. Розподіл нормованих відхилень в малій вибірці 117 Таблиця ймовірностей L(q, k)=P(S- ε<ϭ<S+ ε) ;

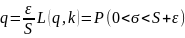118

IX. Таблиця ймовірностей S(t) за критерієм t Стьюдента 119

X. Таблиця ймовірностей Р за критерієм К Пірсона Х2 121

XI. Таблиця значень Р (λ) критерієм Колмогорова 122

XII. Таблиця значень Z розподілу Фішера 123

XIII. Таблиця значення 124

XIV. Значення функції 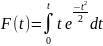125

XV. Значення p0 для величин λ функції модуля різноманітності 126

XVI. Параметри функції розподілу модуля різноманітності 126

XVII; Інтегральна функція F(р) модуля різноманітності 127

XVIII. Розподіл Пуассона Pm, n= . 129

Третя і четверта похідні 132

XX. Коефіцієнти поліномів Чебишева 136

XXI. Використана література 139

В С Т У П

При виконанні науково-дослідних робіт дуже часто доводиться звертатися до емпіричних даних. Так, наприклад, може виникнути необхідність визначити шляхом експерименту практичні значення різних параметрів або характеристик машин, деталей або їх матеріалів. До таких характеристик можна віднести: точність роботи окремих механізмів машини, точність відносного розташування вузлів машини, величини зазорів, істотних для роботи машини, лінійні або кутові розміри деталей, вагу деталей, об’єми тіл, механічні характеристики матеріалу деталей (твердість, межа міцності, межа текучості) та інші. Постановка експериментальної роботи може бути підпорядкована вирішенню різних завдань.

Перша область, в якій шляхом експерименту можуть вирішуватися різні завдання, охоплює випадок, коли чисельні значення характеристик досліджуваного параметра виробу заздалегідь невідомі. У таких випадках дослідник отримує цікаві йому характеристики із експериментів. При цьому іноді дослідника можуть цікавити тільки деякі окремі характеристики цього параметра, наприклад, поле розсіювання, середнє значення, дисперсія. У ряді ж випадків дослідник може шукати більш повну характеристику досліджуваного параметра, наприклад, у вигляді аналітичної функції, яка описує визначені закономірності, притаманні даному параметру.

Друга область, в якій шляхом експерименту можуть вирішуватися різні завдання, охоплює випадки, коли чисельні значення характеристик досліджуваного параметра або навіть аналітична функція заздалегідь відомі (задані або отримані теоретичними розрахунками). В цих випадках дослідник порівнює результати експерименту з теоретичними значеннями характеристик або з відомою аналітичною функцією і робить відповідні заключення.

Досліджувані параметри машин або їх деталей в ряді випадків являють собою незалежні один від одного випадкові величини. Іноді ці параметри пов'язані між собою якоюсь функціональної або корелятивної залежністю. Знаходження виду зв'язку між двома параметрами машини або її деталей є третьою областю експериментальних робіт. Результат експерименту, незалежно від його цільового призначення, отримується у вигляді набору чисел. Для того, щоб скористатися результатами проведеного досвіду і робити на підставі його якісь узагальнення і висновки, потрібно попередньо провести статистичну обробку всіх матеріалів експерименту. Статистична обробка емпіричних даних по суті зводиться (у загальному вигляді) до наступного:

1. Обчислення визначених характеристик досліджуваного параметра машини.

2. Визначення теоретичних значень характеристик за їх експериментальним значенням.

3. Порівняння за певними критеріями експериментальних значень характеристик із заданими теоретичними.

4. Вирівнювання емпіричного розподілу за прийнятим (або заданому) теоретичним.

5. Порівняння емпіричних і теоретичних функцій за певними критеріями узгодженості.

6. Встановлення виду залежності між двома випадковими величинами.

При складанні даної методики не ставилася мета дати повне і послідовне викладення питання застосування теорії ймовірностей та математичної статистики. Завдання полягало в тому , щоб з усього великого матеріалу з математичної статистики виділити і зібрати в одному місці тільки ті її розділи, які найбільш часто можуть використовуватися в машинобудуванні. Завдання полягало також у тому, щоб викласти весь матеріал в доступній для інженера формі і ілюструвати прикладами.

Наведені приклади статистичної обробки відносяться головним чином, до питань точності виробництва. Проте викладена в роботі методика може бути використана при статистичній обробці результатів експериментальних досліджень у будь-який інший області.