2.5 Законы сопротивления гладких труб

Из (2.29) и (2.30), исключив скорость на оси трубы, получим:

(2.35)

Из формулы (2.15) определим перепад давления:

(2.36)

где d = 2 R.

Исключив с помощью (2.36) величину в формуле (2.7), найдем коэффициент гидросопротивления:

(2.37)

Используя (2.21), исключим величину . После преобразований получим:

(2.38)

Величину, входящую под знак логарифма в (2.35), преобразуем к виду:

(2.39)

где .

Подставив (2.38) в (2.35) и учтя (2.39), получим универсальный закон сопротивления:

(2.40)

Для лучшего совпадения с опытом Никурадзе несколько изменил коэффициенты в (2.40):

(2.41)

В литературе эту формулу называют формулой Никурадзе-Прандтля для гладких труб. В явном виде закон сопротивления записывается с помощью аппроксимации:

(2.42)

При числах часто пользуются формулой Блазиуса, полученной эмпирическим путём:

(2.43)

Формула П.К. Конакова справедлива в широком диапазоне чисел , так как она является аппроксимацией универсального закона сопротивления в явном виде:

(2.44)

2.6 Течение жидкости в шероховатых трубах

Все технические трубы имеют шероховатые стенки. Техническая шероховатость имеет самые различные размеры, геометрические формы и распределение по поверхности. Это чрезвычайно сильно затрудняет её количественную оценку и её влияние на движение жидкости. Для более простой оценки шероховатости вводят понятие песочной или эквивалентной шероховатости, под которой понимают такую высоту выступов песчинок , которая создаёт сопротивление, равное действительному сопротивлению данного трубопровода.

Влияние песочной шероховатости подробно изучено И.И. Никурадзе. Он оклеивал стенки труб песком с зернами определённого размера, расположенными очень плотно. Путем выбора различных диаметров труб и различных зерен песка, параметр , где R-радиус трубы, варьировался в диапазоне 1/500 – 1/15. Характер поведения кривых коэффициента сопротивления показан на рисунке 2.4.

П ри ламинарном течении все шероховатые трубы имеют такое же сопротивление, что и гладкие. Это объясняется тем, что вязкая жидкость заполняет впадины между бугорками и ламинарность течения не нарушается. Критическое число и сопротивление в переходной области также практически не зависят от шероховатости.

При турбулентном режиме течения следует различать три режима:

• режим без проявления шероховатости, при котором:

Размеры зерен столь малы, что все выступы элементов шероховатости лежат внутри ламинарного подслоя . Такие трубы называются гидравлически гладкими;

• переходный режим, при котором:

Этот режим наступает при увеличении числа Re и уменьшении при этом толщины ламинарного подслоя , когда гребешки шероховатости частично попадают в область турбулентного течения , вызывая дополнительные завихрения и потери энергии;

• режим с полным проявлением шероховатости, при котором:

Все элементы шероховатости выступают из ламинарного подслоя . Сопротивление обусловлено в основном сопротивлением формы отдельных элементов шероховатости. Этот режим часто называют еще автомодельным относительно числа Re и режимом квадратичной зависимости гидросопротивления от скорости .

Для определения коэффициента гидросопротивления шероховатых труб получена интерполяционная формула:

(2.45)

При она переходит в формулу(2.41). При - в формулу Никурадзе для шероховатых труб:

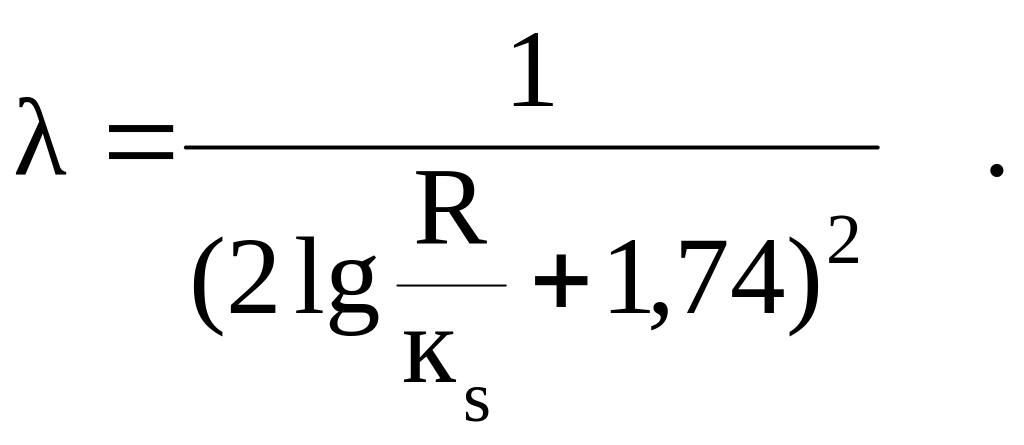(2.46)

Очень часто пользуются формулой Шифринсона:

(2.47)

Для всех турбулентных режимов Альтшуль предложил приближенную формулу:

(2.48)

При она практически совпадает с формулой (2.43), а при - с формулой (2.47).

Как уже отмечалось, расчет труб с технической шероховатостью производят с помощью формул, в которых используется понятие эквивалентной шероховатости. Если, например, подставить опытное значение в формулу (2.46), то для трубы с технической шероховатостью можно найти соответствующее значение эквивалентной шероховатости. Значения для технических труб приведены в справочниках по гидравлическим сопротивлениям.

Следует отметить, что в технически шероховатых трубах переход от режима без проявления шероховатости при малых числах Re к режиму с полным проявлением шероховатости при больших числах Re происходит более постепенно, чем в трубах с песочной шероховатостью.