Високий рівень
1. 1) Обчислити
.
2) Спростити
.
3) Обчислити значення виразу 107·(2,4 106 – 3,1 105) і записати його у стандартному вигляді.
2. Довести, що значення виразу (5x–100 – 1)(5x–100 + 1) – (5x–100 + 2)2 + + 20x–100 не залежить від значення змінної x.
3. Спростити вираз
.
№ 84. Варіант 4.
Середній рівень
1. 1) Обчислити
(–9)–2;
;
.
2) Подати
у вигляді степеня:
;
;
a–9 a12;
m–4 : m–11;
(b2)–10.
3) Подати у вигляді дробу, що не містить степенів з від’ємними показниками: –14a–15; 9a–8b2.
4) Записати в десятковому вигляді число: 3,125 106; 2,9 10–4.
2. 1) Подати у вигляді
степеня з основою 2 число:
.
2) Спростити вираз:
а) 0,2ab–4 8a–9b–3; б) 7a–8 (a–4)–3.
3. 1) Обчислити
;
–5–3; (–0,5)–2.
2) Перетворити у раціональний дріб вираз a–3 – a–2.
3) Записати у стандартному вигляді число: 913000000; 0,0000074.
Достатній рівень
1. 1) Знайти значення виразу:
а)
–2–3 + 
;
б)
.
2) Спростити
вираз
.
3) Подати у вигляді раціонального дробу вираз (2x + 3x–1) : (3x – 2x–1).
4) Записати
у стандартному вигляді число:
;
.
2. Знайти значення виразу
.
3. Обчислити суму 2,87 104 + 7,3 105 і записати її у стандартному вигляді.
Високий рівень
1. 1) Обчислити
.
2) Спростити
.
3) Обчислити значення виразу (7,2 105 – 2,1 104) 106 і записати його у стандартному вигляді.
2. Спростити вираз (a–4 + b–4)(a–2 + b–2)(a–1 + b–1)(a–1 – b–1).
3. Спростити вираз
.
№ 85. Варіант 5.
Середній рівень
1. 1) Обчислити:
(–8)–2;
;
.
2) Подати
у вигляді степеня:
;
;
x–21 x19;
a–6 : a2; (y3)–15.
3) Подати у вигляді дробу, що не містить степенів з від’ємними показниками: –25a–7; 7x–5y4.
4) Записати в десятковому вигляді число: 3,024 106; 1,03 10–3.
2. 1) Подати у вигляді
степеня з основою 3 число:
.
2) Спростити вираз:
а) 0,6x2y–10 5x–5y–3; б) c3 9(c–2)5.
3. 1) Обчислити:
;
2–5; (–0,6)–3.
2) Перетворити у раціональний дріб вираз a–4 + a–3.
3) Записати у стандартному вигляді число: 913000000; 0,0000074.
Достатній рівень
1. 1) Знайти значення виразу:
а)
;
б)
.
2) Спростити
вираз
.
3) Подати у вигляді раціонального дробу вираз (3a – 2b–1) (4a3 – 5b2).
4) Записати у стандартному вигляді число: 0,0034 1017; 55,3 10–12.
2. Знайти значення виразу
.
3. Обчислити суму 3,1 10–3 + 4,2 10–4 і записати її у стандартному вигляді.
Високий рівень
1. 1) Обчислити
.
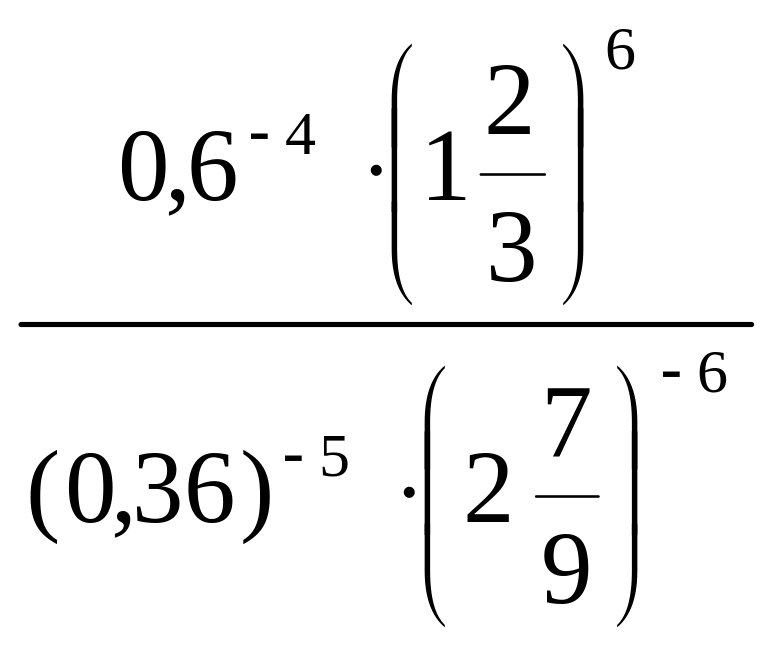2) Спростити
.
3) Записати у стандартному вигляді число 2000004.
2. Спростити вираз
.
3. Спростити вираз
.
№ 86. Варіант 6.
Середній рівень
1. 1) Обчислити:
(–6)–2;
;
.
2) Подати
у вигляді степеня:
;
;
a–31 a29;
m–1 : m–7;
(b–6)–4.
3) Подати вираз у вигляді дробу, що не містить степенів з від’ємними показниками: –36a–17; 7a–4b10.
4) Записати в десятковому вигляді число: 7,01 107; 2,41 10–5.
2. 1) Подати у вигляді степеня з основою
10 число:
.
2) Спростити вираз:
а) 0,9a10c–6 3a–4c–3; б) x–5 16(x–3)–4.
3. 1) Спростити:
а)
–0,9x6y–11 (–3x–4y–4);
б)
.
2) Перетворити у раціональний дріб вираз a–5 – a–3.
3) Записати у стандартному вигляді число: 613000000; 0,00000574.
Достатній рівень
1. 1) Знайти значення виразу:
а)
;
б)
.
2) Спростити
вираз
.
3) Подати у вигляді раціонального дробу вираз (a–2 + a–1 + 1) (a–2 + a).
4) Записати у стандартному вигляді число: 835,2 1014; 0,00432 10–5.
2. Знайти значення виразу .
3. Обчислити суму 2,7 · 10–4 + 3,8 10–5 і записати її у стандартному вигляді.
Високий рівень
1. 1) Обчислити
.
2) Спростити
.
3) Записати у стандартному вигляді число 4000–4.
2. Спростити вираз
.
3. Спростити вираз
.
Тематичне оцінювання навчальних досягнень учнів
Контрольна робота №3
№ 87. Варіант 1.
Середній рівень
1. 1) Обчислити:
а)
;
б)
.
2) Подати у вигляді степеня:
а)
;
б) a–6 a8;
в)
;
г) (x–2) : x–5.
3) Подати у вигляді дробу: b–10; ac–6.
4) Розв’язати рівняння:
а)
;
б)
.
2. Спростити вираз (a–4)3 5a14.
3. 1) Записати у стандартному вигляді число: 470000000; 0,000571.
2) Розв’язати задачу за допомогою рівняння.
Знайти дріб, що дорівнює
і у якого сума чисельника і знаменника
дорівнює 72.