4.2. Степінь дробу
№43. Варіант 1.
1. 1) Щоб піднести раціональний дріб до степеня, потрібно піднести до цього степеня …
а) чисельник, не змінюючи знаменник; б) знаменник, не змінюючи чисельник; в) чисельник і знаменник.
2) Якщо
— раціональний дріб, то
дорівнює…
а)
; б)
; в)
.
3) 
а)
; б)
; в)
.
2. Вказати дріб, тотожно рівний степеню (1–6):
1) 
а)
; б)
; в)
.
2) 
а)
; б)
; в)
.
3) 
а
*6 А.
Капіносов. Дид. Матеріали. Алгебра, 8
кл. Ч. І.
; б)
; в)
.
4) 
а)
; б)
; в)
.
5) 
а)
; б)
; в)
.
6) 
а)
; б)
; в)
.
3. Подати у вигляді раціонального дробу (1–6):
1)
; 2)
; 3)
;
4)
; 5)
; 6)
.
№44. Варіант 2.
1. 1) Степінь раціонального дробу тотожно дорівнює дробу, чисельник якого дорівнює _______________, а знаменник _________________.
2) 
а)
; б)
; в)
.
3) Щоб піднести дріб до степеня, потрібно записати дріб, чисельник якого дорівнює ______________, а знаменник __________________.
2. Вказати дріб, тотожно рівний степеню (1–6):
1) 
а)
; б)
; в)
.
2) 
а)
; б)
; в)
.
3) 
а)
; б)
; в)
.
4) 
а)
; б)
; в)
.
5) 
а)
; б)
; в)
.
6) 
а)
; б)
; в)
.
3. Подати у вигляді раціонального дробу (1–6):
1)
; 2)
; 3)
;
4)
; 5)
; 6)
.
4.3. Ділення дробів
№45. Варіант 1.
1. 1) Для раціонального
дробу
оберненим є дріб…
а)
; б)
; в)
.
2) Якщо
і
— раціональні дроби, то
дорівнює…
а)
; б)
; в)
.
3) 
а)
; б)
; в)
.
4) 
а)
; б)
.
5) 
а)
; б)
.
2. Вказати вираз, тотожно рівний частці (1–8):
1) 
а)
; б)
; в)
.
2) 
а)
; б)
3; в)
.
3) 
а)
; б)
; в)
.
4) 
а)
; б)
5а; в)
.
5) 
а)
; б)
; в)
.
6) 
а)
; б)
; в)
а12.
7) 
а)
; б)
; в)
2.
8) 
а)
; б)
; в)
.
3. Виконати ділення (1–8):
1)
; 2)
;
3)
; 4)
;
5)
; 6)
;
7)
; 8)
.
№46. Варіант 2.
1. 1) Частка двох раціональних дробів тотожно дорівнює добутку діленого і дробу, ______________________ до дільника.
2) 
а)
; б)
; в)
.
3) Щоб поділити один дріб на інший, потрібно перший дріб помножити на дріб, _____________ до другого.
4) Щоб поділити цілий раціональний вираз на раціональний дріб або, навпаки, дріб на цілий вираз, потрібно подати вираз у вигляді дробу зі знаменником ___________ і виконати дію за правилом ділення раціональних дробів.
5) 
а)
; б)
; в)
.
6) 
а)
; б)
; в)
.
2. Вказати вираз, тотожно рівний частці (1–8):
1) 
а)
; б)
; в)
5ху.
2) 
а)
; б)
5; в)
.
3) 
а)
m + n; б)
; в)
.
4) 
а)
7a; б)
; в)
.
5) 
а)
; б)
; в)
4(a + 1).
6) 
а)
; б)
a20; в) а9.
7) 
а)
; б)
4; в)
.
8) 
а) ; б) ; в) 10.
3. Виконати ділення (1–8):
1)
; 2)
;
3)
; 4)
;
5)
; 6)
;
7)
; 8)
.
Відтворення і застосування теорії
Самостійні роботи
№47. Варіант 1.
Середній рівень
Подати у вигляді дробу:
1. 1)
; 2)
; 3)
; 4)
.
2. 1)
; 2)
; 3)
; 4)
.
3. 1)
; 2)
;
3)
; 4)
.
Достатній рівень
Подати у вигляді дробу:
1. 1)
; 2)
.
2. 1)
; 2)
.
3. Подати дріб
у вигляді раціонального дробу.
Високий рівень
1. Виконати дії:
1)
; 2)
.
2. Подати у вигляді раціонального дробу:
1)
; 2)
.
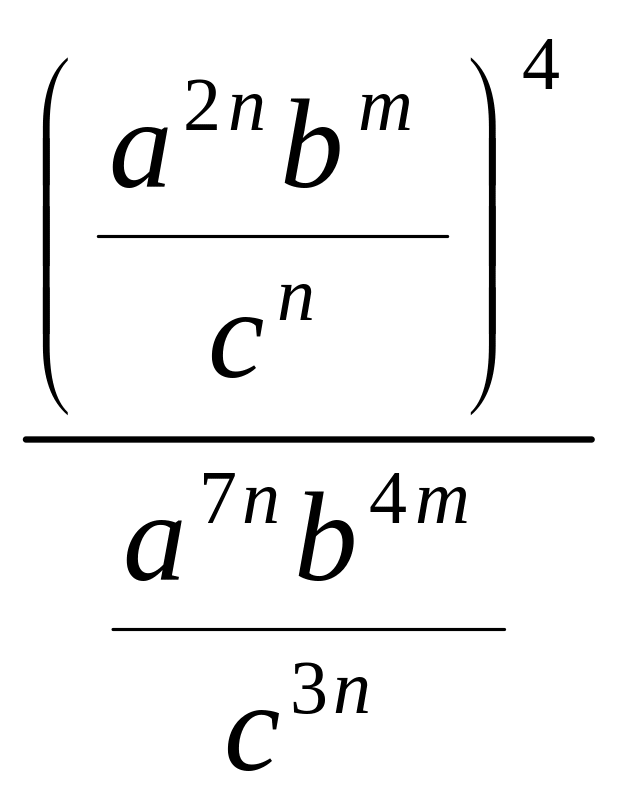3. Довести тотожність
.
№48. Варіант 2.
Середній рівень
Подати у вигляді дробу:
1. 1)
; 2)
; 3)
; 4)
.
2. 1)
; 2)
; 3)
; 4)
.
3. 1)
; 2)
;
3)
; 4)
.
Достатній рівень
Подати у вигляді дробу:
1. 1)
; 2)
.
2. 1)
; 2)
.
3. Подати дріб
у вигляді раціонального дробу.
Високий рівень
1. Виконати дії:
1)
;
2)
.
2. Подати у вигляді раціонального дробу:
1)
; 2)
.
3. Довести тотожність
.
№49. Варіант 3.
Середній рівень
Подати у вигляді дробу:
1. 1)
; 2)
; 3)
; 4)
.
2. 1)
; 2)
; 3)
; 4)
.
3. 1)
; 2)
;
3)
; 4)
.
Достатній рівень
Подати у вигляді дробу:
1. 1) 
; 2)
.
2. 1) 
;
2) 
.
3. Подати дріб
у вигляді раціонального дробу.
Високий рівень
1. Подати у вигляді раціонального дробу:
1) 
;
2) 
.
2. Подати у вигляді раціонального дробу:
1)
; 2)
.
3. Довести тотожність
.
№50. Варіант 4.
Середній рівень
Подати у вигляді дробу:
1. 1)
; 2)
; 3)
; 4)
.
2. 1)
; 2)
; 3)
; 4)
.
3. 1)
; 2)
;
3)
; 4)
.
Достатній рівень
Подати у вигляді дробу:
1. 1)
; 2)
.
2. 1) 
; 2)
.
3. Подати дріб
у вигляді раціонального дробу.
Високий рівень
1. Виконати дії:
1) 
; 2)
.
2. Подати у вигляді раціонального дробу:
1) 
; 2)
.
3. Довести тотожність:
.
№51. Варіант 5.
Середній рівень
Подати у вигляді дробу:
1. 1) 
; 2)
;
3) 
; 4)
.
2. 1) 
; 2)
;
3)
; 4)
.
3. 1)
; 2)
;
3)
; 4)
.
Достатній рівень
1. Виконати дії:
1)
; 2)
.
2. Подати у вигляді дробу:
1)
; 2)
.
3. Подати дріб
у вигляді раціонального дробу.
Високий рівень
1. Виконати дії:
:
.
2. Подати у вигляді раціонального дробу:
1) 
; 2)
.
3. Довести тотожність
.
№52. Варіант 6.
Середній рівень
Подати у вигляді дробу:
1. 1) 
; 2)
;
3) 
; 4)
.
2. 1) 
; 2)
;
3) 
; 4)
.
3. 1) 
; 2)
;
3) 
; 4)
.
Достатній рівень
1. Виконати дії:
1)
; 2)
.
2. Подати у вигляді дробу:
1)
; 2)
.
3. Подати дріб
у вигляді раціонального дробу.
Високий рівень
1. Виконати дії
.
2. Подати у вигляді раціонального дробу:
1) 
; 2)
.
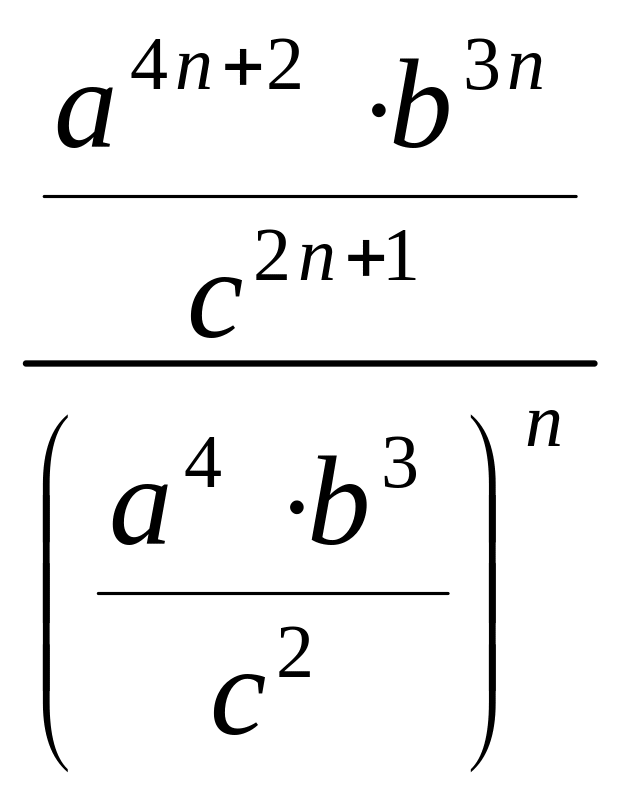3. Довести тотожність:
.
ТЕМА 5. ТОТОЖНІ ПЕРЕТВОРЕННЯ РАЦІОНАЛЬНИХ ВИРАЗІВ НА ОСНОВІ ПРАВИЛ АРИФМЕТИЧНИХ ДІЙ
Початкове вивчення теорії
Навчальні завдання
№53. Варіант 1.
1. 1) У який найпростіший вираз може бути перетворений будь-який раціональний вираз у результаті послідовного виконання дій?
а) У многочлен стандартного вигляду; б) у раціональний дріб, у якого чисельник і знаменник — многочлени стандартного вигляду.
Вказати арифметичні дії (2–4):
2) першого ступеня; 3) другого ступеня; 4) третього ступеня.
а) Піднесення до степеня з натуральним показником; б) множення і ділення; в) додавання і віднімання.
5) Вказати послідовність виконання дій у виразі, що не містить дужок.
а) Спочатку виконують дії першого ступеня (додавання і віднімання), потім — другого ступеня (множення і ділення) і, нарешті, — третього ступеня (піднесення до степеня); б) спочатку дії третього ступеня, якщо вони є; далі другого ступеня (множення і ділення), і, нарешті, — першого ступеня (додавання і віднімання).
6) У якій послідовності виконують дії одного ступеня?
а) У послідовності їх запису (зліва направо); б) у порядку, зворотному до їх запису — справа наліво.
7) Назвати математичний знак, який застосовують для зміни послідовності виконання дій.
2. Назвати дію, яку виконують першою, перетворюючи вираз (1–4):
1)
; 2)
;
3)
; 4)
.
3. Скласти раціональний вираз, що містить дві дії, які виконують у такій послідовності (1–4):
1) додавання; множення; 2) віднімання; ділення; 3) множення; віднімання; 4) ділення; додавання.
№54. Варіант 2.
Доповнити запис (1–6).
1. 1) Будь-який раціональний вираз у результаті послідовного виконання дій може бути перетворений у раціональний дріб, у якого чисельник і знаменник _________________________________________.
2) Діями першого ступеня називають дії __________________________.
3) Діями другого ступеня називають дії __________________________.
4) Дією третього ступеня називають дію __________________________.
5) Якщо раціональний вираз не містить дужок, то спочатку виконують дії _____________________________.
6) Дії з виразами одного ступеня виконують у порядку їх ___________.
2. Назвати дію, яку виконують першою, перетворюючи вираз (1–4):
1) 
; 2)
;
3) 
; 4)
.
3. Скласти раціональний вираз, що містить дві дії, які виконують у такій послідовності (1–4):
1) додавання; ділення; 2) віднімання; множення; 4) множення; додавання; 4) ділення; віднімання.
Відтворення і застосування теорії
Самостійні роботи
№55. Варіант 1.
Середній рівень
Виконати дії:
1. 1) 
; 2)
.
2. 
.
3. 
.
Достатній рівень
Виконати дії:
1. 1) 
; 2)
.
2. 
.
3. Подати дріб
у вигляді раціонального дробу.
Високий рівень
Виконати дії:
1. 1) 
;
2) 
.
2. 
.
3. Подати вираз
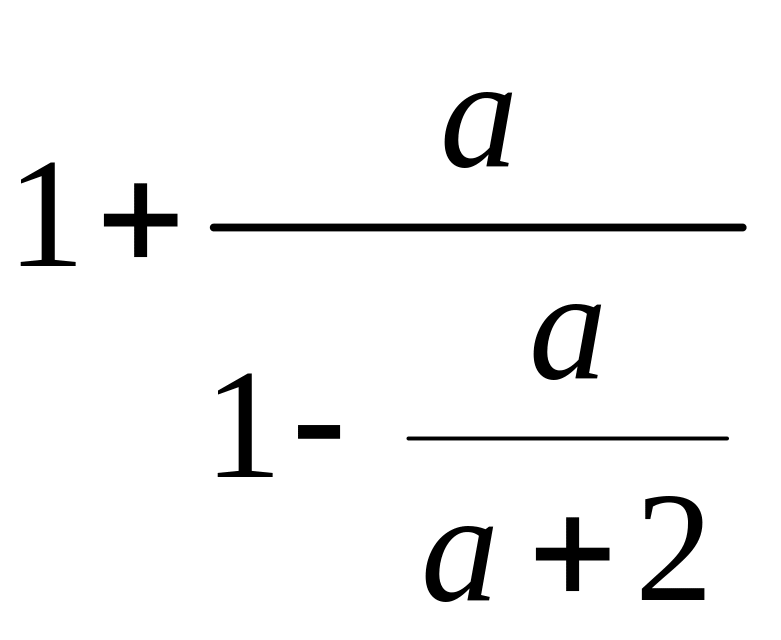у вигляді раціонального дробу.
№56. Варіант 2.
Середній рівень
Виконати дії:
1. 1) 
; 2)
.
2. 
.
3
*7
А. Капіносов.
Дид. Матеріали. Алгебра, 8 кл. Ч. І.
.
Достатній рівень
Виконати дії:
1. 1) 
; 2) 
.
2. 
.
3. Подати вираз
у вигляді раціонального дробу.
Високий рівень
Виконати дії:
1. 1) 
;
2) 
;
2. 
.
3. Подати вираз
у вигляді раціонального дробу.
№57. Варіант 3.
Середній рівень
Виконати дії:
1. 1) 
; 2)
.
2. 
.
3. 
.
Достатній рівень
Виконати дії:
1. 1) 
; 2) 
.
2. 
.
3. Подати дріб
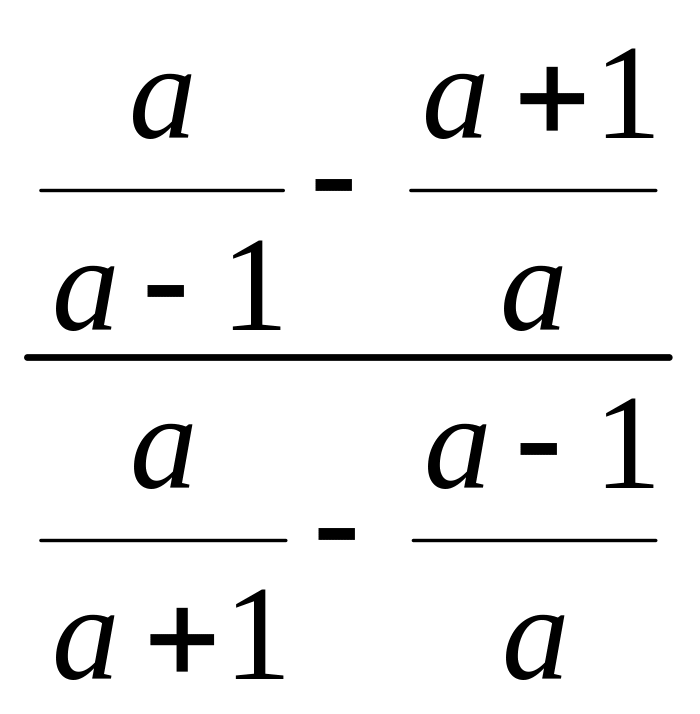у вигляді раціонального дробу.
Високий рівень
Виконати дії:
1. 1) 
;
2) 
.
2. 
.
3. Подати вираз
у вигляді раціонального дробу.
№58. Варіант 4.
Середній рівень
Виконати дії:
1. 1) 
; 2)
.
2. 
.
3. 
.
Достатній рівень
Виконати дії:
1. 1) 
; 2)
.
2. 
.
3. Подати вираз
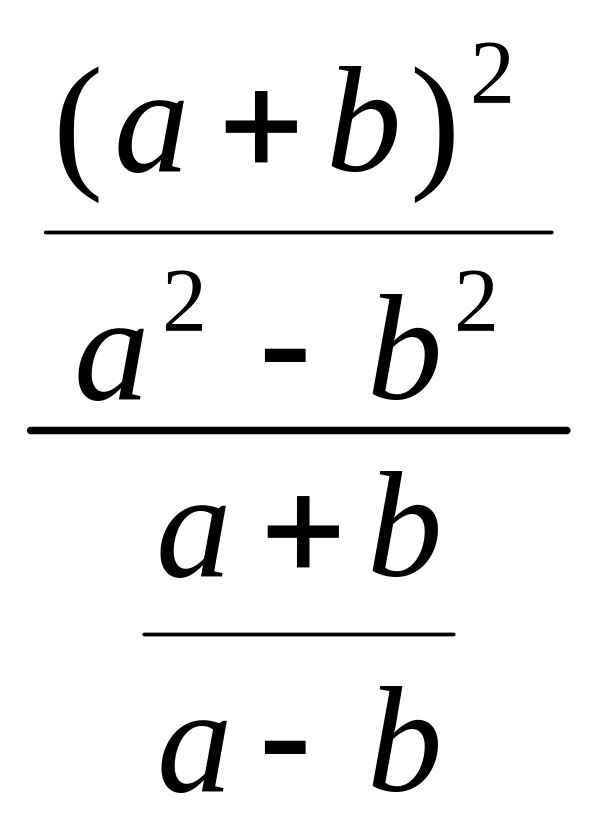у вигляді раціонального дробу.
Високий рівень
Виконати дії:
1. 1) 
;
2) 
.
2. 
.
3. Подати вираз
у вигляді раціонального дробу.
№59. Варіант 5.
Середній рівень
Виконати дії:
1. 1) 
; 2)
.
2. 
.
3. 
.
Достатній рівень
Виконати дії:
1. 1)
; 2)
.
2. 
.
3. Подати дріб
у вигляді раціонального дробу.
Високий рівень
Виконати дії:
1. 1) 
;
2) 
.
2. 
.
3. Подати вираз
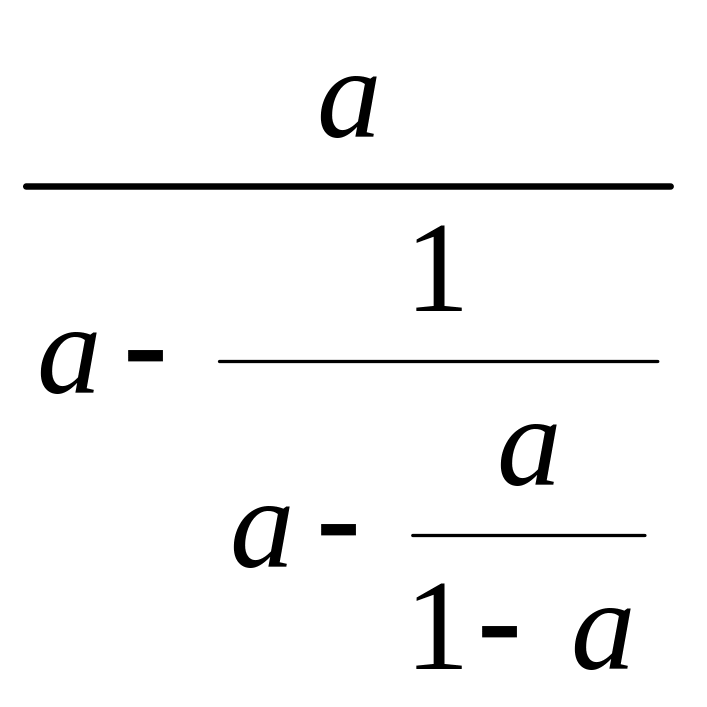у вигляді раціонального дробу.
№60. Варіант 6.
Середній рівень
Виконати дії:
1. 1) 
; 2)
.
2. 
.
3. 
.
Достатній рівень
Виконати дії:
1. 1) 
; 2)
.
2. 
.
3. Подати вираз
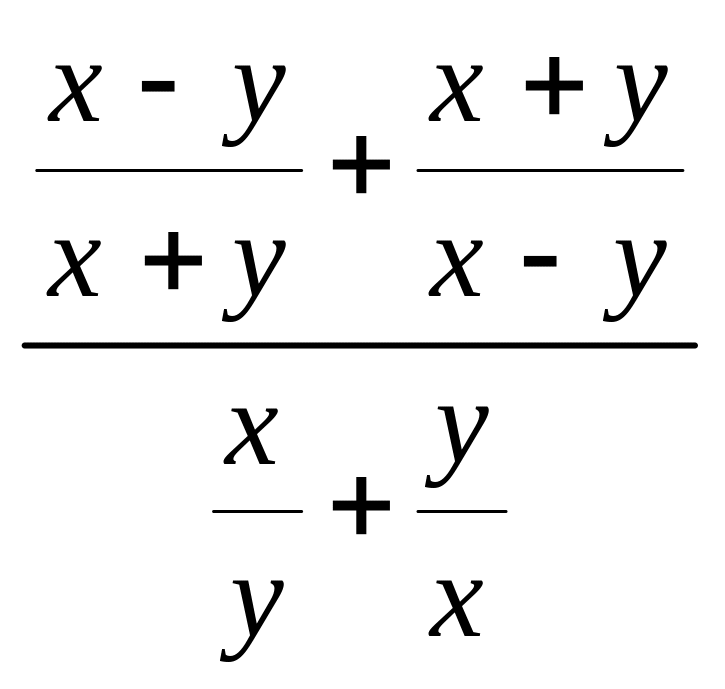у вигляді раціонального дробу.
Високий рівень
Виконати дії:
1. 1) 
;
2) 
.
2. 
.
3. Подати вираз
у вигляді раціонального дробу.
Тематичне оцінювання навчальних досягнень учнів
Контрольна робота №2
№61. Варіант 1.
Середній рівень
Подати у вигляді раціонального дробу:
1. 1) 
; 2)
; 3)
.
2. 1)
; 2)
.
3. 
.
Достатній рівень
Подати у вигляді раціонального дробу:
1. 1)
; 2)
.
2. 
.
3. 
.
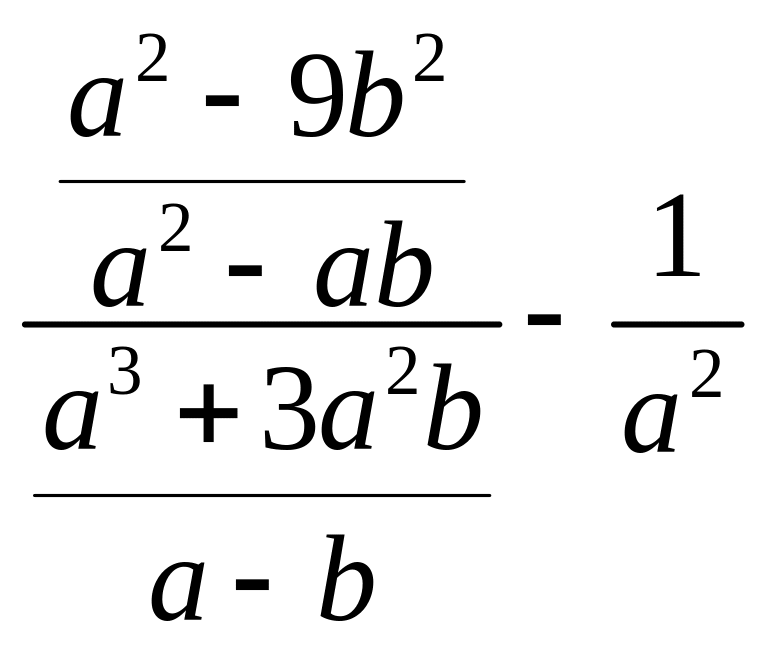Високий рівень
Подати у вигляді раціонального дробу:
1. 1) 
;
2) 
.
2. 
.
3. 
.
№62. Варіант 2.
Середній рівень
Подати у вигляді раціонального дробу:
1. 1)
; 2)
; 3)
.
2. 1)
; 2)
.
3. 
.
Достатній рівень
Подати у вигляді раціонального дробу:
1. 1) 
; 2)
.
2. 
.
3. 
.
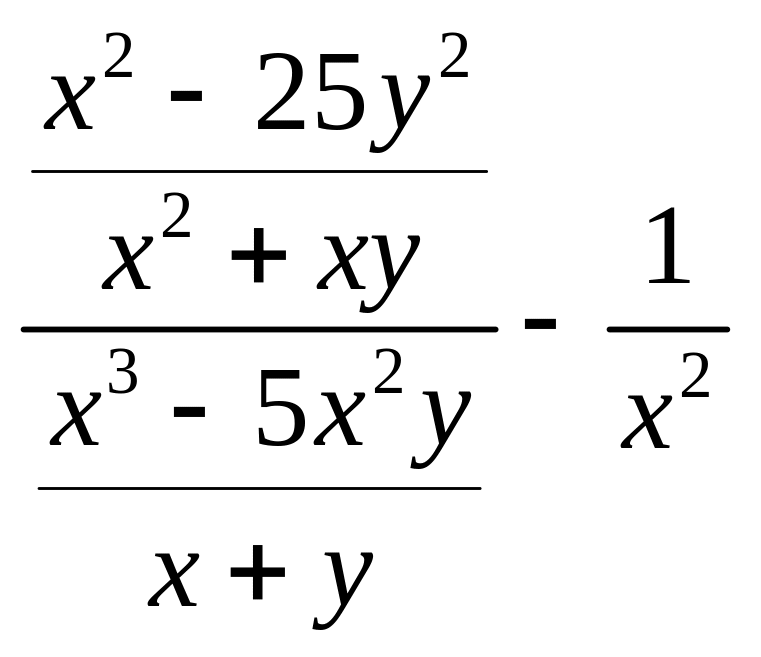Високий рівень
Подати у вигляді раціонального дробу:
1. 1) 
;
2) 
.
2. 
.
3. 
.
№63. Варіант 3.
Середній рівень
Подати у вигляді раціонального дробу:
1. 1) 
; 2)
; 3)
.
2. 1)
; 2)
.
3. 
.
Достатній рівень
Подати у вигляді раціонального дробу:
1. 1) 
;
2)
.
2. 
.
3. 
.
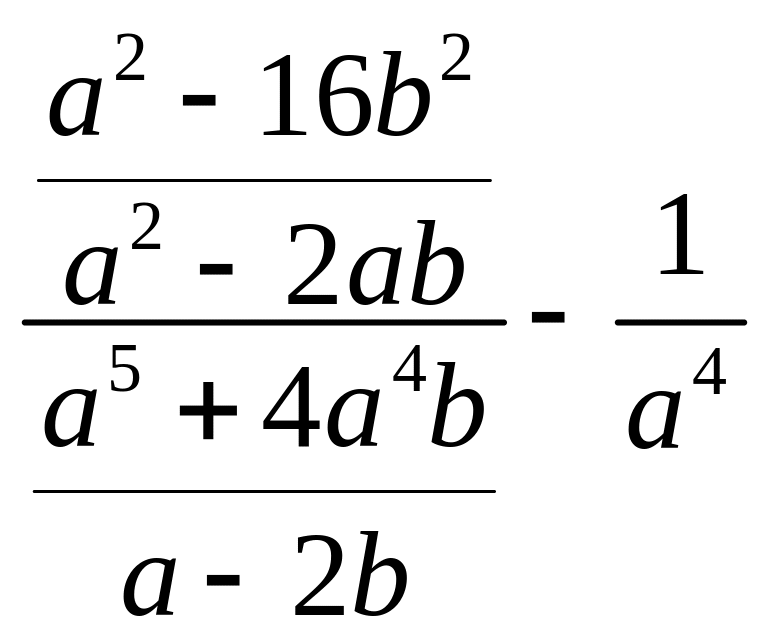Високий рівень
Подати у вигляді раціонального дробу:
1. 1) 
;
2) 
.
2. 
.
3. 
.
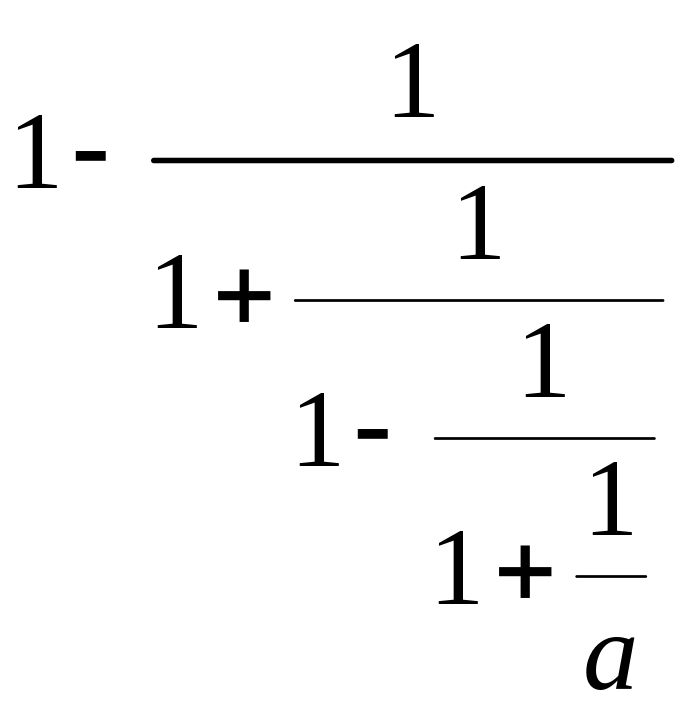№64. Варіант 4.
Середній рівень
Подати у вигляді раціонального дробу:
1. 1) 
; 2)
; 3)
.
2. 1) 
; 2)
.
3. 
.
Достатній рівень
Подати у вигляді раціонального дробу:
1. 1) 
; 2)
.
2. 
.
3. 
.
Високий рівень
Подати у вигляді раціонального дробу:
1. 1) 
;
2) 
.
2. 
.
3. 
.
ТЕМА 6. ДРОБОВІ РАЦІОНАЛЬНІ РІВНЯННЯ
Поняття дробового раціонального рівняння
Найпростіші дробові раціональні рівняння
Початкове вивчення теорії
Навчальні завдання
6.1. Поняття дробового раціонального рівняння
№65. Варіант 1.
1. 1) Як називають рівняння, у яких обидві частини є виразами, що не містять інших дій, крім арифметичних і піднесення до степеня з натуральним показником?
Як називають раціональні рівняння, у яких (2–4):
2) обидві частини не містять ділення на вираз зі змінними;
3) хоча б в одну з його частин входить ділення на вираз зі змінною?
4) Як називають множину усіх чисел, за яких мають смисл обидві частини рівняння з однією змінною?
а) Областю рівняння; б) область допустимих значень змінної у рівнянні або областю визначення рівняння;
5) Як називають число, за якого рівняння з однією змінною перетворюється у правильну числову рівність?
6) Чи може корінь рівняння не входити в область допустимих значень рівняння?
Серед наведених перетворень рівнянь а)–е) вказати (7–8):
7) три, що не приводять до зміни області допустимих значень змінної у рівнянні;
8) три, що можуть приводити до розширення області допустимих значень змінної у рівнянні:
а) перенесення доданка з однієї частини в іншу зі зміною знака;
б) множення обох частин на число, відмінне від нуля;
в) множення обох частин рівняння на вираз зі змінною;
г) ділення обох частин рівняння на число, відмінне від нуля;
д) скорочення дробів, які входять у рівняння, на вираз зі змінною;
е) зведення подібних доданків, які є дробами.
9) Які з коренів цілого рівняння, утвореного із дробового, є коренями і дробового рівняння?
а) Тільки ті, що входять в область допустимих значень дробового рівняння; б) усі корені цілого рівняння.
10) Який завершальний етап розв’язування дробових раціональних рівнянь після знаходження коренів цілого рівняння?
а) Запис усіх коренів цілого рівняння як коренів дробового рівняння; б) відбір коренів цілого рівняння, що входять в область допустимих значень даного дробового рівняння (перевірка коренів).
2. Серед наведених рівнянь а)–е) вказати три, що є (1–2):
1) цілими раціональними рівняннями;
2) дробовими раціональними рівняннями:
а)
; б)
х2 + 9x = 0; в)
;
г)
; д)
; е)
.
Вказати область допустимих значень дробового раціонального рівняння (3–5):
3) 
:
а) усі числа; б) усі числа, крім 1 і 0; в) усі числа, крім 1.
4) 
:
а) усі числа, крім 1; б) усі числа, крім 2; в) усі числа, крім 1 і 2.
5) 
:
а) усі числа; б) усі числа, крім 2; в) усі числа, крім 0.
6) Вказати, яке з чисел а)–в) є коренем
дробового рівняння
:
а) 0; б) 4; в) –6.
Вказати ціле рівняння, що утвориться із даного рівняння (7–9):
7) 
,
якщо звести подібні члени:
а) 5x = 13; б) 5x + 13 = 0.
8) 
,
якщо скоротити дріб:
а) x + 4 + х = 12; б) x – 4 + х= 12.
9) 
,
якщо помножити обидві частини рівняння
на вираз х – 2:
а) x – 2 = 51; б) 17(x – 2) = 0; в) 17(x – 2) = 3.
Вказати вираз, при множенні на який обох частин дробового рівняння воно перетворюється у ціле (10–12):
10) 
:
а) 5х; б) х + 4; в) х + 4 + 5х.
11) 
:
а) х(x – 3); б) х; в) х – 3.
12) 
:
а) х – 2; б) х2 – 4; в) х + 2.
3. Записати (1–2):
1) три цілі рівняння з однією змінною;
2) три дробові рівняння з однією змінною.
Знайти область допустимих значень рівняння (3–6):
3) 
; 4)
;
5) 
;
6)
.
Записати ціле рівняння, що утвориться з рівняння (7–8):
7) 
,
якщо скоротити дріб на х + 4;
8) 
,
якщо помножити обидві його частини на
х.
№66. Варіант 2.
1 Доповнити записи (1–12).
1) Раціональними рівняннями називають рівняння, у яких обидві частини є ______________ виразами, тобто не містять інших дій, крім _______________________________________.
2) Цілими рівняннями називають раціональні рівняння, у яких обидві частини є ____________ виразами, тобто раціональними виразами, що не містять _______________________________________.
3) Дробовими рівняннями називають рівняння, у яких хоча б одна частина є __________ виразом, тобто містить ділення на _____________.
4) Множину всіх дійсних чисел, за яких мають зміст обидві частини рівняння, називають ______________________________________, або _______________________ рівняння.
5) Областю допустимих значень будь-якого цілого рівняння є множина _________________________________.
6) Областю допустимих значень дробового рівняння з однією змінною є усі числа, крім тих, за яких отримують ділення на число _________________.
7) Число, за якого рівняння з однією змінною перетворюється у правильну числову рівність, називають _________________.
8) Число, яке не входить до області допустимих значень рівняння, не може бути його _________________.
9) Основним методом розв’язування дробових раціональних рівнянь є їх зведення до _________________________________.
10) Після перенесення доданків з однієї частини рівняння в іншу зі зміною знака, множення або ділення обох частин рівняння на ______________, область допустимих значень рівнянь не змінюється.
11) Коренями дробового рівняння, утвореного з нього цілого рівняння, можуть бути тільки ті корені, що входять до області ______________.
2. Серед наведених рівнянь а)–е) вказати три, що є (1–2):
1) цілими раціональними рівняннями;
2) дробовими раціональними рівняннями:
а)
; б)
х2 – 4x = 0; в)
;
г)
; д)
; е)
.
Вказати область допустимих значень дробового раціонального рівняння (3–5):
3) 
:
а) усі числа; б) усі числа, крім 7 і 0; в) усі числа, крім 7.
4) 
:
а) усі числа, крім 6; б) усі числа, крім 2; в) усі числа, крім 2 і 6.
5) 
:
а) усі числа; б) усі числа, крім 0.
6) Вказати, яке з чисел а)–в) є коренем
дробового рівняння
:
а) 0; б) 2; в) 1.
Вказати ціле рівняння, що утвориться з рівняння (7–9):
7) 
після зведення подібних членів:
а) 14x = –7; б) 14x = 7.
8) 
після скорочення дробу:
а) x + 3 + 5х = 21; б) x – 3 + 5х= 21.
9) 
після множення обох частин рівняння на
вираз x – 3:
а) 2(x – 3) = 1; б) x – 3 = 10; в) 2(x – 3) = 5.
Вказати вираз, при множенні на який обох частин дробового рівняння воно перетворюється у ціле (10–12):
10)
:
а) 7х; б) х – 3; в) (х – 3) 7х.
11)
:
а) х(x + 2); б) х + 2; в) х.
12)
:
а) х – 5; б) х + 5; в) х2 – 25.
3. Записати (1–2):
1) три цілі рівняння з двома змінними;
2) три дробові рівняння з двома змінними.
Знайти область допустимих значень змінної рівняння (3–6):
3)
; 4)
;
5)
; 6)
.
Записати ціле рівняння, що утвориться з рівняння (7–8):
7) 
після скорочення дробу на х – 5;
8) 
після множення обох його частин на х.