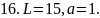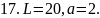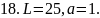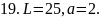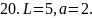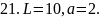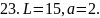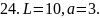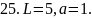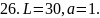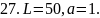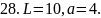4.2. Вычисление работы переменной силы

Пусть некоторое тело движется по прямой l под действием переменной силы 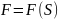. Работа этой силы на участке пути вычисляется по формуле

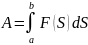(2)

Пример 2.

Вычислить работу, которую необходимо затратить, чтобы растянуть пружину на 20 см, если известно, что для удлинения её на 1 см нужно приложить силу в 1 кН.

Решение:

Согласно закону Гука, сила 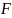растяжения пружины пропорциональна её растяжению, т.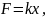е. где 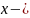растяжение пружины (в метрах), 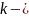коэффициент пропорциональности.

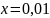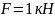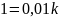Т.к. по условию при м сила , то из равенства получаем . Следовательно, искомая работа

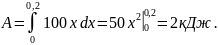
4.3. Вычисление силы давления жидкости на пластину

Решение данной задачи покажем на примере.

П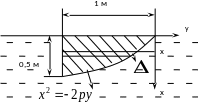 ример 3.

Вычислить силу давления воды на пластину, вертикально погруженную в воду, считая что удельный вес воды равен 9,81 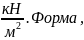размеры и расположение пластины указаны на рисунке.

Решение.

Задаём систему координат относительно пластины.

Простейшее уравнение параболы в данном случае имеет вид 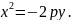Т.к. парабола проходит через т. А(0,5;-1), то находим p:

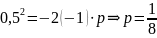т.е. уравнение параболы

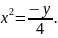
Выделим на глубине горизонтальную полоску шириной 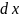и площадью . Давление воды на эту полоску

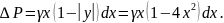
Тогда давление воды на всю пластину

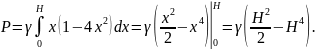
При Н=0,5м и 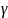=9,81 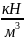получаем:

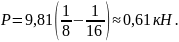
4.4. Вычисление координат центра масс плоской фигуры

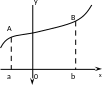1. К оординаты центра масс плоской линии.

Рассмотрим дугу АВ графика функции имеющую линейную плотность 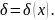Координаты центра масс С(x_c, y_c) такой дуги вычисляются по формулам:

,

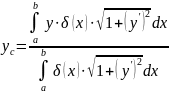(4)

2. Координаты центра масс плоской фигуры.

Р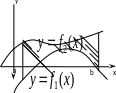 ассмотрим фигуру, ограниченную снизу линией сверху - 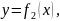т.е. 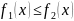на отрезке поверхностная плотность фигуры Центр масс такой фигуры вычисляется по формулам

,

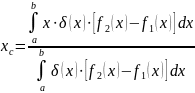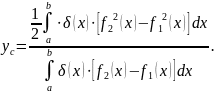
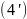
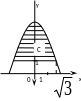
Пример 4.

Найти координаты центра масс однородной фигуры, ограниченной линиями

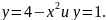
Решение.

Из симметричности и однородности этой фигуры очевидно, что 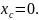Определим 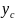по формуле

.

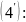
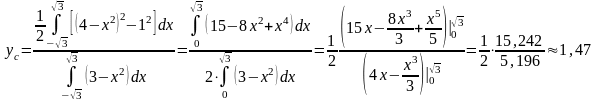Задание 13.

Варианты 1-15.

Материальная точка движения по прямой со скоростью Найти путь S, пройденный этой точкой за промежуток времени

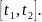
1.

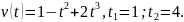
2.

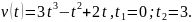
3.

4.

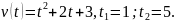
5.

6.

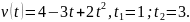
7.

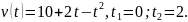
8.

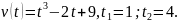
9.

10.

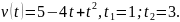
11.

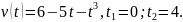
12 .

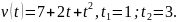
13.

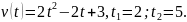
14.

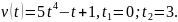
15.

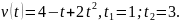
Варианты 16-30.

Вычислить работу, которую нужно затратить, чтобы растянуть пружину на L см, если известно, что для удлинения её на 1 см необходимо приложить силу в а кН.

Задание 14.

Вычислить силу давления вводы на пластину, вертикально погруженную в воду, считая, что удельный вес воды равен 9,81 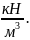Форма, размеры и расположение пластины указаны на рисунке.

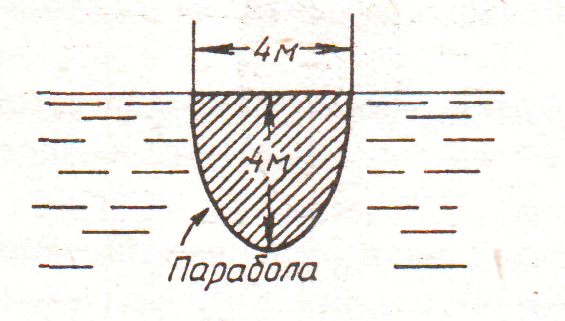
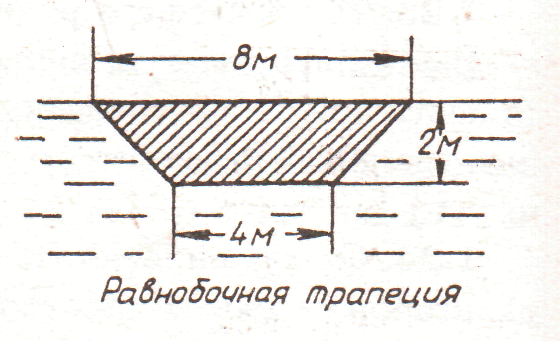
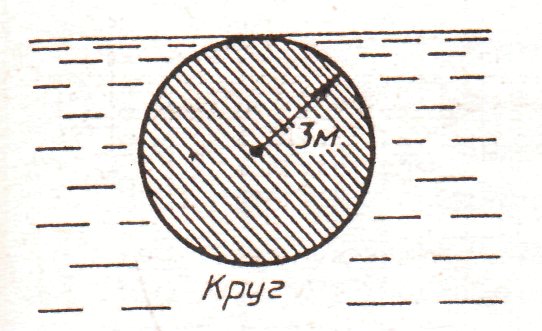
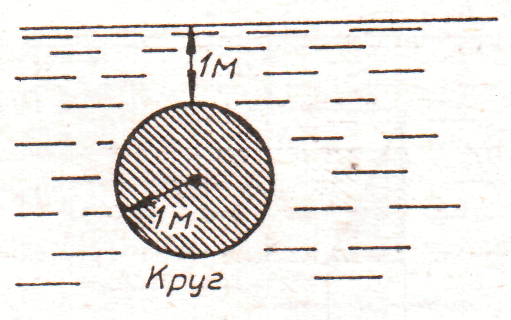
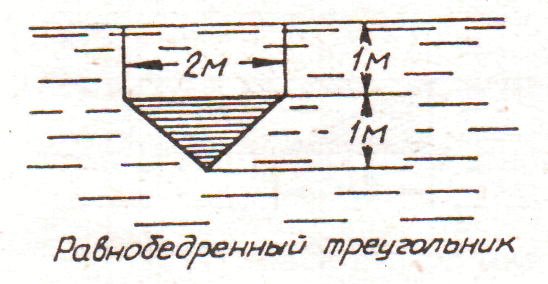
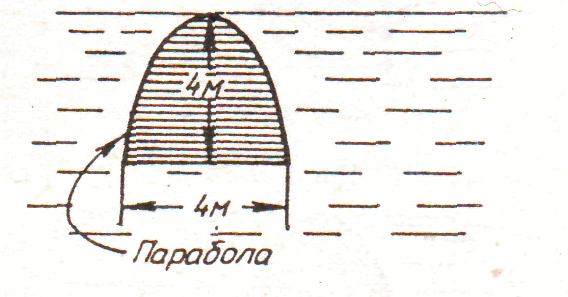
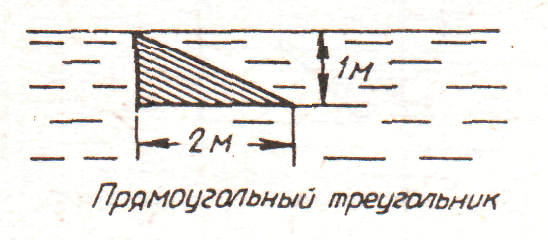
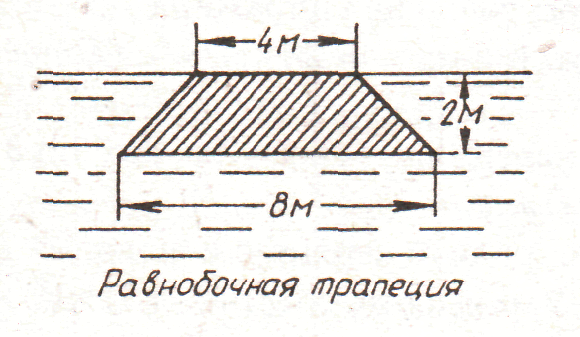
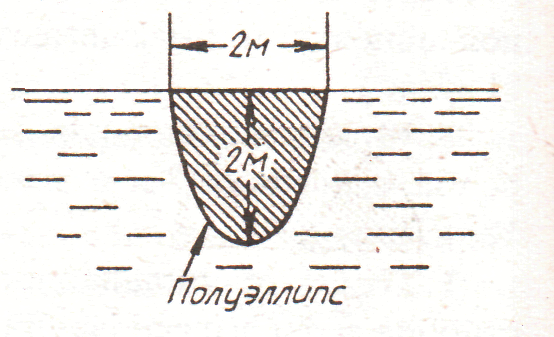
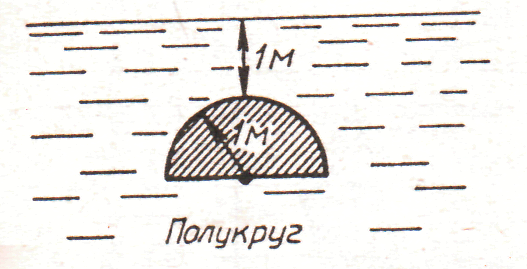
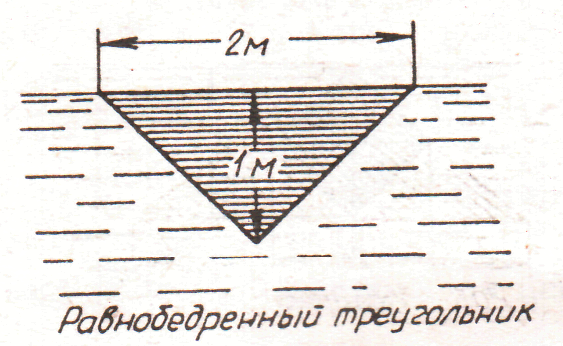
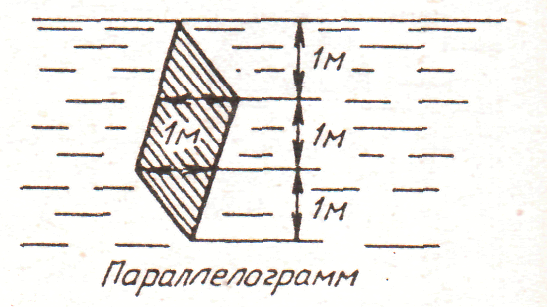
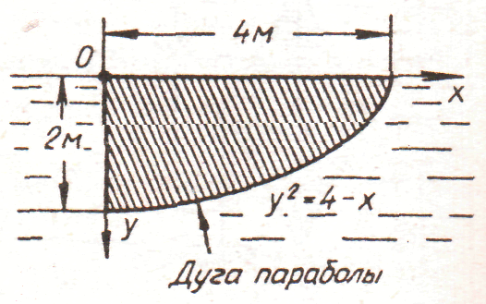
1. рис. 1.	2. рис. 2.
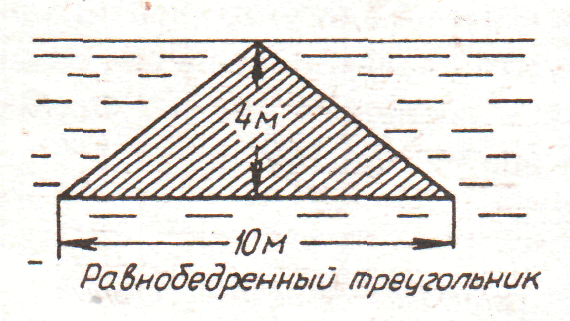
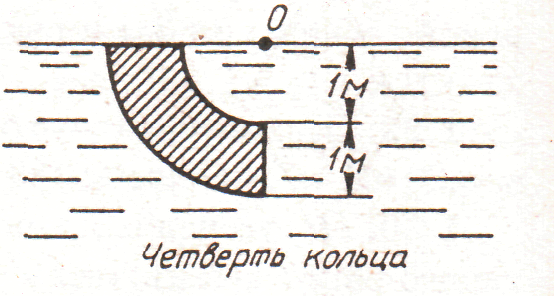
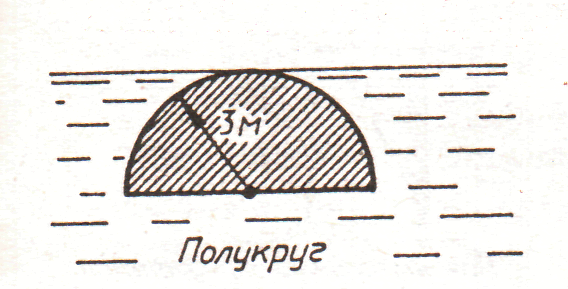
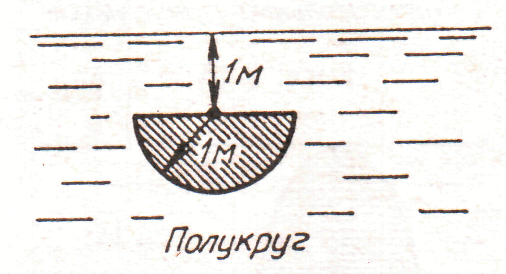
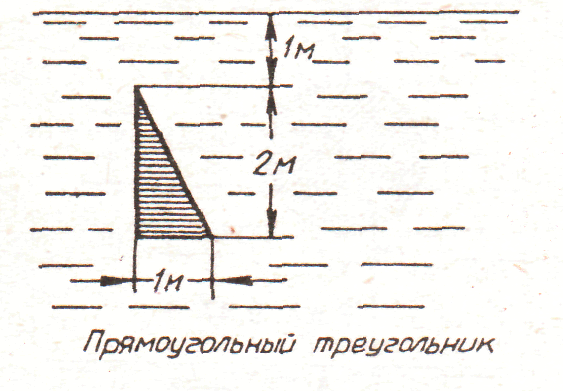
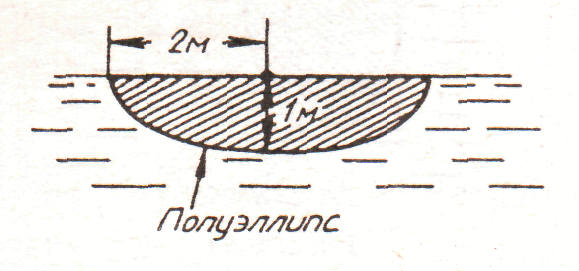
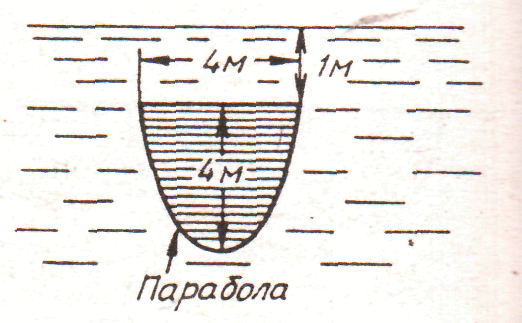
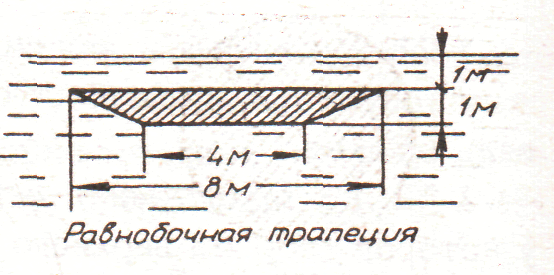
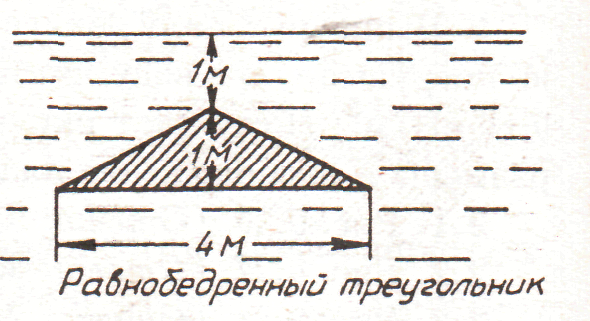
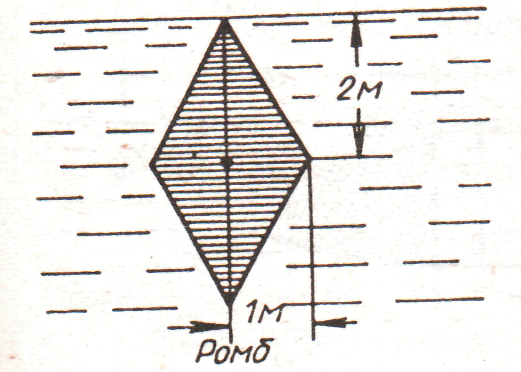
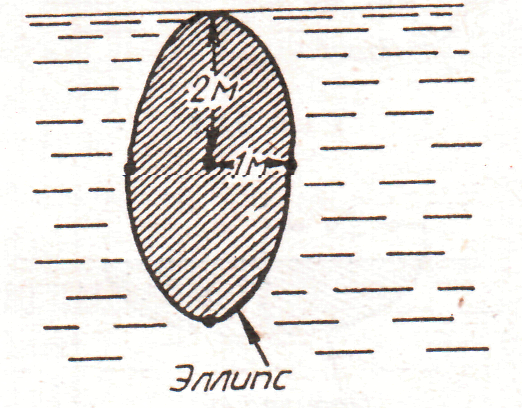
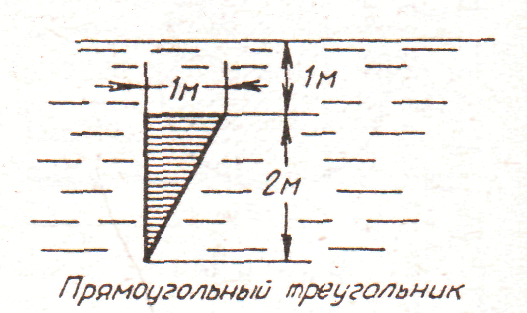
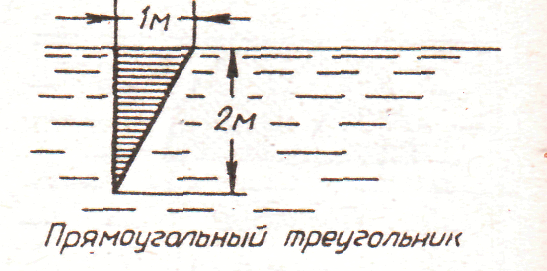
3. рис. 3.	4. рис. 4.
5. рис. 5.	6. рис. 6.
7. рис. 7.	8. рис. 8.
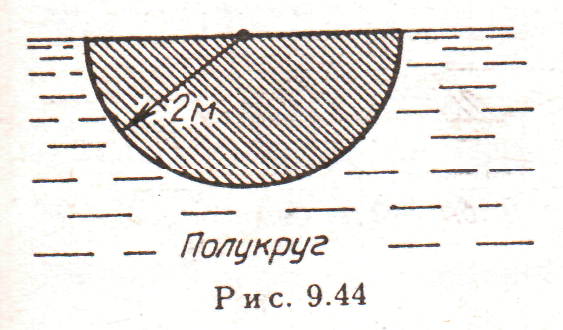
9. рис. 9.	10. рис. 10.
11. рис. 11.	12. рис. 12.
13. рис. 13.	14. рис. 14.
15. рис. 15.	16. рис. 16.
17. рис. 17.	18. рис. 18.
19. рис. 19.	20. рис. 20.
21. рис. 21.	22. рис. 22.
23. рис. 23.	24. рис. 24.
25. рис. 25.	26. рис. 26.
27. рис. 27.	28. рис. 28.
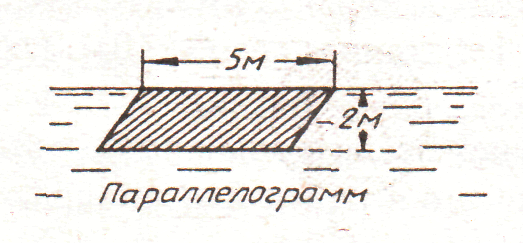
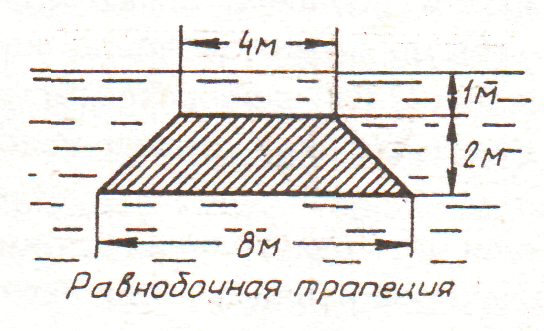
29. рис. 29.	30. рис. 30.

Задание 15.

Найти координаты центра масс однородной плоской кривой L.

1. L: полуокружность , расположенная над осью Ox.

2. L: первая арка циклоиды , .

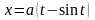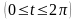3. L: дуга астроиды 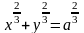, расположенная в третьем квадрате.

4. L: дуга окружности радиусом R, стягивающая центральный угол .

5. L: дуга цепной линии .

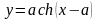
6. L: дуга кардиоиды .

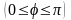7. L: дуга логарифмической спирали .

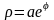
8. L: одна арка циклоиды , .

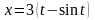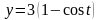9. L: дуга астроиды 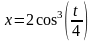, расположена в первом квадрате.

10. L: дуга кривой , .

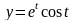
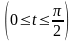11. L: дуга кардиоиды .

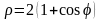12. L: кривая 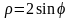от точки (0;0) до точки .

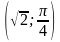13. L: дуга развертки окружности , .

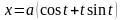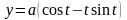
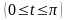14. L: кривая 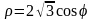, заключенная между лучами 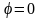и .

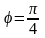15. L: кривая , .

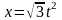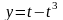
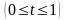Найти координаты центра масс плоской однородной фигуры Ф, ограниченной данными линиями.

16. Ф – треугольник, стороны которого лежат на прямых , , .

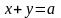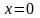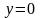17. Ф ограничена эллипсом 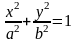и осями координат .

18. Ф ограничена первой аркой циклоиды , и осью Ох.

19. Ф ограничена кривыми , .

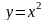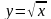20. Ф ограничена дугой синусоиды 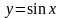и отрезком оси Ох .

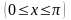21. Ф ограничена полуокружностью 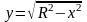и осью Ох.

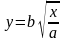
22. Ф ограничена дугой параболы , осью Ох и прямой .

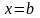23. Ф ограничена дугой параболы , осью Оyи прямой .

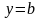24. Ф ограничена замкнутой линией .

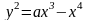25. Ф ограничена осями координат и дугой астроиды, расположенной в первом квадрате.

26. Ф – сектор круга радиусом R с центральным углом, равным 2 .

27. Ф ограничена кардиоидой .

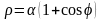28. Ф ограничена первой петлей лемнискаты Бернулли .

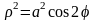29. Ф ограничена осями координат и параболой .

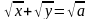30. Ф ограничена полукубической параболой 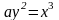и прямой .
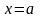
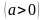