3.4. Вычисление площади поверхности вращения
а) Площадь поверхности вращения в декартовых координатах
Пусть
дуга АВ кривой
где
- непрерывно дифференцируемая функция,
вращается вокруг оси ОХ. Тогда площадь
Р полученной поверхности вращения
вычисляется по формуле :
.
(13)
Здесь a и b – абсциссы концов кривой АВ, точек А и В соответственно.
Аналогично,
если кривая задана уравнением
(c
и d
соответственно, ординаты точек С
и D
концов дуги CD),
то площадь поверхности вращения
вычисляется:
.
(13′)
Пример 13.
В
ычислить
площадь поверхности, образованной
вращением вокруг оси ОУ
дуги кривой
расположенной над осью абсцисс.
Решение.
Дуга
CD
содержится между точкой с ординатой
и
это и есть пределы интегрирования. Здесь
.
По формуле (13′) имеем:
(кв.ед.).
б) Площадь поверхности вращения в случае, когда кривая задана параметрически
Если
кривая, дуга АВ которой вращается вокруг
оси ОХ, задана параметрическими
уравнениями
причём
и
и
непрерывны на
и
то площадь поверхности вращения
вычисляется по формуле:
.
(14)
Пример 14.
Вычислить
площадь поверхности, образованной
вращением вокруг оси ОХ одной арки
циклоиды
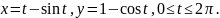
Решение.
Находим
по формуле (14) получаем
в) Площадь поверхности вращения в случае полярных координат
Если
кривая задана в полярных координатах
уравнением
,
непрерывна на
и
то
площадь поверхности вращения вычисляется
по формуле
(15)
Пример 15.
Определить площадь поверхности, образованной вращение кардиоиды вокруг полярной оси.
Решение.
Т.к. кардиоида симметрична относительно полярной оси, то искомую поверхность может быть получена и вращением дуги, описывающей верхнюю половину кардиоиды, около той же оси. Тогда пределы интегрирования по будут равны 0 и π. По формуле (15) получаем:
=
8π
.
Задание 12.
Вычислить площадь поверхности, образованной вращением дуги кривой L вокруг указанной оси.
1
L:
ось ОY.
2
L:
ось ОX.
3
L:
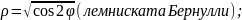ось полярная.
4
L:
ось ОY.
5
L:
ось ОX.
6
L:
ось ОX.
7
L:
ось ОY.
8
L:
ось ОX.
9
L:
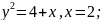ось ОX.
10
L:
ось ОX.
11
L:
ось
ОX.
12
L:
ось полярная.
13
L:
ось ОY.
14
L:
ось
ОX.
15
L:
ось ОY.
16
L:
ось ОX.
17
L:
ось ОX.
18
L:
ось ОX.
19
L:
ось полярная.
20 L: ось ОX.
21
L:
ось полярная.
22
L:
ось полярная
23
L:
ось полярная.
24
L:
ось ОX.
25
L:
ось ОY.
26
L:
ось ОX.
27
L:
ось полярная.
28
L:
ось ОX.
29
L:
ось
ОX.
30
L:
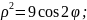ось полярная.
4. Приложения определённого интеграла к решению некоторых задач физического содержания
4.1. Вычисление пройденного пути по скорости
Пусть
- скорость движения материальной точки
по прямой. Тогда путь S,
пройденный этой точкой за время t
(t
),
вычисляется по формуле
(1)
Пример 1.
Некоторое
тело движется прямолинейно со скоростью
.
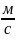Найти путь, пройденный телом за 3 секунды
после начала движения.
Решение.
По формуле (1) имеем:
