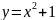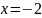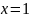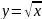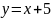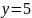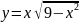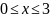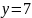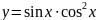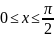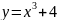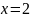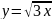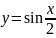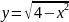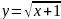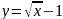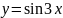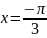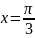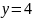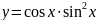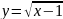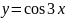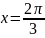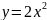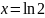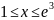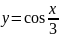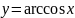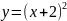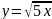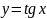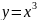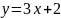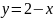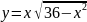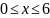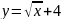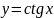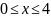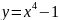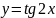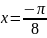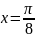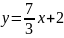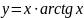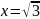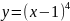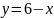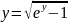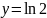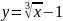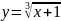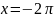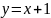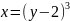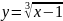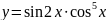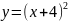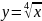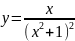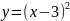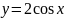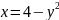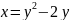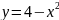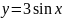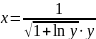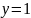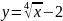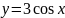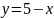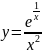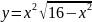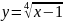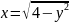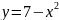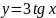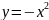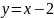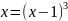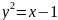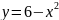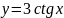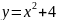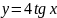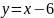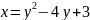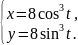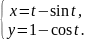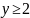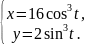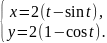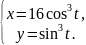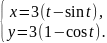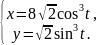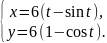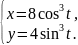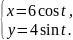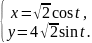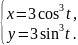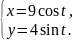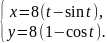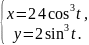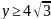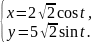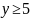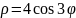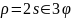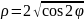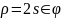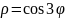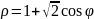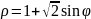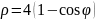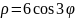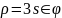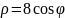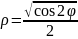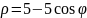- •Кафедра высшей математики Определенный интеграл и его приложения
- •Определённый интеграл
- •1. Вычисление определённого интеграла
- •2.Приближённое интегрирование
- •С пособ прямоугольников.
- •С пособ трапеций.
- •Способ парабол (Симпсона).
- •2. Площадь криволинейной трапеции, ограниченной кривой, заданной в параметрической форме
- •3. Площадь криволинейного сектора
- •3.2 Вычисление длины дуги плоской кривой
- •3.3 Вычисление объёмов тел
- •1. Объём тела с заданным поперечным сечением
- •2. Объём тела вращения
- •3.4. Вычисление площади поверхности вращения
- •4. Приложения определённого интеграла к решению некоторых задач физического содержания
- •4.1. Вычисление пройденного пути по скорости
- •4.2. Вычисление работы переменной силы
- •4.3. Вычисление силы давления жидкости на пластину
- •4.4. Вычисление координат центра масс плоской фигуры
- •5. Несобственные интегралы
- •5.1. Основные понятия
- •5.2 Признаки сравнения
2. Площадь криволинейной трапеции, ограниченной кривой, заданной в параметрической форме
Е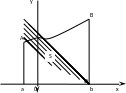 сли
кривая АВ, ограничивающая криволинейную
трапецию
сли
кривая АВ, ограничивающая криволинейную
трапецию
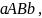 задана параметрическими уравнениями
задана параметрическими уравнениями
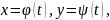
То площадь криволинейной трапеции вычисляется по формуле:
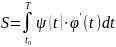 (4′)
(4′)
Кроме
того функции
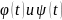 должны удовлетворять следующим условиям:
должны удовлетворять следующим условиям:
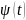 непрерывна
и неотрицательна на
непрерывна
и неотрицательна на
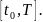
имеет непрерывную производную на
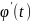 знакопостоянна
на
знакопостоянна
на
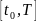 или
или
 если
если
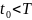 и
и
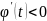 если
если
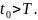
П ример
5.
ример
5.
Вычислить
площадь фигуры, ограниченной эллипсом
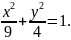
Решение.
Запишем параметрические уравнения эллипса:
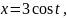
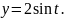
Учитывая свойства симметрии фигуры и формулу (4) получаем
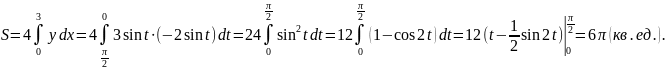
Заметим,
что пределы интегрирования
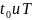 были найдены по формулам (4′):
были найдены по формулам (4′):
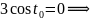

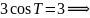
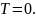
3. Площадь криволинейного сектора
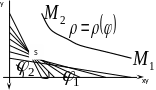
Иногда кривая может быть задана не в прямоугольной системе координат, а в полярной, уравнением
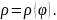
Площадь криволинейного сектора OM1M2, ограниченного дугой такой кривой и двумя полярными радиусами OM1 и OM2, соответствующими значениям 𝜑1 и 𝜑2 полярного угла, вычисляется по формуле:
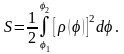 (5)
(5)
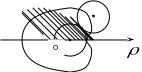
Пример 6. Найти площадь кардиоиды
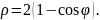
Решение.
Кардиоида
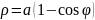 это кривая, описываемая произвольной
точкой окружности круга диаметром a,
катящейся без трения и скольжения по
неподвижной окружности того же диаметра.
Из соображений симметрии и по формуле
(5) получаем:
это кривая, описываемая произвольной
точкой окружности круга диаметром a,
катящейся без трения и скольжения по
неподвижной окружности того же диаметра.
Из соображений симметрии и по формуле
(5) получаем:
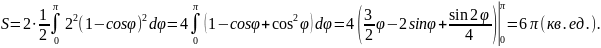
Задание 3.
Построить фигуры, ограниченные данными линиями и вычислить их площади.
№ зад № Вар. |
1 |
2 |
3 |
4 |
5 |
1 |
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
4 |
|
|
|
|
|
5 |
|
|
|
|
|
6 |
|
|
|
|
|
7 |
|
|
|
|
|
8 |
|
|
|
|
|
9 |
|
|
|
|
|
10 |
|
|
|
|
|
11 |
|
|
|
|
|
12 |
|
|
|
|
|
13 |
|
|
|
|
|
14 |
|
|
|
|
|
15 |
|
|
|
|
|
16 |
|
|
|
|
|
17 |
|
|
|
|
|
18 |
|
|
|
|
|
19 |
|
|
|
|
|
20 |
|
|
|
|
|
21 |
|
|
|
|
|
22 |
|
|
|
|
|
23 |
|
|
|
|
|
24 |
|
|
|
|
|
25 |
|
|
|
|
|
26 |
|
|
|
|
|
27 |
|
|
|
|
|
28 |
|
|
|
|
|
29 |
|
|
|
|
|
30 |
|
|
|
|
|
Задание 4.
Построить
фигуры, ограниченные линиями, заданными
параметрическими уравнениями
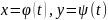 и вычислить их площади.
и вычислить их площади.
1 |
астроида |
2 |
арка циклоиды |
3 |
|
4 |
|
5 |
|
6 |
астроида |
7 |
арка циклоиды |
8 |
|
9 |
арка циклоиды |
10 |
астроида |
11 |
|
12 |
арка циклоиды |
13 |
астроида |
14 |
|
15 |
арка циклоиды |
16 |
астроида |
17 |
|
18 |
астроида |
19 |
|
20 |
арка циклоиды |
21 |
астроида |
22 |
|
23 |
арка циклоиды |
24 |
астроида |
25 |
|
26 |
арка циклоиды |
27 |
астроида |
28 |
|
29 |
|
30 |
арка циклоиды |
Задание 5.
Вычислить
площади фигур, ограниченных линиями,
заданными уравнениями в полярных
координатах
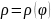 .
.
1 |
трехлепестковая роза |
2 |
трехлепестковая роза |
3 |
лемниската Бернулли |
4 |
|
5 |
|
6 |
трехлепестковая роза |
7 |
|
8 |
|
9 |
кардиоида |
10 |
трехлепестковая роза |
11 |
|
12 |
|
13 |
кардиоида |
14 |
трехлепестковая роза |
15 |
лемниската Бернулли |
16 |
|
17 |
четырёхлепестковая роза |
18 |
шестилепестковая роза |
19 |
кардиоида |
20 |
лемниската Бернулли |
21 |
|
22 |
|
23 |
четырёхлепестковая роза |
24 |
двухлепестковая роза |
25 |
|
26 |
|
27 |
кардиоида |
28 |
лемниската Бернулли |
29 |
кардиоида |
30 |
трёхлепестковая роза |