
- •Кафедра высшей математики Определенный интеграл и его приложения
- •Определённый интеграл
- •1. Вычисление определённого интеграла
- •2.Приближённое интегрирование
- •С пособ прямоугольников.
- •С пособ трапеций.
- •Способ парабол (Симпсона).
- •2. Площадь криволинейной трапеции, ограниченной кривой, заданной в параметрической форме
- •3. Площадь криволинейного сектора
- •3.2 Вычисление длины дуги плоской кривой
- •3.3 Вычисление объёмов тел
- •1. Объём тела с заданным поперечным сечением
- •2. Объём тела вращения
- •3.4. Вычисление площади поверхности вращения
- •4. Приложения определённого интеграла к решению некоторых задач физического содержания
- •4.1. Вычисление пройденного пути по скорости
- •4.2. Вычисление работы переменной силы
- •4.3. Вычисление силы давления жидкости на пластину
- •4.4. Вычисление координат центра масс плоской фигуры
- •5. Несобственные интегралы
- •5.1. Основные понятия
- •5.2 Признаки сравнения
2.Приближённое интегрирование
Вычисление определённого интеграла по формуле Ньютона – Лейбница не всегда возможно, т.к. в ряде случаев не удаётся выразить первообразную для функции f(x) через элементарные функции в конечном виде. Вычисление же определённого интеграла, исходящее из определения его (т.е. как предела интегральных сумм) часто является невыполнимым из-за технических трудностей. В таких случаях прибегают к приближённому вычислению определённых интегралов, тем более что на практике часто и не требуется знать точное значение данного интеграла.
Рассмотрим некоторые способы приближённого вычисления определённых интегралов.
С пособ прямоугольников.
Пусть
функция y=f(x)
интегрируема на
 и требуется вычислить
и требуется вычислить

Р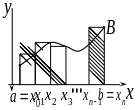 азобьём
сегмент
на n
равных
частей точками x0=a,
x1,
x2,
…, xn-1,
xn=b.
Вычислим значения функции в каждой
точке xi:
y0,
y1,
…, yn.
азобьём
сегмент
на n
равных
частей точками x0=a,
x1,
x2,
…, xn-1,
xn=b.
Вычислим значения функции в каждой
точке xi:
y0,
y1,
…, yn.
Тогда

 (1)
(1)
Эти приближённые равенства называются формулами прямоугольников. Абсолютная величина погрешности Rn здесь
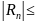
 , (2),
, (2),
где
М
– такое число, что

Если погрешность ε задана, то число делений n выбирается так, чтобы выполнялось неравенство
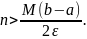
Пример 1. Вычислить по формулам прямоугольников интеграл

Решение.
Найдём сначала точное значение этого интеграла

Разделим
сегмент
 на n=11
равных частей и вычислим значения xi
и yi
на n=11
равных частей и вычислим значения xi
и yi
xi |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
yi |
1 |
4 |
9 |
16 |
25 |
36 |
49 |
64 |
81 |
100 |
121 |
144 |
По формулам (1) получаем:


Абсолютные погрешности вычислений по этим формулам
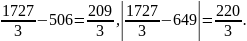
Оценим погрешность вычисления по формуле (2).
Здесь
f′(x)=2x.
Поэтому на сегменте
 ,
следовательно
,
следовательно
 .
.
Итак, способ прямоугольников самый простой и вместе с тем наиболее грубый способ приближённого интегрирования.
С пособ трапеций.
Пусть снова требуется вычислить
Разобьём на n равных частей и сохраним введённые выше обозначения.
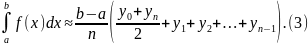
Равенство
(3) называется формулой трапеций. Для
нее абсолютная погрешность
 определяется
определяется
 (4)
(4)
где
М
– наибольшее значение f (x)
на
.
(x)
на
.
Если требуется точность ε, то число n выбирается
n< .
.
Пример 2.
Вычислим
по формуле трапеций интеграл
 который мы уже вычислим по формулам
прямоугольников.
который мы уже вычислим по формулам
прямоугольников.
Решение.
Возьмём, как и прежде, n=11, тогда по формуле (3) получаем:

Абсолютная
погрешность результата равна
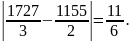
Таким образом, формула трапеций даёт результат значительно точнее, чем формулы прямоугольников.
Способ парабол (Симпсона).
Пусть
требуется вычислить

Разбив на 2n равных частей и сохранив введённые выше обозначения, имеем

Это так называемая формула парабол (формула Симпсона).
Абсолютная погрешность R2n:

где
М
– наибольшее значение

Пример 3.
Вычислить приближённо

Решение.
Найдём сначала точное значение этого интеграла по формуле Ньютона – Лейбница
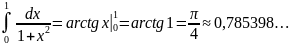
Вычислим теперь приближённое значение его по формулам (1) и (3). Пусть n=10.
-

0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1

1,00000
0,99010
0,96154
0,91743
0,86207
0,80000
0,73529
0,67114
0,60976
0,55249
0,50000
По
второй формуле прямоугольников получим
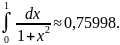 Верен только один десятичный знак.
Верен только один десятичный знак.
По
формуле трапеций (3) получим
 верны уже два десятичных знака.
верны уже два десятичных знака.
Теперь
вычислим этот интеграл по формуле
Симпсона, для чего разделим сегмент
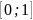 всего на 4 части, тогда
всего на 4 части, тогда
|
0 |
|
|
|
|
|
1,0 |
0,94118 |
0,8 |
0,64 |
0,5 |
Согласно формуле (5) получаем:
 где
все пять десятичных знаков верны.
где
все пять десятичных знаков верны.
Задание 2.
Вычислить точное значение определённого интеграла I по формуле Ньютона – Лейбница. Вычислить этот же интеграл приближёнными способами: в способах прямоугольников и трапеций задать n=10, в способе парабол n=4. Найти относительные погрешности приближённых вычислений δ1, δ2 и δ3.
Примечание.
δ= где
где
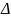 -
абсолютная погрешность,
-
абсолютная погрешность,
x - точное значение.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. Приложение определённого интеграла
к задачам геометрии
3.1 Вычисление площадей плоских фигур
1. Площадь в прямоугольных координатах
При
постановке задачи определённого
интегрирования было показано, что
определённый интеграл в случае, когда
 ,
с геометрической точки зрения определяет
площадь криволинейной трапеции
,
с геометрической точки зрения определяет
площадь криволинейной трапеции
 ,
т.е. фигуры , ограниченной п
,
т.е. фигуры , ограниченной п рямыми
рямыми
 и кривой
и кривой
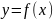 ,
где
,
где
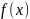 - неотрицательная, непрерывная на
функция.
- неотрицательная, непрерывная на
функция.
 (1)
(1)
Площадь всякой плоской фигуры можно рассматривать как сумму или разность площадей некоторых криволинейных трапеций. Это означает, что с помощью определённых интегралов можно вычислить площади любых плоских фигур.
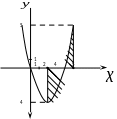
Пример 1.
Вычислить
площадь фигуры, ограниченной линиями

Решение.
Вначале построим фигуру, ограниченную данными линиями, предварительно приведя уравнение параболы к каноническому виду.
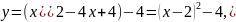

Это
парабола с вершиной в точке О′(2;-4), ветви
направлены вверх, параметр
 .
.
Искомая
площадь
 поэтому
поэтому
 +
+
Ф игуру,
ограниченную прямыми
игуру,
ограниченную прямыми
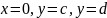 и кривой
и кривой
 ,
где
,
где
 также называют криволинейной трапецией
также называют криволинейной трапецией
 .
Площадь её вычисляется по формуле
.
Площадь её вычисляется по формуле
 (2)
(2)
Пример 2.
В ычислить
площадь фигуры, ограниченной осью Оу
и параболой
ычислить
площадь фигуры, ограниченной осью Оу
и параболой

Решение.
Найдём сначала ординаты точек пересечения параболы с осью Оу:

Находим площадь по формуле (2)
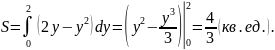
П лощадь
фигуры, ограниченной двумя кривыми
лощадь
фигуры, ограниченной двумя кривыми
 и
и
 и двумя вертикальными прямыми
и двумя вертикальными прямыми
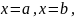 причём
причём
 при
при
 очевидно, легко вычислить как разность
площадей криволинейных трапеций
очевидно, легко вычислить как разность
площадей криволинейных трапеций
 и
и
 т.е.
т.е.
 (3)
(3)
Пример 3.
Вычислить
площадь фигуры, ограниченной линиями

Решение.
П риведём
уравнения парабол к каноническому виду:
риведём
уравнения парабол к каноническому виду:
 – парабола,
вершина в т. О (0;0), ветви направлены
влево, параметр
– парабола,
вершина в т. О (0;0), ветви направлены
влево, параметр

 – парабола,
вершина в т. О′ (1;0), ветви направлены
влево, параметр
– парабола,
вершина в т. О′ (1;0), ветви направлены
влево, параметр
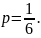
Найдём точки пересечения, приравняв уравнения парабол:


Из рисунка видно, что для вычисления площади данной фигуры удобнее интегрировать по оси Оу:
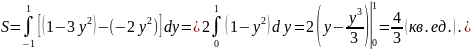
К огда
плоская фигура ограничена дугами
нескольких кривых, её разбивают на части
прямыми, параллельными оси Ох ( или оси
Оу) так, чтобы к вычислению площади
каждой полученной части можно было
применить используемые ранее формулы.
Площадь всей фигуры вычисляется как
алгебраическая сумма площадей частей,
на которые оказалась разбитой данная
фигура.
огда
плоская фигура ограничена дугами
нескольких кривых, её разбивают на части
прямыми, параллельными оси Ох ( или оси
Оу) так, чтобы к вычислению площади
каждой полученной части можно было
применить используемые ранее формулы.
Площадь всей фигуры вычисляется как
алгебраическая сумма площадей частей,
на которые оказалась разбитой данная
фигура.
П ример
4.
ример
4.
Вычислить
площадь фигуры, ограниченной линиями
 ,
,

Решение.
Решая системы:

Находим
абсциссы точек пересечения прямой
 с параболами
и
с параболами
и
 Прямой
Прямой
 разобьём данную фигуру на две части –
ОАСО
и САВС.
Площадь S
данной фигуры равна сумме площадей этих
частей:
разобьём данную фигуру на две части –
ОАСО
и САВС.
Площадь S
данной фигуры равна сумме площадей этих
частей:





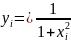


 .
.
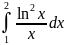 .
.






 .
.
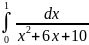 .
.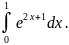
 .
.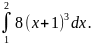
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.