Современные алгоритмы и теория связи

До сих пор теоретическая информатика изучала вычислительные модели, соответствующие концепции фон Неймановских машин. Но сейчас на первый план выходит работа с компьютерными сетями. Настоящее текущее понятие “вычисление” требует нового подхода и новых научных разработок. В этом состоит одна из главных задач современных исследований в информатике.

В первую очередь это вопросы, относящиеся к распределенным вычислениям. Пользователь, связь пользователя с многими другими компьютерами и сам процесс вычислений должны рассматриваться как единый процесс. И все это завязано на новые технологии разработки ПО. В то же время само ПО жестко связано и напрямую зависит от используемого АО, а оно столь же стремительно развивается как и ПО.

Внедрение каждой новой технологии это целый букет проблем , связанных с разработкой и оптимизацией алгоритмов.

Современные алгоритмические идеи решения самых разнообразных задач часто опираются на результаты теории простых чисел. Известная криптосистема RSA (Риверст, Шамир, Адлеман) использует ряд алгоритмов из теории простых чисел в том числе некоторое обобщение малой теоремы Ферма и алгоритм Евклида.

Теорема Ферма- Эйлера (малая теорема Ферма) о делимости в элементарной теории чисел.

Введем операцию умножения чисел по модулю n, a * b mod n и определим степени числа:

a² = (a * a) mod n ,

a^k+1 = (a^k * a) mod n.

Для любого простого числа p и числа a, 0 < a < p, справедлива малая

теорема Ферма:

a ^p-1 1 (mod p)

или a ^p-1 -1 делится на р.

Доказательство выполняется методом индукции.

Замечание: Говорят, что два числа а и b сравнимы по модулю с, если они дают при делении на с равные остатки. Операция получения остатка от деления а на с записывается в виде: a mod c = d, что эквивалентно представлению : a =k*c+d, d>=0, k>=0 - целые числа. Сравнимость двух чисел по модулю с означает, что a mod c = b mod c и записывается в виде a b (mod c). Если a 0 (mod c), то число а делится на число с без остатка.

Тест Миллера – Рабина

Вероятностный и эффективный тест Миллера – Рабина применяется в криптографических алгоритмах, и там возникает необходимость нахождения больших простых чисел.

Идея теста состоит в последовательной генерации случайных чисел и проверке их на простоту с использованием теоремы Ферма – Эйлера. Основная задача теста связана с уменьшением вероятности ошибочного признания некоторого составного числа в качестве простого.

Вероятность ошибки теста экспоненциально падает с ростом успешных проверок с различными значениями целых чисел , а именно, если выполнено s успешных проверок, то вероятность ошибки составляет 2^-s . Это реально приводит к выбору s в пределах нескольких десятков.

Алгоритм Рабина- Карпа

Это алгоритм поиска подстроки в строке. Главная идея связана с переходом к сравнению чисел вместо сравнения образца и части строки поиска.

Этот метод успешно применяется в вычислительной молекулярной биологии для поиска совпадающих цепочек ДНК и расшифровки генов.

Генетические алгоритмы

– это алгоритмы, которые используют биологические механизмы поиска наилучших решений. Их называют “природные вычисления”.

Это научное направление объединяет кроме генетических алгоритмов еще и эволюционное программирование, нейросетевые вычисления, клеточные автоматы и ДНК- вычисления, муравьиные алгоритмы.

Исследователи обращаются к природным механизмам, которые миллионы лет обеспечивают адаптацию биоценозов к окружающей среде, используя, например, механизм наследственности.

Генетические алгоритмы при решении задачи оптимизации стремятся найти лучшее возможное, но не гарантировано оптимальное решение.

Генетические алгоритмы успешно применяются для решения задач оптимизации в пространстве состояний с большим количеством измерений, в экономических задачах оптимального характера, например, задачи распределения инвестиций.

Смотри : Рутковский Л, Нейронные сети, генетические алгоритмы и нечеткие системы, 2004г

Муравьиные алгоритмы часто используют в задачах оптимизации в графах.

Смотри : Штовба С.Д. Муравьиные алгоритмы, 2003г

Открытое поле деятельности представляет работа с компьютерными сетями . Это сложный взаимосвязанный мир, полный непредсказуемых и асинхронных действий. Здесь много нерешенных вопросов, проблем, связанных с распределенными вычислениями, надежностью. Это связано и с технологиями разработок по ПО, и с используемым аппаратным обеспечением, особенно оптическими сетями. Приход каждой новой технологии открывает целый ряд новых проблем в области разработки и оптимизации алгоритмов.

Криптология – в переводе означает секретное письмо. Состоит из двух частей :

• криптография – разработка криптосистем ;

• криптоанализ – математические методы нарушения конфиденциальности информации без знания ключа.

Классическая криптографическая система

Формально система записывается как тройка (K, A, S) , где

• K – множество всех допустимых вариантов текста

• A – множество всех возможных криптотекстов

• S - множество ключей

Криптография необходима для обмена информацией через открытые коммуникационные каналы. У классических систем как механизм шифрования ,так и механизм дешифровки определяется с помощью ключа, являющегося общим секретом отправителя и получателя. У криптосистем с открытым ключом такого секрета нет. Знание ключа кодирования не поможет найти ключ дешифровки (концепция односторонних функций). Обратную функцию вычислить нельзя без дополнительных знаний, известных только получателю.

Лекция 13

Формальные теории , формальные системы и формальные языки

Теории бывают содержательными и формальными. Химия, физика биология –содержательные. К ним в какой – то мере можно отнести и информатику. Все они используют практику, создают модели реальных объектов.

И сама математика может быть содержательной, если она применяется на практике. Исследования основ математики, начатые исключительно в целях обоснования самой математики как метода в науке, привело к созданию математической логики, теории формальных систем и теории алгоритмов, ставших основой создания компьютерной науки (теоретической информатики). Содержательность формальной теории заключена в ее интерпретациях.

Прежде чем ввести формальный язык информатики нам придется кратко повторить элементы теории множеств.

Одно время казалось, что теория множеств позволит построить математику как логически безупречную науку, имеющую критерий истинности внутри себя. Французский математик Пуанкаре писал, что с введением теории множеств в математике достигнута абсолютная строгость. Но развитие математики и в том числе теории множеств опровергло эти амбициозные претензии Пуанкаре. В начале 20 века в теории множеств были обнаружены противоречия ( парадоксы), не разрешенные целиком и сегодня (Это связано с обыкновенными и необыкновенными множествами (одни не содержат самих себя в качестве элементов, таких большинство, другие содержат). Но есть такие множества, которые невозможно отнести ни к тем, ни к другим. Например, множество всех людей на земле - это не человек. Множество всех натуральных чисел – это не натуральное число. Но множество всех мыслимых множеств – само является множеством. Но попробуйте ответить на вопрос каким является множество всех обыкновенных множеств – обыкновенным или необыкновенным ? Вы увидите, что попытка найти ответ приводит нас к противоречию. Попытайтесь сделать это самостоятельно.

И вот тут-то выявилось, что теория множеств, лежащая в основе современной математики, внутренне противоречива. Это не может подорвать доверия к прикладным результатам, но опровергает абсолютную строгость математики. А тут еще Тарский своими работами по математической логике показал, что грамматика естественных языков не обладает однозначностью для того, чтобы обеспечить абсолютную строгость доказательства (пример с переводом на несколько языков). Для преодоления неоднозначности естественных языков были разработаны целиком формализованные языки математической логики. Но они слишком сложны, поэтому математические работы пишутся на естественных языках.

Потом ввели аксиоматический метод. Это способ построения научной теории, при котором за основу берется ряд основополагающих, не требующих доказательства положений этой теории, называемых аксиомами. Для того чтобы сделать возможным точное рассмотрение доказательства, им придали единую точно определенную форму с помощью формализации теории (Гильберт) : математическая теория заменяется формальной системой. В результате стало возможным представлять не формализованные до конца математические теории как точные математические объекты.

Формальная теория строится как четко определенный класс выражений, формул, в котором некоторым точным способом выделяется подкласс теорем данной формальной системы. При этом формулы формальной системы непосредственно не несут в себе никакого содержательного смысла, они строятся из произвольных символов, исходя лишь из соображений удобства.

Общая схема построения формальной системы:

• Язык системы :

алфавит,

синтаксис.

• Аксиомы системы – конечное или перечислимое множество формул.

• Правила вывода системы.

Введем формальный язык информатики и способы представления объектов, задач, целей.

Компьютер работает с текстами, выполняя вычислительный процесс. Тексты являются последовательностями символов некоторого алфавита.

Любой вычислительный процесс можно рассматривать как преобразование одного текста в другой, так как входные и выходные данные есть тексты. Программа тоже является текстом над алфавитом, состоящим из символов клавиатуры компьютера.

Все данные, представленные в компьютере как последовательности 0 и 1 , любые входы и выходы тоже являются текстами, по крайней мере могут интерпретироваться как тексты над подходящим алфавитом. С этой точки зрения каждая программа преобразовывает входные тексты в тексты выходные. Поэтому важно ознакомиться с принципами работы с текстами, которые используются для разработки формальных описаний алгоритмических проблем.

Подходящий формализм для работы с текстами – это понятия алфавита, слова и языка.

Прежде чем перейти к алфавитам, словам и языку, напомним некоторые определения, обозначения и основные свойства множеств.

МНОЖЕСТВА.

Множества состоят из элементов.

Если мы пишем x S , это означает, что объект x является элементом множества S.

Если мы пишем x S , это означает, что объект x не является элементом множества S.

Можно задать множество перечислением его элементов через запятые в фигурных скобках. Например, S={1,2,3,4,5} содержит элементы 1,2,3,4,5 и только их. Число 5 является элементом данного множества, а число 6 нет, то есть

5 S , а 6 S

• Множество не может содержать двух одинаковых элементов.

• Порядок элементов не фиксирован.

• Два множества А и В равны, если они состоят из одних и тех же элементов.

В этом случае пишут А=В.

Например, {1,2,3}={3,1,2}

Имеются специальные обозначения:

• обозначает пустое множество, не содержащее ни одного элемента.

• Z – обозначает множество целых чисел (Z={….-2,-1,0,1,2,….}

• R - обозначает множество вещественных (действительных) чисел

• N - обозначает множество натуральных чисел (N=1,2,…..) или N={0,1,2,…}

Если все элементы множества А являются элементами множества В (из x A следует x B), говорят, что А является подмножеством множества В и пишут А В. Если при этом А не совпадает с В , то А называется собственным подмножеством множества В; в этом случае пишут А В. Для любого множества А выполнимо соотношение А А. Множества А и В равны тогда и только тогда, когда А В и В А. Для любых трех множеств А, В, С из А В и В С следует А С. Для любого множества А имеет место соотношение А.

Мы можем выделить из множества А все элементы, обладающие некоторым общим свойством, и образовать из них новое множество В.

Например, множество четных чисел можно определить так: {x : x Z и x/2 –целое число}. Иногда вместо двоеточия используется вертикальная черта.

Лекция 14

Теоретико – множественные операции для любых множеств А и В.

• Пересечение (intersection) множеств А и В определяется как множество

элементов, принадлежащих одновременно и А , и В.

A B = { x : x A и x B };

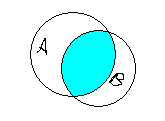
• Объединение (union) множеств А и В определяется как множество, состоящее из элементов, принадлежащих хотя бы одному из них.

A B = { x : x A или x B };

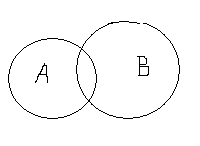
• Разность (difference) множеств А и В определяется как множество элементов, принадлежащих одному их них и не принадлежащих другому.

A \ B = { x : x A и x B };

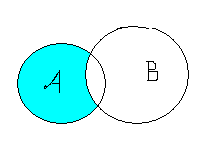
A \ B

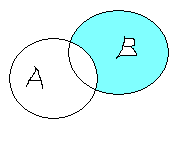
B \ A

• Декартово произведение двух множеств А и В определяется как множество всех упорядоченных пар, у которых первый элемент принадлежит А, а второй - В. Обозначается А В.

А В = {(a,b): a A и b B}

Пример

{a,b} {a,b,c}= { (a,a), (a,b), (a,c), (b,a), (b,b), (b,c)}

Для конечных множеств А и В мощность их произведения равна произведению мощностей:

|A B| =|A| * |B| .

Декартово произведение n множеств А_1, А₂, …., А_n определяется как множество n-ок :

A₁ A₂ ….. A_n = {(a_1, a₂, ….. ,a_n) : a_i A_i при всех i=1,2,….,n}

Число элементов в декартовом произведении равно произведению мощностей сомножителей:

| A₁ A₂ …. A_n | = | A₁ | *| A₂ |*….| A_n |.

Декартова степень

Aⁿ = A A …. A.

Для конечного А мощность Аⁿ =| A | ⁿ .

Свойства теоретико-множественных операций

• Свойства пустого множества

A = , A =A;

• Идемпотентность –

это действие, многократное повторение которого не приводит к изменениям иным, нежели при однократном. В компьютерах, например, сервер должен возвращать одни и те же ответы на идентичные запросы. Это позволит кешировать ответы, снижая нагрузку на сеть.

A A = A, A A = A;

В частности A =A, A = ,

A U = U, A U = A.

• Коммутативность -

A B =B A, A B = B A;

• Ассоциативность Например, в программировании ассоциативность (очередность) операторов – это последовательность их выполнения, реализуемая, когда операторы имеют одинаковый приоритет и отсутствуют явно обозначенные скобки, которые этот приоритет могут нарушить.

A (B C) = (A B) C, A (B C) = (A B ) C;

• Дистрибутивность

A (B C) = (A B) (A C),

A (B C) = (A B) (A C);

• Законы поглощения

A (A B) = A, A (A B ) = A;

• Законы де Моргана (двойственности)

A \ (B C ) =(A \ B) (A \ C),

A \ (B C ) =(A \ B) (A \ C).

Можно множество рассматривать как подмножество некоторого фиксированного множества, называемого универсумом. Если, например, речь идет о множестве целых чисел, то в качестве универсума можно взять множество Z целых чисел. Если универсум U фиксирован, можно определить

_ _

дополнение множества А как А=U \ A. Для любого А U верны такие утверждения:

= _ _

A= A, A A= , A A =U.

Из законов де Моргана следует, что для любых множеств А, В U имеет место равенство:

______ _ _ ______ _ _

A B = A B, A B = A B.

Два множества А и В называются непересекающимися, если они не имеют общих элементов, то есть если

А В= .

Говорят, что семейство S={S_i} непустых множеств образует разбиение множества S на классы, если:

• Множества S_i попарно не пересекаются, то есть

S_i S_j = при i j,

• Их объединение есть S, то есть

S= S_i .

s_i s

Это значит, что семейство S образует разбиение множества S , если любой элемент множества s S принадлежит ровно одному из множеств S_i семейства.

Два множества имеют одну и ту же мощность, если между их элементами можно установить взаимно однозначное соответствие.

Мощность пустого множества равна нулю | |=0.

Мощность конечного множества - натуральное число.

Множества, элементы которых можно поставить во взаимно однозначное соответствие с натуральными числами, называются счетными.

Множество целых чисел Z–счетно.

Множество вещественных чисел R – несчетно.

Элементы КОМБИНАТОРИКИ в приложении к множествам

Комбинаторика – это математика счета. В вычислительной технике и программировании часто встречаются несколько типов счетных задач. Обычно их решение связано с логикой и проницательностью.

Число комбинаторных задач быстро растет. К их решению приводят многие практические задачи. Но они только выглядят простыми. В большинстве своем они достаточно трудны. Для многих из них до сих пор не найдены решения.

Какие задачи решаются комбинаторными методами?

• Задачи на размещения. Это задачи о расположении, например, на плоскости предметов, обладающих свойствами дальнодействия.

• Задачи о покрытиях и заполнениях – например, задачи о заполнении заданных пространственных фигур меньшими телами заданных форм и размеров.

• Задачи о маршрутах. Задачи нахождения кратчайшего пути, задачи оптимального планирования и т.п.

• Комбинаторные задачи теории графов.- задачи сетевого планирования, задачи окрашивания графов, задачи транспортных и электрических сетей и т.д.

• Перечислительные задачи – нахождение числа предметов, составленных из данного набора элементов при соблюдении определенных условий.

В задачах комбинаторного анализа исследуются чаще всего дискретные множества.. особенность таких задач заключается в том, что в них главное внимание уделяется двум видам операций – отбору подмножеств и упорядочению элементов. Эти две операции являются основными в комбинаторике.

Отбор подмножества связан с понятием выборки.

Подмножество из r элементов, выбранное из множества S_n , состоящего из n элементов, называется ( n, r ) – выборкой, а r - объемом этой выборки.

Если (n, r ) - выборки рассматриваются с учетом порядка элементов в них, то они называются (n, r ) – перестановками. ( permutation)

Если порядок элементов в выбранных подмножествах не важен, то соответствующие выборки называются ( n, r ) – сочетаниями. (combination).

Пример

Пусть дано множество A={a, b, c} , объем выборки r=2.

Указать все упорядоченные и неупорядоченные выборки с повторениями и без повторений из трех элементов по два.

Решение

1. aa, ab, ac, ba, bb, bc, ca, cb, cc ----- 9 перестановок с повторениями ( P_3,2=9)

2. ab, ac, ba, bc, ca, cb -6 престановок без повторений (P_3,2= 6)

3. ab,ac,bc – 3 сочетания без повторений (C₃²=3)

4. aa, ab, ac, bb, bc, cc - шесть сочетаний с повторениями(C₃²=6).

Существуют три основных правила счета, из которых получаются все остальные.

(правила сложения, правило умножения и перестановки) Важно понять, какое конкретное правило надо применять в вашей задаче.

• Правило суммы ( сложения)

Если существует |А| вариантов из множества А и |В| вариантов из множества В, то тогда существует |А|+|В| вариантов, что случится А или В при условии, что элементы А и В различны.

| A B |= | A |+ | B |.

Пример

Например, если у вас есть 5 рубашек и 4 брюк и в прачечной повредили одну из вещей, то тогда существует 9 возможно поврежденных вещей.

Пример

Если символ на номере машины должен быть либо русской буквой, либо цифрой, то всего есть 33+10=43 возможности , так как букв 33, а цифр 10.

• Правило умножения

Если существует |A| вариантов из множества А и |B| вариантов из множества В, то тогда существует |А| |В| комбинаций одного варианта из множества А и одного варианта из множества В.

| A | | B | = | A |* | B |.

Пример

Вы изучаете в семестре 10 предметов. В пятницу у вас 4 разных предмета. Сколькими способами можно составить расписание на пятницу?

Это 4 перестановки без повторения из 10 элементов. Первое занятие можно записать в расписание 10 способами. Второе занятие – девятью, третье- восемью, четвертое –семью. По правилу произведения число способов составления расписания A₁₀⁴=10*9*8*7=5040

Пример

Например, пусть у вас есть 5 рубашек и 4 брюк. Тогда у вас есть 5*4=20 различных вариантов костюмов на завтра.

Пример

Пусть есть 10 блинчиков и 5 видов начинки к ним. 10*5 =50 вариантов блинчиков с начинкой можно получить.

• Строки

Строкой (string) назовем конечную последовательность элементов некоторого конечного множества S (алфавита) . Например, существует 8 двоичных ( составленных из 0 и 1 ) строк длиной 3:

000, 001, 010, 011, 100, 101 , 110, 111.

Подстрокой строки s называется последовательность идущих подряд элементов строки s. Говоря о k-подстроке имеют в виду подстроку длиной k. Так , 010 является 3- подстрокой строки 01101001. она начинается с позиции 4, а 111 –нет. Строка длины k из элементов множества S является элементом прямого произведения S^k , так что всего существует |S|^k строк длины k. В частности, имеется 2^k двоичных строк длины k.

• Формула включений – исключений. Правила сложения являются специальным случаем более общей формулы, когда два множества могут пересекаться:

|A B|= |A| + |B| – |A B|.

Например, А- набор расцветок моих рубашек, а В – расцветки моих брюк. Используя эту формулу, я могу посчитать общее число расцветок, если я знаю, какая одежда совпадает по цвету и наоборот. Причина, по которой это срабатывает, состоит в том, что при сложении множеств мы два раза считаем определенные варианты, которые входят и в то и в другое множество.

Проблема двойного счета – неприятный аспект комбинаторики, который может затруднить решение задачи с помощью включений-исключений.

Есть еще методика под названием биекция. Это взаимно - однозначное соответствие между элементами одного множества и другого. Если такое соответствие есть, то при подсчете размера одного множества вы автоматически получаете размер другого. Для использования биекций нужен набор множеств, которые мы умеем считать, тогда можно привязать к ним другие объекты. Наиболее часто мы применяем следующие комбинаторные объекты:

• Перестановки. Набор n упорядоченных объектов, в котором каждый объект встречается ровно один раз, называется перестановкой. Всего существует

n != различных перестановок.

Например, 3!=6 перестановок трех объектов: 123, 132, 213, 231, 312, 321.

Для n=10 имеем n! =3628800, так начинаем приближаться к пределу возможностей полного перебора. Поэтому хорошо бы знать, с какой скоростью растет число объектов, чтобы определиться, когда полный перебор перестанет подходить нам в качестве алгоритма.

• Подмножества. Произвольная выборка элементов из n возможных объектов, называется подмножеством. Для n объектов существует 2ⁿ различных подмножеств. Таким образом, 2³ =8 подмножеств трех объектов:1,2,3, 12,13,23.123 и пустое множество. Для n= 20 имеем 2ⁿ =1048576, так что начинаем приближаться к пределу возможностей полного перебора.

• Размещения без повторений

Когда каждый элемент можно использовать только один раз, но не требуется использовать все элементы, то говорят о размещениях без повторений.

Пусть фиксировано множество S из n элементов и некоторое k, не превосходящее n. Размещением без повторений из n по k называют последовательность длины k, составленную из различных элементов S. Число таких размещений равно

n*(n-1)*(n-2)*…….*(n-k+1)=n! / (n-k)!

Так как существует n способов выбора первого элемента, n-1 способов выбора второго элемента , и так далее до k-ого элемента, который можно выбрать n-k+1 способами.

Например, существует 12=4*3 последовательностей из двух различных элементов множества {a,b,c,d}:

a b , a c , a d , b a , b c , b d , c a , c b , c d , d a , d b , dc.

Частным случаем этой формулы является формула для числа перестановок( так как перестановки являются частным случаем размещений при n=k.

• Размещения с повторениями.(Strings). Это последовательность символов, набираемая с возможностью повторения.

Существует mⁿ различных последовательностей из n объектов m различных видов.

27 размещений длиной 3 для набора 123: 111, 112, 113, 121, 122, 123, 131, 132, 133, 211, 212, 213, 221, 222, 223, 231, 232, 233, 311, 312, 313, 321, 322, 323, 331,332, 333. Число двоичных размещений длины n равняется числу подмножеств n объектов, и число возможных вариантов растет еще быстрее с увеличением m.

• Сочетания из n элементов по k называются k-элементные подмножества какого-либо n-элементного множества. Например, у множества {a,b,c,d} из 4 элементов имеется 6 двухэлементных подмножеств

{a,b} , {a,c} , {a,d} , {b,c} , {b,d} , {c,d}.

Число сочетаний из n по k в k! раз меньше числа размещений без повторений( для тех же n и k),так как из каждого сочетания из n элементов по k можно сделать k! размещений без повторений, переставляя его элементы. Поэтому число сочетаний из n элементов по k равно

n!/ k!(n-k)!

Для k=0 эта формула дает 1, как и должно быть , т.к. есть ровно одно пустое подмножество. Напомним, что 0!=1.

• Биномиальные коэффициенты

Для числа сочетаний из n по k используется обозначение C_n^k или :

C_n^k =n! / k!(n-k)!

Эта формула симметрична относительно замены k на n-k:

C_n^k =C_n^n-k .

Числа C_n^k называют биномиальными коэффициентами, появляющимися в биноме Ньютона:

(x+y)ⁿ =

( если раскрыть скобки в (x+y)ⁿ , то количество членов, содержащих k множителей x и n-k множителей y равно количеству способов выбрать k мест из n , то есть C_n^k ).

При x=y=1 ,бином Ньютона дает

2^т =

(Комбинаторный смысл: 2ⁿ двоичных строк длины n сгруппированы по числу единиц: имеется как раз C^k_n строк с k единицами.)

Оценки биномиальных коэффициентов

Для 1<=k<=n имеем оценку снизу

C_n^k >=

Оценка сверху:

C_n^k <=

Посмотреть шенноновскую энтропию и 2.12

Рекуррентные соотношения

Очень полезны при работе с рекурсивно заданными структурами, такими как списки, деревья, Рекуррентно можно представить любой полином.

Рекуррентное равенство, определенное через себя самого.

Примеры:

a_n=a_n-1 + 1, a₁=1 -> a_n=n.

a_n=2a_n-1, a₁=2 -> a_n=2ⁿ.

a_n=na_n-1, a₁=1 -> a_n=n!

Замечание: Компьютерные программы легко вычисляют значение заданного рекуррентного соотношения, даже если аналитической формы не существует.

Рекурсия и индукция рассмотрены в лекции№1.

Самостоятельный тренинг:

1. Даны два отрезка А=[1,3] и В=[2,4].

Найти: их объединение, пересечение, разность .

2. Дано: A={-6,-3,0,3,6}, B={0,2,4,6,8} .

Найти : объединение множеств

3.Зная, что С_n^k =C_n-1^k +C_n-1^k-1 составьте таблицу для C_n^k при n=0,1,2,…6 и при k от 0 до n в виде равнобедренного треугольника ( C⁰₀ сверху, C₁⁰ и C₁¹ в следующей строке и так далее) Этот треугольник называют треугольником Паскаля.

4 Сколько имеется пятизначных чисел, которые делятся на пять?

5. Сколько есть двузначных чисел, у которых обе цифры четные?

6. Сколькими способами можно посадить за круглый стол n мужчин и n женщин так, чтобы никакие два лица одного пола не сидели рядом?

Лекция 15

Алфавиты, слова, языки.

Для обработки информации мы представляем данные (объекты обработки) как последовательности символов. Мы фиксируем для представления данных специальный набор символов – алфавит.

Определение: Алфавитом называется любое непустое конечное множество. Каждый элемент алфавита называется символом.

Для представления нужных нам объектов мы можем выбрать любой алфавит, содержащий конечное число символов.

Примеры:

_bool ={0,1} –булевский алфавит

_лат ={a,b,c,d,…..,z} –латинский алфавит

_keyboard = _лат {A,B,C,… , >,<,(,), …..,!} – алфавит всех символов на клавиатуре

_ип1п = _лат {A,B,C,…Z} { , ,&, } { } N₀ –алфавит для языка исчисления предикатов 1 порядка

Здесь N={1,2,3,…….} –множество натуральных чисел

N₀=N {0}

_m ={0,1,2,….,m-1} для каждого m >=1 – алфавит для записи чисел в m-ичной системе счисления.

Определим слово как некоторую последовательность символов. Слово у нас будет означать произвольный текст.

Определение Пусть - некоторый алфавит. Слово над - любая конечная последовательность символов алфавита .

Пустое слово - единственное слово, состоящее из нулевого количества символов.

Длина слова w над , обозначаемая как | w | , есть число символов в этом слове.

^* - множество всех слов над алфавитом .

⁺= ^*- { } - означает множество всех слов за исключением пустого.

Символ пробела над алфавитом клавиатуры отличен от , так как пробел –элемент алфавита _keyboard , то | пробел|=1.

Примеры

1. ( _bool)^*={ ,0,1,00,01,10,11,000,001,010,100,011,…..}

= { } {x₁ x₂ ……x_i | i N₀, x_{j bool} для j=1,…,i}

Мы видим, что существует возможность перечисления всех слов над заданным алфавитом. При этом слова записываются в порядке возрастания их длин, то есть одно слово за другим для каждой рассматриваемой длины.

2.Дан двухбуквенный алфавит ²={a,b}

( ^{+ 2}) - это множество слов, состоящих из двух букв, прописанных в произвольном порядке за исключением пустого.

Например, множество всех слов длины 2 :

+ ²={aa, bb, ab, ba};

Упражнения:

1.Напишите множество всех слов длины 3;

( + ³={aaa, aab, bba, bbb, aba, abb, baa, bab}) – ответ и так далее для любого n.

Отсюда также видно, как подсчитать сколько слов определенной длины существует над заданным алфавитом .(у нас =8))

2 Пусть дан язык ₁={aⁿb^m} ; n=1,2….., m=1,2….

Определить, принадлежит ли слово aabbb данному языку.

( да, принадлежит)

А слово bab?

(нет, не принадлежит)

3 Пусть дан язык ₂={aⁿbⁿ}; n=1,2…..

Определить, принадлежит ли слово aaaabbbb данному языку?

(да)

? abab?

(нет)

? bbaa?

(нет)

Принадлежат те, которые имеют одинаковое число букв a и b и начинаются с a.

Слова можно использовать для представления различных объектов – это могут быть, например, числа, формулы, графы, деревья, программы.

Слово x = x₁ x₂ …..x_n ( _bool)^* , x_{i bool} для i=1,….,n

можно рассматривать как двоичное представление неотрицательного числа

Number(x) = (2⁰*1+2¹*0+2²*1+….)

Наоборот, для любого неотрицательного целого числа m запись

Bin(m) ( _bool)^*

обозначает наиболее короткое двоичное представление числа m.( Наиболее короткое означает, что первый символ должен быть равен единице). Поэтому

Number(Bin(m))=m.

Как определить зеркальный язык?

₄= {aa^-1} , где a ⁺

Слова abba ₄, baaaab ₄ , а слова aba и aaa не принадлежат ₄.

Вывод:

Мы видим, что любой язык суть некоторое n-арное отношение на множестве всех слов ⁺, где n=1,2……(арность – это размерность)

Давайте представим булевскую формулу с помощью операторов отрицания, конъюнкции и дизъюнкции ( ). Для этого будем использовать алфавит

_лог = {0,1,x,(,), }

где x –булевы переменные, используемые как символы алфавита (x_1, x₂,…..) и кодировка булевской переменной x_i как слова

xBin(i) для всех i N.

Все остальные символы в формуле переписываются в ее представлении один к одному. Тогда формула

(x₁ x₇) (x₁₂) (x₄ x₈ (x₂))

имеет следующее представление:

(x1 x111) (x1100) (x100 x1000 (x10)).

Полезная операция над словами – простая конкатенация двух слов.

Определение Пусть - некоторый алфавит. Конкатенация относительно - это отображение K : ^{* * *}, заданное в виде

K(x,y)=x*y=xy

для всех x, y ^*

Пример

Пусть x=0aa1bb и y=111b для ={0,1,a,b}.

Тогда K(x,y) = x*y=0aa1bb111b.

Замечания

1. Конкатенация K для -ассоциативная операция над ^* , так как

K(u, K(v,w)) = u*(v*w) = uvw = (u*v)*w =( K (K(u, v), w)

для всех u,v,w ^*

2.Кроме того, для каждого x ^* выполнено следующее:

x * = * x =x

3. Конкатенация коммутативна только для алфавитов, состоящих из одной буквы.

4. Для всех x,y ^* ,

| xy | =|x*y| = |x|+|y| Часто пишут xy вместо K(x,y) и x*y.

Определение

Пусть - некоторый алфавит. Для каждого x ^* и каждого натурального i определим i-ю итерацию xⁱ слова x как

xⁱ = xx^i-1 ,

где x⁰ = .

Пример

K(aabba, aaaaa) =aabbaaaaaa = a² b² a⁶=a² b² (aa)³ Введенное обозначение позволяет нам находить более короткое представление некоторых слов.

Определим подслова слова x как связанные части этого слова.

Связанные части слова

ab…..

bb………..c

ac……..b

подслово

ab…….b

b…….a

префикс

a……b

bb…ab

суффикс

Определение Пусть v,w ^* для некоторого алфавита . Тогда:

• v- подслово слова w x,y ^* : w=xvy;

• v- суффикс слова w x ^*: w=xv;

• v- префикс слова w y ^*:w=vy.

Определение Пусть x ^* и пусть a для некоторого алфавита .

Определим |x|_a как число вхождений символа а в x.

(посмотреть множества – мощность и множество всех подмножеств)

Пример

|(abbab)|_a =2 и |(11bb0)|₀ =1

Для каждого x ^* |x|= _a

Для практической работы с языками надо помнить, что в принципе языки суть множества, поэтому для них можно использовать стандартные операции объединения и пересечения множеств. Сюда можно добавить конкатенацию и звезду Клини.

Определение: Язык над алфавитом -это некоторое подмножество ^* . Дополнение L^C языка L относительно -это язык ^* _{_}- L.

L₀=0 – пустой язык

L ={ } –язык, содержащий единственное слово - пустое слово.

Если L₁ и L₂ - языки над алфавитом , то L₁*L₂=L₁L₂={ vw | v L₁, w L₂}

Это конкатенация языков L₁ и L₂.

Пусть L – некоторый язык над алфавитом . ( то есть язык есть некоторое множество слов над заданным алфавитом). Определим

L⁰:=L ,

Lⁱ⁺¹=Lⁱ*L для всех i N_0,

L^*= - звезда Клини языка L

L⁺= ₌ L*L^*

Примеры языков над алфавитом ={a,b}:

L1=0;

L2={ };

L3= { ,ab,abab};

L4= ^* = { ,a,b,aa,bb,…..};

L5= ⁺ ={a,b,aa,bb,….};

L6={a}^* ={ ,a,aa,aaa,……}={aⁱ : i N₀}

L7= ³ ={aaa,aab,aba,abb,baa,bab,bba,bbb}

Все грамматически правильные тексты (английские) и множество всех синтаксически правильных программ на ЯВУ – всегда некоторый язык над алфавитом _keyborard .

Замечание

Законы дистрибутивности относительно объединения и конкатенации выполняются:

Лемма: Пусть L_1,L₂ и L₃ - языки над алфавитом . Тогда

L₁ L₂ L₁ L₃=L₁ (L2 L₃)

Но закон дистрибутивности для конкатенации и пересечения не выполняется.

Лемма: пусть L₁,L₂ и L₃ -языки над алфавитом . Тогда

L₁(L₂ L₃) L₁L₂ L₁L₃

Вы видите, что вместо дистрибутивного закона выполняется только соответствующее включение. Достаточно указать три конкретных языка U₁, U₂,U₃, таких, что

U₁(U₂ U₃) U₁U₂ U₁U₃ . ( обдумать док-во)

Алгоритмические проблемы.

(Проблема принадлежности, проблема существования Гамильтонова цикла( HC), проблема выполнимости, оптимизационная проблема)

Если рассматривать алгоритм как программу, то для решения алгоритмических проблем нам безразличен выбор конкретного языка программирования. Мы просто хотим, чтобы программа вычисляла правильный выход для любого входа. Таким образом, алгоритм можно рассматривать как программу, заканчивающую работу для любого входа ( то есть не имеющую бесконечных вычислений) и решающую данную проблему. Тогда, любая программа ( алгоритм) выполняет отображение

А : ^* ₁ -> ^*₂ для некоторых алфавитов ₁ и ₂ .

Это значит, что:

- входы представлены как слова над алфавитом ₁;

- выходы представлены как слова над алфавитом ₂;

- А однозначно определяет выход по каждому входу.

Для некоторого алгоритма А и входа x обозначим записью A(x) выход алгоритма А для этого входа. Два алгоритма (программы) A и B эквивалентны, если они работают над одним и тем же алфавитом , и при этом A(x) =B(x) для всех x ^*.

Проблема принадлежности

Определение: для заданных алфавита и языка L ^* проблема принадлежности ( , L) заключается в том, что для любого x ^* необходимо ответить на вопрос, какое именно условие из следующих двух выполнено :

x L или x L.

Алгоритм А решает проблему принадлежности (L, ), если для всех x ^* выполнено следующее:

A(x)= 1, если x L

0, если x L.

тогда говорят, что А распознает язык L.

Если есть алгоритм для некоторого языка L, который распознает L,то говорят, что язык L является рекурсивным.

Проблема принадлежности ( , L)описывается так:

( , L)

Вход : x ^*.

Выход : A(x) _bool={0,1}, где

A(x)= 1,если x L (да)

0, если x L (нет)

Пример

({a,b}, {aⁿbⁿ} | n N₀

Вход: x {a,b}^*

Выход : Да, если x=aⁿ bⁿ для некоторого n N₀

Нет – в противном случае.

Сложность по Колмогорову

Как измерить количество информации в словах?

Что такое колмогоровская сложность?

Все мы архивировали свои файлы (arj, rar, zip, bи т.д.). Это происходит с помощью программ, которые сжимают эти файлы. Применив такую программу к некоторому файлу, содержащему текст или программу , мы на выходе получаем его сжатую версию. Она ,как правило, короче исходного файла. По ней можно восстановить исходный файл.

В первом приближении колмогоровскую сложность можно описать как длину его сжатой версии. И тогда файл, имеющий регулярную структуру и хорошо сжимаемый, имеет малую колмогоровскую сложность (в сравнении с его длиной). Наоборот, плохо сжимаемый файл имеет сложность, близкую к длине.

Мы будем рассматривать только слова над булевским алфавитом _bool . и измерять информацию следующим образом. Будем считать, что слово w содержит мало информации, если есть короткое представление этого слова( то есть если оно сжимаемое) .

Слово содержит много информации, если не существует короткого представления w. (то есть такого представления, которое было бы короче, чем |w|). Интуитивно ясно, что слово с малым информационным содержанием является регулярным, и значит, его можно легко описать. Слово с высоким информационным содержанием нерегулярно (то есть является случайным распределением нулей и единиц) Поэтому такое слово приходится записывать постепенно, бит за битом.

Пример