Выводы:

1. Есть ли такие задачи, которые не могут быть решены на компьютере вне зависимости от его вычислительной мощности?

Да, такие задачи есть.

Теорема Геделя о неполноте.

Примеры алгоритмически неразрешимых проблем

2.Как определить, какие проблемы являются алгоритмически неразрешимыми ?

Теория вычислимости

3. Если задача алгоритмически разрешима, то насколько сложна может быть эта задача?

Теория сложности

4. Есть специальные разделы теоретической информатики, занимающиеся случайными процессами (рандомизация).

Теория вероятностей

5. Есть широкий круг вопросов, связанных с распределенными вычислениями.

Коммуникационные протоколы, сетевые модели.

Иначе это можно сказать так:

• При исследовании некоторой задачи результаты теории алгоритмов позволяют ответить на вопрос – является ли эта задача в принципе алгоритмически разрешимой.

• Для алгоритмически неразрешимых задач возможно их сведение к задаче останова машины Тьюринга.

• Мы имеем возможность получения оценок скорости роста сложности алгоритмов.

Существует классификация скорости роста сложности алгоритма, которая определяется старшим членом формулы. Младшими членами, которые растут медленно, можно пренебречь. Например, если мы установили при анализе алгоритма, что он делает x³ - 10x сравнений, то можно говорить, что сложность алгоритма растет как x³. Потому что, если входных данных будет >=100, то разница между x³-10x и x³ составляет меньше 0,3%.

Алгоритмы можно сгруппировать по скорости роста их сложности.

Класс функций (f) . (омега большое)

Функция g принадлежит этому классу, если при всех значениях аргумента n , больших некоторого порога n_o значение g(n) > c*f(n) для некоторого положительного числа с. Класс задается указанием своей нижней границы. А это значит, что в класс (n²) входят все функции, растущие быстрее, чем n² ( n³ или 2ⁿ ).Этот класс мало интересен, если мы занимаемся эффективностью алгоритма.

Класс функций O(f) ( О большое)

Этот класс состоит из функций, растущих не быстрее f .Функция f образует верхнюю границу для класса. Функции g принадлежит классу О(f), если g(n) <= c*f(n) для всех n, больших некоторого порога n₀ , и для некоторой положительной константы с. Это важно для нас. У нас есть два алгоритма. Принадлежит ли сложность первого из них классу О большое от сложности второго. Если окажется, что это так, значит, второй алгоритм не лучше первого решает поставленную задачу.

Класс (f) (тета большое)

Это класс функций, растущих с той же скоростью, что и f. Этот класс представляет собой пересечение двух предыдущих классов,

(f) = (f) O(f)

При сравнении алгоритмов нас будут интересовать такие, которые решают задачу быстрее, чем уже изученные. Алгоритмы этого класса не очень интересны.

Самый для нас интересный класс О. Проверить принадлежность функции классу О(f) можно либо с помощью данного выше определения, либо так:

g O(f), если = c для некоторой константы с.

Это означает, что если предел отношения g(n)/f(n) существует и он меньше бесконечности, то g O(f). Это не просто проверить для некоторых функций. В таких случаях по правилу Лопиталя (раскрывающего неопределенности вида ноль на ноль или бесконечность на бесконечность) можно заменить предел самих функций пределом их производных.

Каждый из классов является множеством, поэтому имеет смысл выражение “g – элемент этого множества”. И когда мы пишем g=O(f) , то это значит g O(f).

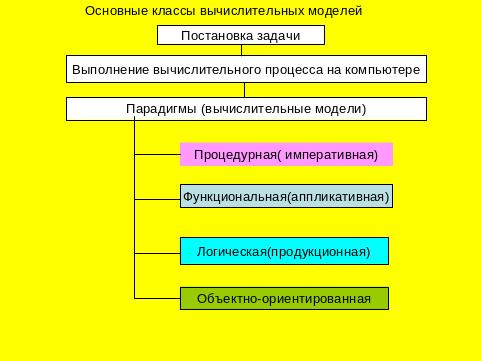
Различные стили программирования

Процедурная вычислительная модель

В этой модели алгоритм (программа) в явном виде (с помощью выполняемых операторов присваивания) определяет как сами действия, так и последовательность их выполнения ( С, С++, Pascal, Ada и другие языки программирования) Концепция памяти – преобразование исходного состояния памяти (значения переменных) в заключительное состояние. Фон-неймановские машины состоят из ячеек памяти и процессора, имеющего локальную память в виде регистров. Компьютер работает на ограниченном множестве операций, и программист вынужден мыслить в терминах этого ограниченного множества операций.