
- •Методичний посібник
- •Приклад розв’язку задачі 7. Розрахунок вала на згин з крученням 59
- •Умови задач Задача №1. Визначення реакцій опор балки
- •Задача №3. Розрахунок на міцність і визначення переміщень при розтягу і стиску
- •Задача №4. Визначення осьових моментів інерції плоских перетинів
- •Задача №5. Розрахунок вала на кручення
- •Задача №6. Розрахунок на міцність при згині балок
- •Задача №7. Розрахунок вала на згин з крученням
- •Задача №8. Розрахунок на стійкість
- •Форма поперечного перетину стержня
- •Методичні вказівки до розв'язку задач
- •1.Статика
- •Аксіоми статики
- •В’язі та реакції в’язей. Принцип звільнення.
- •М омент сили відносно точки
- •Пара сил і момент пари
- •Умови рівноваги плоскої системи сил
- •Приклад розв’язку задачі 1 визначення реакцій опор балки
- •Розв’язання
- •Приклад розв’язку задачі 2 визначення реакцій защемлення
- •Розв’язання
- •2. Центральний розтяг-стиск
- •Розв’язання
- •Розглянемо деформацію стержня навантаженого осьовою силою f (рис. 2.3):
- •3. Геометричні характеристики плоских перетинів
- •Приклад розв'язку задачі 3 визначення моментів інерції плоских перетинів
- •Розв’язання
- •4. Розрахунок вала на кручення
- •Приклад розв’язку задачі 4 розрахунок вала на міцність і жорсткість
- •Розв’язання
- •5. Прямий поперечний згин
- •Приклади побудови епюр поперечних сил та згинальних моментів
- •Контроль правильності побудови епюр
- •Приклад розв'язку задачі 5 розрахунок балки на міцність
- •Розв’язання
- •6. Сумісна дія згину з крученням
- •Приклад розв’язку задачі 6 розрахунок вала на згин з крученням
- •Розв’язання
- •7. Стійкість центрально стиснутих стержнів
- •Приклад розв’язку задачі 7 підбір поперечного перетину стояка
- •Розв’язання
- •Список рекомендованої літератури
3. Геометричні характеристики плоских перетинів
Статичні моменти площі довільної форми (рис. 3.1) визначають за формулами:
![]() ;
; ![]()
або
![]() ;
; ![]() ;
;
де
![]() – координати центра ваги перетину;
– координати центра ваги перетину;
– площа перетину.

Рис. 3.1
Дана властивість використовується для визначення центра ваги складних поперечних перетинів:
![]() ;
; ![]() ;
;
де
![]() – сума статичних моментів елементарних
площ;
– сума статичних моментів елементарних
площ;
![]() – сума елементарних
площ.
– сума елементарних
площ.
Осі, що проходять через центр ваги перетину називаються центральними осями. Статистичний момент площі відносно центральної осі дорівнює нулю.
Полярний момент
інерції
поперечного перетину визначають за
інтегралом
![]() .
.
Полярний момент опору поперечного перетину відповідно
![]()
де
![]() –
координата точки перетину максимально
віддаленої точки від полюса.
–
координата точки перетину максимально
віддаленої точки від полюса.
Знайдемо ці характеристики для перетинів:
круг

![]()
![]()
кільце
![]()
де
 ;
;
![]()
Осьові моменти інерції поперечних перетинів визначають за інтегралами:
![]() ;
;
![]()
Осьові моменти опору поперечних перетинів визначають за формулами:
![]() ;
;
![]() ;
;
де
![]() ,
,![]() – координати точок перетину максимально
віддалених від осей X
та Y.
– координати точок перетину максимально
віддалених від осей X
та Y.
Визначимо ці характеристики для перетинів:
- круг

- прямокутник
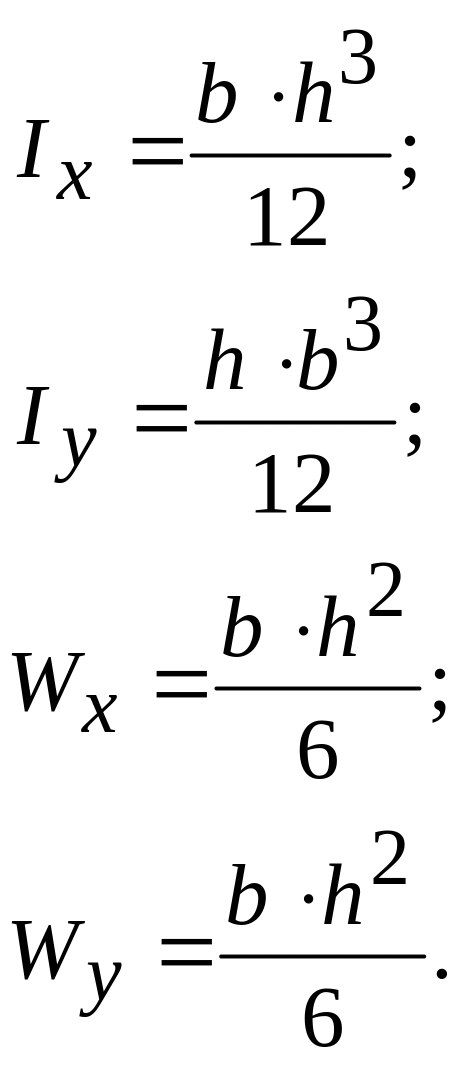
Залежність між моментами інерції при паралельному переносі осей
![]() .
.
Осьовий момент
інерції відносно будь-якої осі
![]() дорівнює осьовому моменту інерції
відносно центральної осі
,
яка паралельна осі
дорівнює осьовому моменту інерції
відносно центральної осі
,
яка паралельна осі
![]() ,
плюс добуток площі на квадрат відстані
між осями.
,
плюс добуток площі на квадрат відстані
між осями.
Приклад розв'язку задачі 3 визначення моментів інерції плоских перетинів
Для заданої плоскої фігури (рис. 3.2) визначити положення головних центральних осей інерції, величини осьових моментів інерцій та осьових моментів опору відносно них, якщо двотавр №33.
Розв’язання
Виписуємо геометричні характеристики вказаного прокатного профілю, двотавра № 33; позначаємо їх індексом 1.
Двотавр №33 (ГОСТ 8239-72)
h1 = 330мм; b1 = 140мм; d1 = 7,0мм; t1 = 11,2мм;
A1 = 53,8см2 ; IХ1 = 419см4; IУ1 = 9840см4 .
Визначаємо геометричні характеристики полоси.
Розміри полоси (позначимо індексом 2):
![]()
![]() .
.
Площа поперечного перетину полоси
![]()
Осьові моменти інерцій полоси:
![]()
![]()
Викреслюємо розрахункову схему в масштабі (рис. 3.2).

Рис. 3.2
Визначаємо координати центра ваги складного поперечного перетину в системі координат Y1 X1
![]() ;
;
![]()
де YC1 – відстань від центра ваги площі першої фігури (двотавра)
до осі Х1, YC1=0;
YC2 – відстань від центра ваги площі другої фігури (полоси);
YC2
=
![]() .
.
Підставимо значення і одержимо
![]()
Проводимо центральні осі YX (див. рис. 3.2).
Визначаємо осьові моменти інерції відносно головних центральних осей:
![]()

Визначаємо осьові моменти опору відносно центральних осей:
![]()
![]()
де
![]() ,
,
![]() – координати точок поперечного перетину
максимально віддалені від осей
– координати точок поперечного перетину
максимально віддалені від осей
![]() та
та
![]() (див. рис.
3.2):
(див. рис.
3.2):
![]()
![]()
