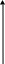Тема 3. Принципы управления электроприводами. Регуляторы.
Требования к следящему приводу
Работоспособность САУ ЭП определяется устойчивостью (сигнал рассогласования (W-X) со временем должен стремиться к нулю)
Качество регулирования определяется:
точностью (статической погрешностью);
временем успокоения;
максимальной динамической погрешностью;
диапазоном регулирования (Ymac / Ymin).
Рассмотрим уравнение движения ротора:
(3.1)
или в координатах:
(3.2)
где kвт момент вязкого трения;
J – момент инерции ротора;
Мэ – электромагнитный момент нагрузки;
Ма = const – момент активный нагрузки;
- частота вращения.
(3.3)
Следящий привод с П – регулятором.
Рассмотрим привод с пропорциональным управлением.
Подставим пропорциональное управление: Мэ = Ку Y
Y – управляющая функция регулятора
Ky – коэффициент управления
С учетом Y =W – X, откуда выразив X = W – Y, получим:
(3.4)
Имеем линейное дифференциальное уравнение второго порядка. Решаем классическим методом. Его решение имеет вид:
Y(t) = A1*eλ1t + A2*eλ2t,
где λ – корни характеристического уравнения.
Для отыскания λ составим характеристическое уравнение:
J*λ2 - KВТ*λ – Ky = 0
Его решение:
(3.5)
Характер изменения сигнала управления в переходном режиме определяется значениями корней характеристического уравнения. Для устойчивости привода необходимо и достаточно, чтобы λ<0.
Статистическая
погрешность определяется величиной Ма
– активного момента,
.
Частота затухающих колебаний:
(3.6)
Добротность системы определяется отношением X к установившейся ошибке: YУСТ: D = X/YУСТ.
Степень успокоения:
(3.7)
Следящий привод с Д-регулятором.
В таком приводе Мэ определяется:
(3.8)
Анализ проводим аналогичным образом, как и в предыдущем случае. Введение в следящий привод Д-регулятора повышает устойчивость, так как увеличивает коэффициент демпфирования.
Следящий привод с И-регулятором.
В таком приводе Мэ определяется:
(3.9)
Анализ проводим аналогичным образом, как и в предыдущем случае. Особенностью является то, что введение И-регулятора повышает порядок уравнения до третьего. В этом случае, имеем три корня – возможное их расположение:
а) все три корня действительные и отрицательные – система устойчива, апериодическая;
б) все три корня имеют отрицательные действительные части – система устойчива колебательно;
в) один или более корней с положительной действительной частью – система неустойчива.
Тема 4. Согласование частотных характеристик двигателя с типом нагрузки.
4.1. Типы нагрузки. По характеру зависимости Mн = Mн(Ω) нагрузку можно разделить как показано в таблице 13.1.
Таблица 13.1
Тип нагрузки (частотная зависимость) |
Момента |
Мощности |
С постоянной мощностью |
Mн=k Ω-1 |
Pн=const |
С постоянным моментом |
Mн=const |
Pн=k Ω |
«вентиляторной» нагрузкой |
Mн=k Ω |
Pн= k Ω2 |
4.2. Условие согласования механической характеристики двигателя и типа нагрузки.
Из уравнения баланса вытекает, что при любом способе регулирования важен характер зависимости Mc=f(ω) и величина скольжения.
В регулируемых электроприводах все эти зависимости можно реализовать и для электромагнитных моментов.
Наиболее просто осуществляется управление при постоянстве мощности или момента. Поэтому, если Mc=const, а регулирование частоты вращения осуществляется при Pд=const, то во всем диапазоне регулирования ∆ω будет недоиспользована мощность двигателя (рис.3а).
Если же для рабочей машины, работающей в режиме Рс = const применить привод, работающий в режиме Mд=const, то двигатель также будет недогружен в диапазоне ∆ω (рис.13).
Mc= k ω-1 (Рс = const) Mд=const |
Mc=const,Рс = const Mc=k ω-1 Pд=const |
Mc=k ω-1 Mc=const, Pд=const |
|
|
|
рис.13.
И тот и другой вариант несоответствия зависимостей Mд(ω) и Мс(ω) приводит к экономическим потерям. Поэтому при оценке регулировочных свойств привода учет этих соображений является обязательным.
Необходимо также учитывать, что режимы регулирования частоты вращения связаны с длительным отклонением параметров, определяющих режим работы машины, от номинальных значений и, следовательно, такие энергетические показатели как КПД, коэффициент мощности, потери энергии приобретают первостепенное значение.