
- •4. Методы аналитической геометрии в 3-х мерном эвклидовом пространстве
- •4.1. Декартовы координаты
- •Геометрические свойства смешанного произведения:
- •4.2. Плоскость в пространстве
- •4.3. Взаимное расположение в пространстве двух плоскостей:
- •4.4. Прямая в пространстве. Уравнение прямой.
- •Прямая и плоскость в пространстве
4.3. Взаимное расположение в пространстве двух плоскостей:

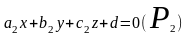
определяется
их нормальными векторами
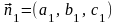 и
и
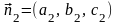 .
.
1) Углом между плоскостями a1x + b1y + c1z + d1 = 0 и a2x + b2 y + + c2 z + d2 = 0 называется угол , образованный векторами нормалей и к этим плоскостям:
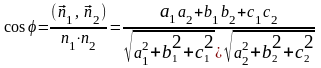 .
.
2)
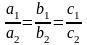 – условие параллельности плоскостей
a1x + b1
y + c1
z +
+ d1 = 0
и a2
x + b2 y + c2 z + d2 = 0.
– условие параллельности плоскостей
a1x + b1
y + c1
z +
+ d1 = 0
и a2
x + b2 y + c2 z + d2 = 0.
a1a2 + b1b2 + c1c2 = 0 – условие перпендикулярности плоскостей a1x + b1y + c1z + d1 = 0 и a2x + b2y + c2z + d2 = 0.
Это
условие может быть записано в более
компактном виде:
 ,
где
,
где
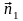 и
и
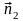 векторы нормалей к соответствующим
плоскостям.
векторы нормалей к соответствующим
плоскостям.
Пример 4.11. Найти угол между плоскостями x + 2y – 2z + 5 = 0 и x + y – 9 = 0.
Решение.
Так как
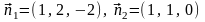 ,
,
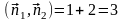 ,
,
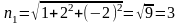 ,
,
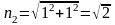 ,
,
то
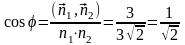 .
.
Следовательно,
угол между плоскостями
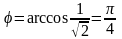 .
.
Пример 4.12. Написать уравнение плоскости, проходящей через точку А(–1, 3, 5) параллельно плоскости 3x + 2y – z – 5 = 0.
Решение.
Вектор нормали заданной плоскости
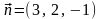 ,
очевидно, будет вектором нормали и
искомой плоскости. Поэтому, используя
уравнение плоскости, проходящей через
данную точку, получаем:
,
очевидно, будет вектором нормали и
искомой плоскости. Поэтому, используя
уравнение плоскости, проходящей через
данную точку, получаем:
3(x + 1) + 2(y – 3) – 1(z – 5) = 0
 3x + 3 + 2y – 6 – z + 5 = 0
3x + 3 + 2y – 6 – z + 5 = 0
3x + 2y – z + 2 = 0 – уравнение искомой плоскости.
4.4. Прямая в пространстве. Уравнение прямой.
Множество
точек
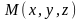 в трехмерном пространстве, координаты
которых удовлетворяют системе уравнений
в трехмерном пространстве, координаты
которых удовлетворяют системе уравнений
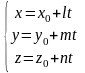
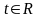 (4.7)
(4.7)
называется
прямой, проходящей через точку
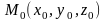 и параллельной
вектору
и параллельной
вектору
 .
Вектор
.
Вектор
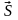 называется направляющим вектором
данной прямой, переменная величина
называется направляющим вектором
данной прямой, переменная величина
 ,
,
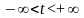 ,
называется параметром, а система
(4.7) называется параметрическим
уравнением прямой в пространстве.
Параметр
выражается линейно через текущие
координаты
,
называется параметром, а система
(4.7) называется параметрическим
уравнением прямой в пространстве.
Параметр
выражается линейно через текущие
координаты
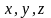 точки
точки
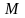 ,если
,если
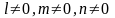 :
:

Каноническими
уравнениями прямой называют линейные
зависимости между координатами точки
 ,
расположенной на прямой:
,
расположенной на прямой:
 . (4.8)
. (4.8)
Известно
из геометрии, что через две точки
 и
и
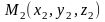 можно провести только одну прямую.
Найдем уравнение этой прямой. Очевидно,
прямая проходит через точку
параллельно вектору
.
По формуле (4.8) уравнение прямой, проходящей
через две точки
можно провести только одну прямую.
Найдем уравнение этой прямой. Очевидно,
прямая проходит через точку
параллельно вектору
.
По формуле (4.8) уравнение прямой, проходящей
через две точки
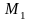 и
и
 имеет вид:
имеет вид:
 (4.9)
(4.9)
Прямую
можно рассматривать как пересечение
двух плоскостей
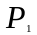 и
и
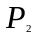
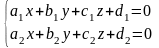 (4.10)
(4.10)
Эта система называется общими уравнениями прямой.
Направляющий
вектор
этой прямой перпендикулярен нормальным
векторам
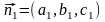 и
и
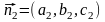 плоскостей
и
.
Поэтому, можно выбрать в качестве
направляющего вектора векторное
произведение нормальных векторов
плоскостей:
плоскостей
и
.
Поэтому, можно выбрать в качестве
направляющего вектора векторное
произведение нормальных векторов
плоскостей:
 .
Координатами точки
на прямой может служить любое частное
решение системы (4.10). Таким образом, по
общим уравнениям прямой (4.10) можно
составлять канонические уравнения
прямой
.
Координатами точки
на прямой может служить любое частное
решение системы (4.10). Таким образом, по
общим уравнениям прямой (4.10) можно
составлять канонические уравнения
прямой
Заметим, что из каждого вида уравнений прямой в пространстве можно получить любой другой вид уравнений прямой в пространстве.
Пример
4.13. Написать уравнения прямой, проходящей
через точку А(2,-1,4) параллельно вектору
 в параметрической и канонической формах.
в параметрической и канонической формах.
Решение. Параметрическое уравнение прямой имеет вид:

Канонические
уравнения прямой имеют вид:
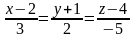 .
.
Пример 4.14. Написать уравнения прямой, проходящей через точку А (– 3, 1, 2) параллельно прямой:
а)  ;
б)
;
б)  в)
в) 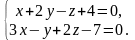
Решение.
а) Направляющий вектор заданной прямой
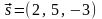 ,
очевидно, является направляющим вектором
искомой прямой. Поэтому:
,
очевидно, является направляющим вектором
искомой прямой. Поэтому:
 – искомое уравнение.
– искомое уравнение.
б)
Направляющий вектор заданной прямой
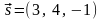 .
Следовательно, уравнения искомой прямой
.
Следовательно, уравнения искомой прямой
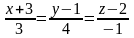 .
.
в)
Направляющим вектором искомой прямой
будет вектор
 ,
где
,
где
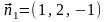 и
и
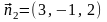 – векторы нормалей к плоскостям
x + 2y – z + 4 = 0
и 3x – y + 2z – 7 = 0.
– векторы нормалей к плоскостям
x + 2y – z + 4 = 0
и 3x – y + 2z – 7 = 0.
Тогда
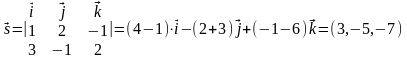 .
.
Поэтому,
уравнения искомой прямой:
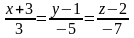 .
.
Пример 4.15. Написать уравнения прямой, проходящей через точки А(2, 3, – 5) и В (– 3, 1, 4).
Решение.
Используя уравнения прямой, проходящей
через две точки получаем:
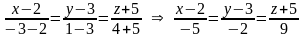 .
.
Пример 4.16. Написать канонические уравнения прямой
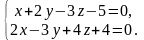
Решение. Найдем направляющий вектор данной прямой
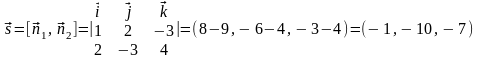 .
.
Чтобы написать канонические уравнения прямой необходимо еще найти какую-нибудь точку на этой прямой. В качестве такой точки А(x0, y0, z0) возьмем, например ту, у которой z0 = 0, т. е. А(x0, y0, 0). Тогда ее координаты x0 и y0 обязаны удовлетворять уравнениям:
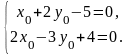
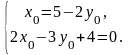
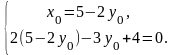
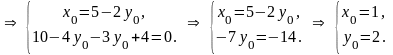
Следовательно, точка А(1, 2, 0) принадлежит заданной прямой. Теперь напишем канонические уравнения этой прямой:
 .
.
Расстояние от точки до прямой в пространстве
Расстояние δ от точки М1(х1, y1, z1) до прямой L:
равно длине перпендикуляра М1М2, проведенного из точки М1 на прямую L (рис. 4.7).
Отрезок
М1М2
является высотой параллелограмма,
построенного на векторах
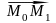 и
с общим началом в точке М0(х0,
y0,
z0).
и
с общим началом в точке М0(х0,
y0,
z0).
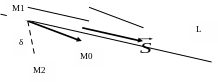
Рис. 4.7. Расстояние от точки до прямой
Площадь
этого параллелограмма с одной стороны
равна произведению высоты на основание:
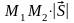 ,
а с другой – по свойству векторного
произведения
,
а с другой – по свойству векторного
произведения
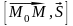 - его длине:
- его длине:
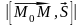 .
Отсюда:
.
Отсюда:
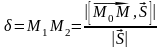 ;
;
 (4.11)
(4.11)
Пример 4.17. Найти расстояние от точки A(4; 4; 4) до прямой L, заданной каноническими уравнениями
![]() .
.
Решение.
1
способ. Запишем параметрические уравнения
прямой L
с начальной точкой P(4;
5; 8) и направляющим вектором
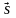 = (1; 2; 3):
= (1; 2; 3):
x = 4 + t, y = 5 + 2t, z = 8 + 3t.
Таким образом, проекция точки A на прямую L имеет вид
B(4 + t, 5 + 2t, 8 + 3t).
Чтобы найти t, необходимо воспользоваться условием ортогональности векторов и .
Имеем
( , ) = ((1; 2; 3), (t, 1 + 2t, 4 + 3t)) = t + 2 + 4t + 12 + 9t = 14 + 14t = 0.
Отсюда t = −1, B = (3; 3; 5), = (−1, −1, 1). Окончательно, имеем
 .
.
2 способ. По формуле (4.11) получаем:
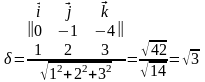 .
.
Скрещивающиеся прямые
Найдем расстояние между двумя скрещивающимися прямыми L1 и L2:
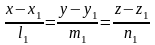 ,
,
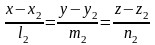 .
.
Расстоянием между прямыми называют длину общего перпендикуляра.
Геометрическое построение общего перпендикуляра начнем с простого примера двух параллельных прямых L1 и L3 (рис. 4.8) :
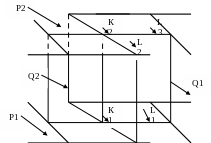
Рис. 4.8. Прямые: параллельные и скрещивающиеся
Возьмем любую точку К1 на прямой L1 и в плоскости, проходящей через параллельные прямые L1 и L3, проведем перпендикуляр К1К2 к прямой L3. Это общий перпендикуляр к прямым L1 и L3 в силу их параллельности.
Будем
считать, что прямые L1
и
L3
расположены
в параллельных плоскостях Р1
и
Р2,
проходящих
через точки К1
и
К2,
перпендикулярно вектору
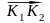 .
Проведем в плоскости Р2
через
точку К2
прямую L2,
пересекающую
прямую L3
.
Тогда К1К2
-
общий перпендикуляр скрещивающихся
прямых L1
и
L2.
Заметим, что длина перпендикуляра К1К2
равна
расстоянию между параллельными
плоскостями Р1
и
Р2.
Уравнение прямой К1К2
задается
пересечением плоскостей Q1
и
Q2,
проходящих
через прямые L1
и
L2,
перпендикулярно
плоскостям
Р1
и
Р2.
.
Проведем в плоскости Р2
через
точку К2
прямую L2,
пересекающую
прямую L3
.
Тогда К1К2
-
общий перпендикуляр скрещивающихся
прямых L1
и
L2.
Заметим, что длина перпендикуляра К1К2
равна
расстоянию между параллельными
плоскостями Р1
и
Р2.
Уравнение прямой К1К2
задается
пересечением плоскостей Q1
и
Q2,
проходящих
через прямые L1
и
L2,
перпендикулярно
плоскостям
Р1
и
Р2.
Теперь рассмотрим любые две скрещивающиеся прямые L1 и L2. Сначала построим их общий перпендикуляр.
Проведем плоскость Р1 через прямую L1 параллельно прямой L2 и плоскость Р2 - через прямую L2 параллельно прямой L1. Направляющие векторы прямых и образуют направляющее векторное пространство параллельных плоскостей Р1 и Р2.
Далее, через прямую L1 и прямую L2 проведем плоскости Q1 и Q2, перпендикулярные плоскостям Р1 и Р2. Прямая, задаваемая пересечением плоскостей Q1 и Q2, перпендикулярна параллельным плоскостям Р1 и Р2. Отрезок К1К2, заключенный между плоскостями Р1 и Р2, является общим перпендикуляром скрещивающихся прямых L1 и L2. Его длина равна как расстоянию между прямыми L1 и L2, так и расстоянию между плоскостями Р1 и Р2.
Для
нахождения длины общего перпендикуляра
прямых L1
и
L2
построим параллелепипед по трем векторам
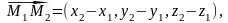
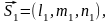 с общим началом в точке М1.
с общим началом в точке М1.
Основание
параллелограмма с вершиной в точке М1
расположено в плоскости Р1,
а основание с вершиной в точке М2
в плоскости Р2.
Оба основания построены по векторам
и
.
Поэтому площадь параллелограмма в
основаниях равна длине вектора
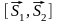 :
:
 .
.
Объем
параллелепипеда определим по смешанному
произведению векторов
 ,
и
.
,
и
.
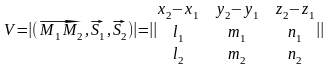 .
.
Расстояние
между плоскостями Р1
и
Р2
равно высоте рассмотренного выше
параллелепипеда и может быть вычислено
по формуле
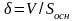 .
.
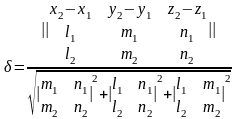 .
.
Уравнения общего перпендикуляра скрещивающихся прямых задаются пересечением плоскостей Q1 и Q2, проходящих соответственно через прямые L1 и L2 перпендикулярно параллельным плоскостям Р1 и Р2 :

(Уравнение плоскости Q2)

Направляющими
векторами плоскостей Q1
и
Q2,
соответственно, являются пары
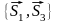 и
и
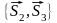 ,
где
,
где
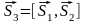 - нормальный вектор плоскостей Р1
и
Р2
.
- нормальный вектор плоскостей Р1
и
Р2
.
Нормальные
векторы плоскостей Q1
и
Q2
определяются векторными произведениями
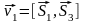 и
и
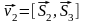 .
.
Пример 4.18. Составить уравнения общего перпендикуляра к скрещивающимся прямым
![]()
и найти расстояние между ними.
Решение.
Плоскость, параллельная обеим прямым, перпендикулярна вектору:
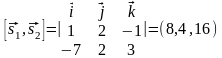 .
.
В качестве нормали этой плоскости можно взять вектор =(2; 1; 4) коллинеарный . Общий перпендикуляр к данным прямым представляет собой пересечение плоскостей
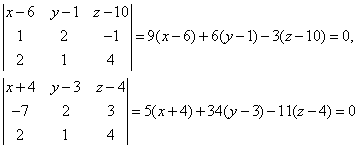
или, после упрощения,
3x − 2y − z − 6 = 0, 5x + 34y − 11z – 38 = 0.
Отсюда
получаем
 - уравнение общего перпендикуляра.
- уравнение общего перпендикуляра.
Далее,
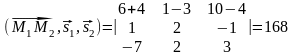 ,
,
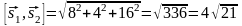 ,
,
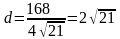 .
.
