- •4. Методы аналитической геометрии в 3-х мерном эвклидовом пространстве
- •4.1. Декартовы координаты
- •Геометрические свойства смешанного произведения:
- •4.2. Плоскость в пространстве
- •4.3. Взаимное расположение в пространстве двух плоскостей:
- •4.4. Прямая в пространстве. Уравнение прямой.
- •Прямая и плоскость в пространстве
4. Методы аналитической геометрии в 3-х мерном эвклидовом пространстве
4.1. Декартовы координаты
Будем
считать, что в пространстве введены
прямоугольные декартовы координаты.
Пусть О
(0;0;0) - начало координат
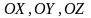 -
взаимно перпендикулярные оси ;
-
взаимно перпендикулярные оси ;
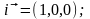
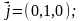
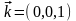 -
единичные орты этих осей.
-
единичные орты этих осей.
Найдем их скалярные произведения:
 ,
,
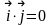 ,
,
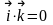 ,
,
 ,
,
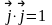 ,
,
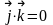 ,
,
 ,
,
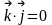 ,
,
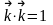 .
.
Таким
образом, векторы
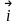 ,
,
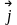 ,
,
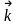 образуют ортонормированный базис,
поскольку
образуют ортонормированный базис,
поскольку
 и векторы
,
,
ортогональны. Этот базис мы будем
называть стандартным базисом пространства
R3.
и векторы
,
,
ортогональны. Этот базис мы будем
называть стандартным базисом пространства
R3.
Каждой
точке М(x,y,z)
соответствует радиус-вектор
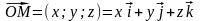 ,
каждой паре точек
,
каждой паре точек
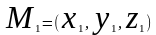 ,
,
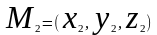 соответствует
вектор
соответствует
вектор
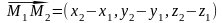 .
Если М1(х1,
у1,
z1)
и М2(х2,
у2,
z2)
– концы отрезка М1М2,
а точка М(х,
у,
z)
делит этот отрезок в отношении
.
Если М1(х1,
у1,
z1)
и М2(х2,
у2,
z2)
– концы отрезка М1М2,
а точка М(х,
у,
z)
делит этот отрезок в отношении
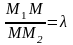 ,
то координаты этой точки:
,
то координаты этой точки:
 ;
;
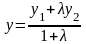 ;
;
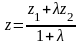 .
.
Если
М(х,
у,
z)
– середина отрезка М1М2,
то
 и
и
 ,
,
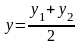 ,
,
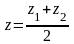 .
.
Любой
вектор обозначается двумя буквами
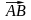 с чертой или стрелкой над ними, причем
первая буква указывает начало вектора,
а вторая – его конец. Вектор может быть
обозначен также одной буквой латинского
алфавита
с чертой или стрелкой над ними, причем
первая буква указывает начало вектора,
а вторая – его конец. Вектор может быть
обозначен также одной буквой латинского
алфавита
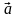 ,
,
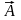 .
Длину или модуль вектора обозначают в
виде
.
Длину или модуль вектора обозначают в
виде
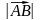 ,
|
|.
Вектор
может быть приложен к любой точке А
пространства.
,
|
|.
Вектор
может быть приложен к любой точке А
пространства.
Суммой
двух векторов
и
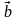 называется третий вектор
+
,
который идет из начала первого вектора
в конец второго
,
если второй вектор выходит из конца
первого (рис. 4.1)
называется третий вектор
+
,
который идет из начала первого вектора
в конец второго
,
если второй вектор выходит из конца
первого (рис. 4.1)

Рис. 4.1. Сложение векторов
Разностью двух векторов и называется третий вектор - , который представляет собой сумму вектора и вектора, противоположного вектору , т.е. - = + (- ) (рис. 4.2)

Рис. 4.2. Разность векторов
Произведением вектора на число λ называется вектор, обозначаемый λ , такой, что:
1) |λ | = |λ| | |;
2) векторы и λ имеют одно направление, если λ > 0, и противоположное, если λ < 0.
Если вектор составляет угол φ с осью Ох, то проекцией вектора на эту ось называется произведение модуля вектора на косинус угла φ:
прх = | | cos φ.
Проекция суммы векторов и на ось Ох равна сумме проекций этих векторов на эту ось:
прх ( + ) = прх + прх .
В трехмерном пространстве Oxyz вектор может быть представлен разложением по координатному базису в виде:
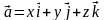 ,
,
где
 - единичные базисные векторы, направление
каждого из которых совпадает с
положительным направлением соответствующей
оси;
- единичные базисные векторы, направление
каждого из которых совпадает с
положительным направлением соответствующей
оси;
x, y, z – проекции вектора на оси координат.
Длина (модуль) вектора определяется через проекции по формуле:
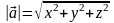 .
.
Косинусы углов α, β, γ, образованных вектором с осями координат, находятся в виде соотношений
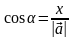 ,
,
 ,
,
 .
.
Они называются направляющими косинусами.
Равенство = (x, y, z) используется для выражения вектора через его проекции на заданные координатные оси.
Векторы, лежащие на одной прямой или параллельных прямых, называются коллинеарными. Условие коллинеарности двух векторов = (x1, y1, z1) и = (x2, y2, z2) записываются в виде:
= λ ,
где λ – числовой множитель.
Через координаты это условие записывается в виде:
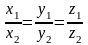 .
.
Для
каждой пары векторов
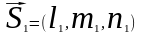 ;
;
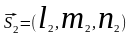 определены:
определены:
а)
скалярное
произведение:
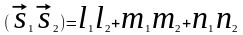
б)
длина вектора
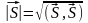 ,
где
,
где
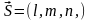
в) Углы между векторами вычисляются по формуле:
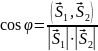
г) векторное произведение :
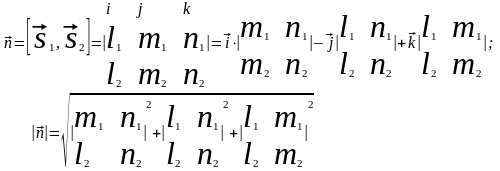
Свойства векторного произведения
векторов
 и
и
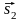 :
:

1) вектор
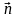 перпендикулярен каждому из векторов
и
;
перпендикулярен каждому из векторов
и
;
2) вектор
направлен так, что если смотреть с его
конца, то поворот первого вектора
ко второму вектору
на кратчайший угол
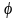 проходит против часовой стрелки;
проходит против часовой стрелки;
3) длина вектора
равна площади параллелограмма,
построенного на векторах
и
,
т.е.
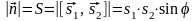 .
.
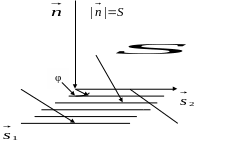
Рис. 4.3. Геометрический смысл векторного
произведения
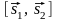
4) площадь треугольника, построенного
на векторах
и
,
равна
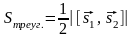 ;
;
5)
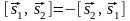 ,
,
6)
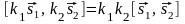 ,
,
7)
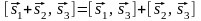 ,
,
8)
если векторы
и
коллинеарны, то
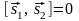 .
В частности,
.
В частности,
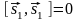 .
.
д)
смешанное
произведение трех векторов
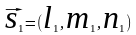 ,
,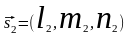 ,
,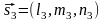 есть
число, обозначаемое
есть
число, обозначаемое