Структура продолжений двойственной пары

Дадим краткое описание рёберно-сетчатой модели. Ранее были отмечены характерные аспекты, которые учитываются при создании таких моделей. Например, построив рёберный додекаэдр, следует заняться оформлением его внутреннего пространства с помощью нитей. Во-первых, соединяются противоположные пары рёбер многогранника. Эти соединения образуют «золотые» прямоугольники. Противоположные пары рёбер додекаэдра являются малыми их сторонами. Тридцать больших сторон прямоугольников ограничивают фигуру икосаэдра внутри рёберного додекаэдра. Во-вторых, соединяются вершины противоположных граней додекаэдра и образуются из нитей рёбра шести его пятиугольных антипризм (рис. 33 а).

Рис. 33.

Следующий этап работы направляется на создание рёберных пятиугольных пирамид (рис. 33 б). Изображение (рис. 33 в) напоминает форму малого звёздчатого додекаэдра - одно из тел Кеплера - Пуансо. На предыдущем изображении (рис. б) видно, что продолженные рёбра додекаэдра отсекают у пространства равнобедренные треугольники. Пять треугольников образуют пятиугольную пирамиду.

Далее с помощью клея соединяются основания пирамид с рёберными гранями додекаэдра (рис. 33 в). Если исключить часть пятиугольных пирамид, относящихся к фигуре малого звёздчатого додекаэдра, то многогранник будет по форме напоминать пирамидальную конструкцию (рис. 34). В её внутреннем пространстве, оформленном нитями, выбираются элементы пространственных отсеков для построения макетов определённых форм (рис. 35).

В ПРИЛОЖЕНИИ (рис. 63 - 76) представлены образцы пирамидальных форм, моночертежей и развёрток.

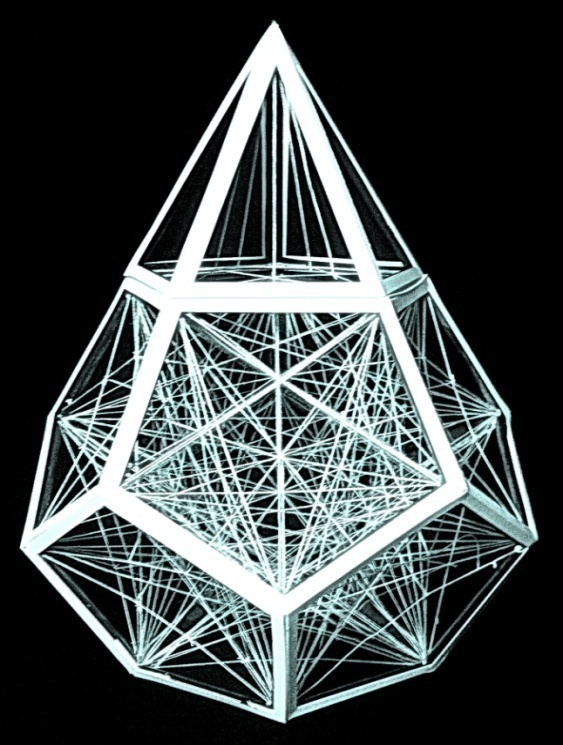
Рис. 34. Рис. 35.

Если каждую тройку вершин малого звёздчатого додекаэдра соединить, то образуются рёбра двадцатигранного икосаэдра. На рисунке 36 изображена рёберно-сетчатая модель икосаэдра с видом: «ребро», «грань» и «вершина». Красным цветом выделены большие стороны так называемых «золотых» прямоугольников. На рисунке 36а прямоугольник воспринимается неискаженно. Он лежит в экваториальной плоскости. Её проекция, изображенная на рисунке 24, ограничена квадратом ABCD и фигурой неправильного шестиугольника.

Рис. 36.

Наряду с различными геометрическими структурами, правильные многогранники (тела Платона) являются источником симметрии и «золотых» пропорций. В определённом смысле они напоминают формы кристаллов. Симметрии и правильность внешнего вида многогранников вызывает интерес к изучению их внутренней структуры. Удалением одной из граней, например, в бумажном макете икосаэдра, или рассечением его экваториальной плоскостью, обнаруживается внутри «пустота».

Древним грекам были известны пять правильных тел (тетраэдр, куб, октаэдр, додекаэдр и икосаэдр), которым они отводили роль элементарных «кирпичиков» материального мира. В отличие от геометрии правильных тел, красоте геометрических форм кристаллов свойственно так называемое прорастание. Естественно допустить, что продолжения многогранников, своеобразно «покрывают» образующие плоскости двухмерными отсеками. Они по законам симметрии как бы «прорастают» в трёхмерные формы. Такое развитие многогранного «ядра» задаётся продолжением плоскостей граней. Они взаимосвязаны с феноменом внутренней структуры геометрического тела. Такая реакция вызывается при ближайшем рассмотрении рёберно-сетчатых моделей.

Автор упомянутой книги «Геометрия дизайна» К.Элам, прослеживая пропорциональную организацию форм искусства и форм природы, подчеркивает: «Предпочтение, которое отдаётся золотому сечению, не связано с эстетическим взглядом человека, а является также частью поразительного соотношения форм роста живых организмов: растений и животных» (7 , с.10).

При ознакомлении со структурой внутреннего пространства рёберно-сетчатых моделей двойственной пары икосаэдра и додекаэдра, обнаруживаются различные отсеки вблизи двойника и в удалении от него - на периферии пересекающихся плоскостей. Продолжения одного из двойников - как бы промежуточный «рост» геометрической структуры и её переход в конфигурацию другого двойника. Такое чередование бесконечно в одном и противоположном ему направлении.

Равносторонний пятиугольник

Равносторонний пятиугольник часто встречается в структуре двойственной пары икосаэдра и додекаэдра. При построении данного многоугольника, в частности, «от руки» - с помощью циркуля и линейки, часто возникает заметная погрешность в размерах его сторон. Например, при делении окружности на пять равных частей геометрическим способом, или с применением коэффициента (l=dk), хорды не всегда согласуются размерами.

Каждый способ построения равностороннего пятиугольника по – своему уникален. Проще всего строить n-угольники, если использовать компьютер, например, программное приложение Corel DRAW. Следует лишь открыть меню объект, выбрать инструмент многоугольник (пятиугольник), щелкнуть и перетащить курсор в требуемое место - в окно рисования, определив нужный размер фигуры. Удерживанием нажатой клавиши Ctrl получают изображение равностороннего многоугольника. Чтобы задать число сторон или вершин при выборе многоугольника, то на соответствующей панели вводиться значение в поле число вершин или сторон многоугольника.

При создании развёрток для трёхмерного макетирования, не исключаются различные способы n-угольных фигур, в том числе и способ «от руки». Для получения равностороннего пятиугольника применим метод динамического прямоугольника .

Правильный пятиугольник закономерно разбивается собственными диагоналями, построение которых дают пентаграмму - пятиугольную звезду. Её центром является пятиугольник. Его вершины - точки сторон пентаграммы. Каждая точка делит соответствующую сторону пятиконечной звезды на два пропорциональных отрезка. Известно, что отношение более длинного отрезка к меньшему равно примерно 1. 618: 1, что прямо относится к «золотому сечению».

На рисунке 37а изображен прямоугольник ABCD . Его составляют два квадрата. Диагонали равны - гипотенузы прямоугольных треугольников.

На рисунке 37 б изображена схема построения двух прямоугольников на основе диагоналей DF и СF соответствующих квадратов. Получен пропорциональный прямоугольник NPCD.

Пересечение диагоналей дают точку H - вершину строящегося пятиугольника, а также две его стороны HC, HD и его диагональ CD (рис. 37 в).

На рисунке 38а изображена схема построения остальных сторон пятиугольника с помощью пересечения дополнительных дуг из точек C и D как из центров окружностей.

На диагонали CD (рис. 38б) две дуги задают точки 4, 5. Они делят диагональ пятиугольника в соответствии с «золотыми» пропорциями. На этой схеме выделены три фигуры, имеющие прямое отношение к двенадцатиграннику - додекаэдру. Фигура HCLKD - его пятиугольная грань, фигуры MRCD и SCD - n -угольники, ограничивающие малые диагональные плоскости сечения додекаэдра. На плоскости равностороннего треугольника SCD отражены следы продолжений двойственного икосаэдра.

Предложенные схемы пошагового построения правильного пятиугольника приводят нас к рёберно-сетчатым моделям двойственной пары - икосаэдра и додекаэдра. На схеме (ПРИЛОЖЕНИЕ, рис. 80) представлен моночертёж. То есть изображение многоугольных фигур, которые ограничивают диагональные плоскости сечения рёберно-сетчатой модели двойственной пары правильных многогранников.

Рис. 37.

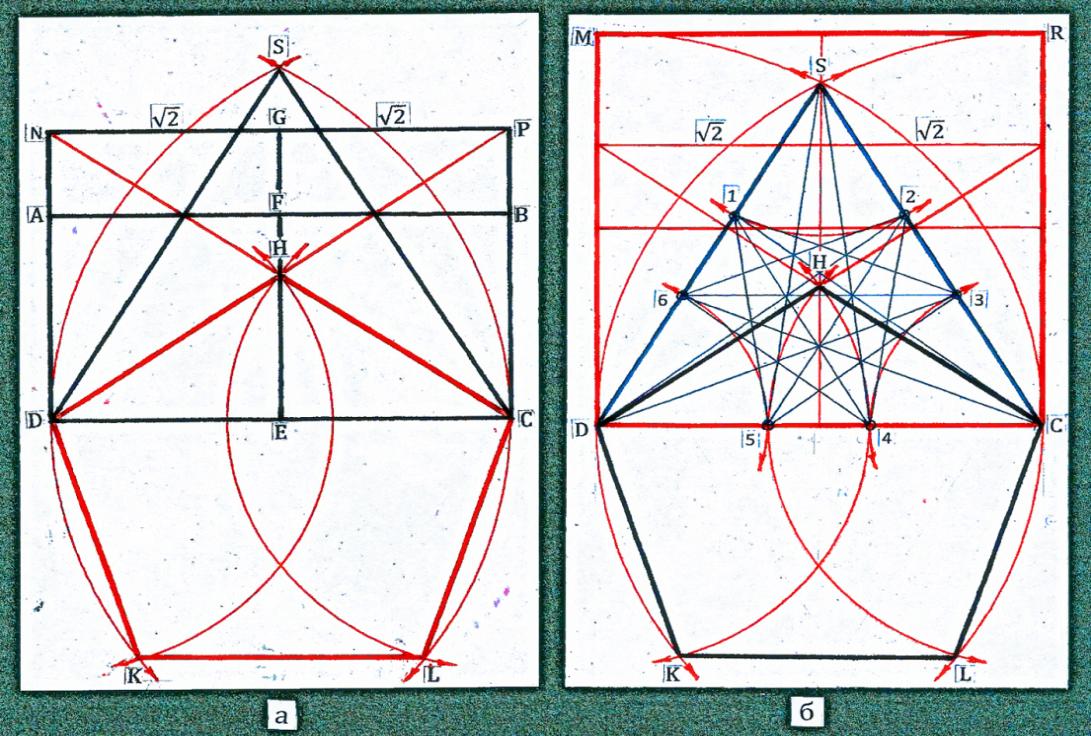
Рис. 38.