Раздел 1 геометрические тела. Многогранники

Многогранником называют геометрическое тело, ограниченное со всех сторон плоскими многоугольниками, которые называют гранями. Стороны граней - это рёбра многогранника, а концы его рёбер - вершины (10, с. 708).

Пять многогранников (тела Платона) - тетраэдр, куб, октаэдр, додекаэдр и икосаэдр, называют правильными выпуклыми. У каждого из них все грани одинаковые правильные многоугольники, а многогранные углы при вершинах равны (рис. 1, фигуры 1 – 5).

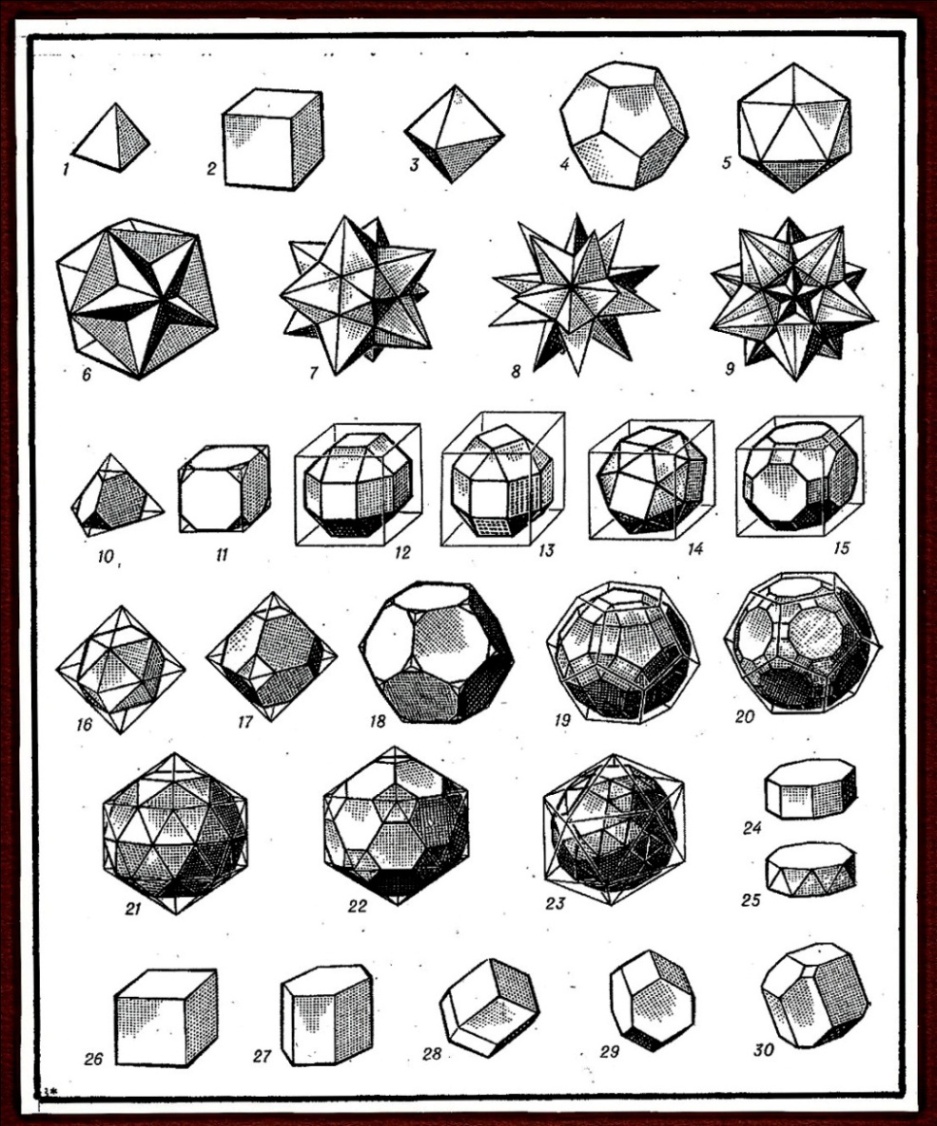
Рис. 1.

Четырнадцать многогранников (тела Архимеда) называют полуправильными выпуклыми многогранниками. Их многогранные углы (изогоны) равны, грани (изоэдры) - неодинаковые правильные многоугольники (фигуры 10 - 25).

Полуэдры (выпуклые многогранники) - геометрические тела. Ими можно заполнить «всё бесконечное пространство так, чтобы они не входили друг в друга и не оставляли пустот между собой, то есть образовали разбиение пространства» (фигуры 26 – 30).

Четыре правильные невыпуклые многогранники (тела Пуансо) - звёздчатые многогранники (фигуры 6 - 9).

Платон древнегреческий философ (427 – 347 гг. до н. э.), в своих трудах упомянул о тетраэдре, кубе, октаэдре, додекаэдре и икосаэдре, что закрепило за ними имя «платоновы», например, додекаэдр был известен издавна, как любимая игрушка этрусских детей, на протяжении 2500 лет назад. Это подтверждено находкой при раскопках в Монте Лоффа под Падуей (8, с. 82).

Неудивительно, что на протяжении веков к многогранникам проявлялся практический интерес. Например, куб и тетраэдр привлекались к созиданию строительства и на службу других сторон жизни людей. Египетские пирамиды поражают монументальностью простых форм. Однако, при рассмотрении, например, графических или бумажных моделей куба, тетраэдра, вызывается иное чувство и иное расположение к образу геометрической формы. В эпоху конструктивизма (20 век) архитектурное строительство и другие сферы материальной среды, откликались на социальные преобразования в обществе - поиск новых простых и выразительных форм.

Двойственные фигуры

Тема многогранников остаётся актуальной, в частности, при ознакомлении студентов с пропедевтикой художественного формообразования. В этой связи нельзя обойти вопрос двойственности геометрических фигур. Мы используем термин «двойственность» применительно к пространственным фигурам. В проективной геометрии двойственность трактуется следующим образом: «Каждому проективному предложению, относительно элементов (точек, прямых и плоскостей) пространства, соответствует второе предложение (двойственное), которое получается из первого предложения заменой в нём слова «точка» словом «плоскость» и слова «плоскость» словом «точка». При этом слово «прямая» не подвергается замене» (17, с. 92).

Представим двойственные многогранники (тела Платона). Тетраэдр - фигура состоит из четырёх точек (вершин), четырёх плоскостей (граней) и шести прямых (рёбер). Рис. 2 - тетраэдр и его развёртка.

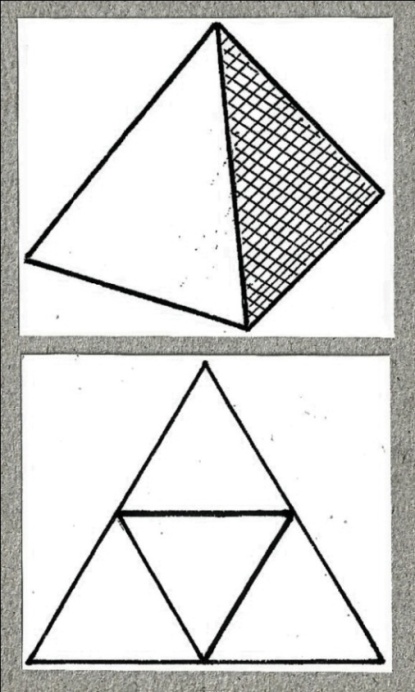
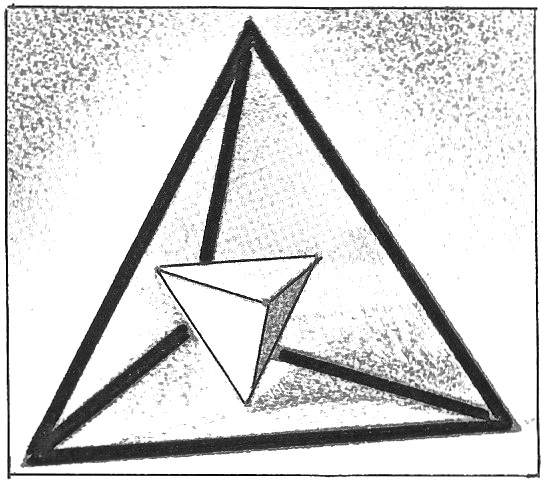
Рис. 2. Рис. 3 .

В популярной книге «Математический калейдоскоп», польского математика Гуго Штейнгауза, приведены модели пяти правильных многогранников. На их примере автор демонстрирует совпадение центров граней одного многогранника с вершинами другого, находящегося внутри его. Автор не отвлекается на характеристику двойственных пар пространственных тел. Однако, эти изображения являются наглядной иллюстрацией принципа двойственности (рис. 3, 5, 6а, 8, 10).

В соответствии с определением двойственности, на примере тетраэдра, произведём замену слов: вместо слова «точек»- слово «плоскостей», вместо слова «плоскостей» - слово «точек». Двойственная фигура будет состоять из четырёх плоскостей, четырёх точек и шести прямых. Становится очевидным, что тетраэдр является сам себе двойственный. На рисунке 3 изображена рёберная модель тетраэдра, внутри которой расположена двойственная фигура - тетраэдр. Его вершины принадлежат центрам четырёх граней исходного тетраэдра.

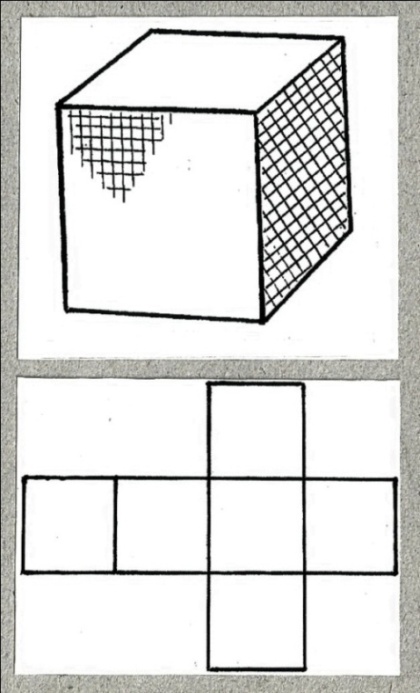
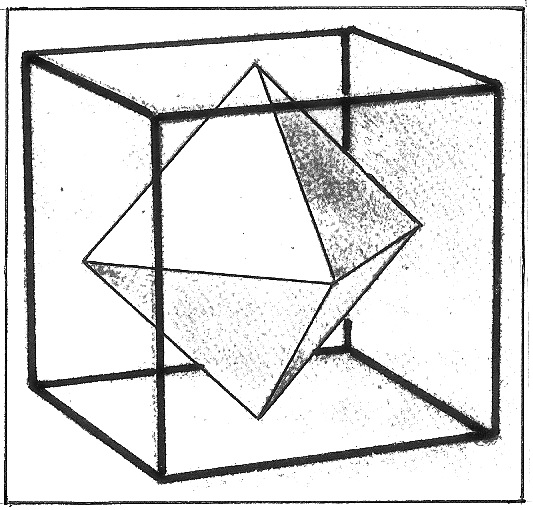
Рис. 4. Рис. 5.

Куб (гексаэдр) состоит из шести плоскостей (граней), восьми точек (вершин) и двенадцати прямых (рёбер). ( рис. 4).

В результате замены соответствующих слов, двойственная фигура должна состоять из шести точек (вершин), восьми плоскостей (граней) и двенадцати прямых (рёбер). Эту фигуру называют октаэдром. На рисунке 5 изображена рёберная модель куба. Внутри её размещён октаэдр, его вершины принадлежат центрам граней куба.

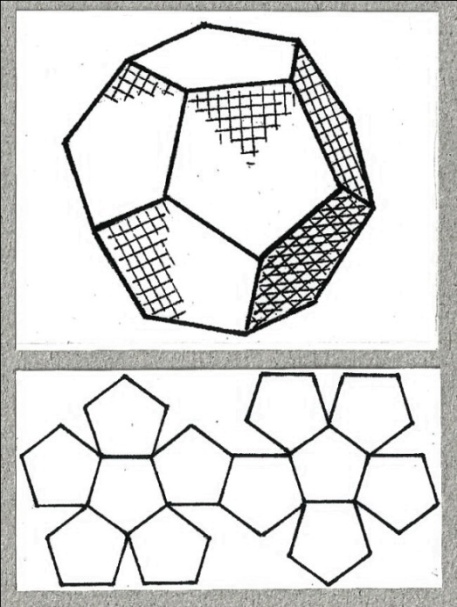
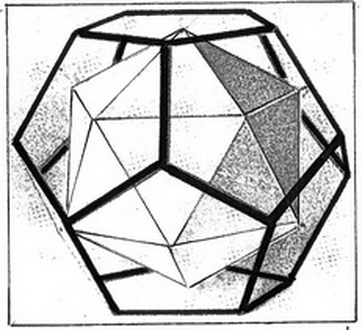
Рис. 6. Рис. 6а.

Додекаэдр - фигура состоит из двенадцати плоскостей (граней), двадцати точек (вершин) и тридцати прямых (рёбер). Рис. 6 - додекаэдр и его развёртка.

Заменив слова «плоскости» и «точки», получим двойственную фигуру икосаэдр. Он имеет двенадцать точек (вершин), двадцать плоскостей (граней) и тридцать прямых (рёбер). На рисунке 6а изображена рёберная модель додекаэдра. Внутри её размещена двойственная фигура - икосаэдр. Его вершины совпадают с центрами граней додекаэдра.

На рисунке 7 изображен знакомый нам двойственный многогранник куба - октаэдр. Его развёртку составляют два четырёхгранных угла.

Следующее изображение (рис. 8) - рёберная модель октаэдра, внутри которой размещен его двойник - куб. Вершины куба совпадают с центрами граней октаэдра.

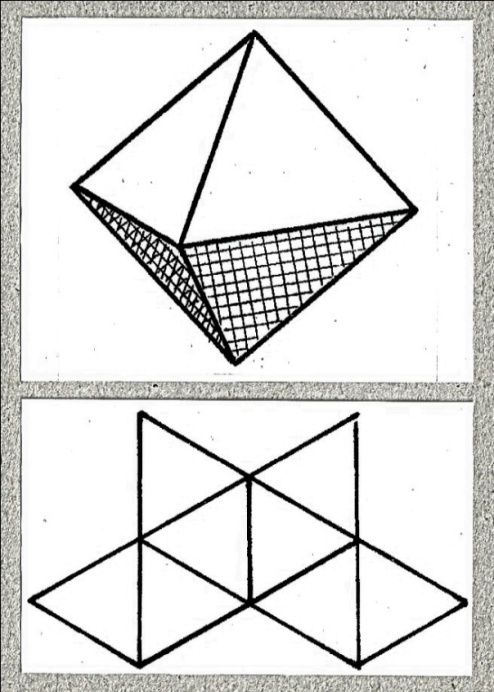
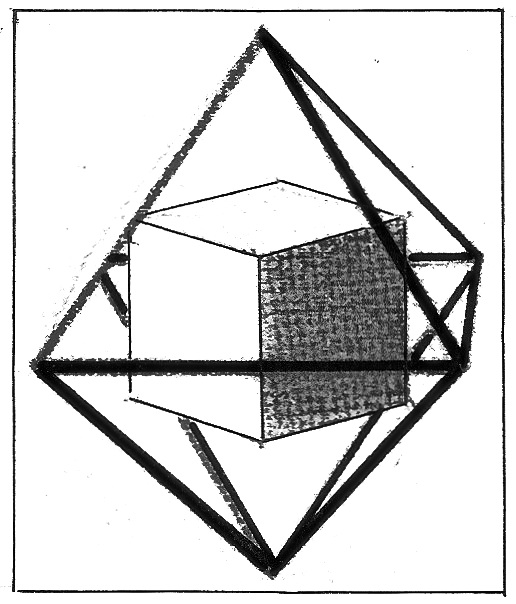
Рис. 7. Рис. 8.

Пятый многогранник – икосаэдр. Развёртка многогранника изображена на рисунке 9.

На рисунке 10 изображена двойственная фигура додекаэдра, расположенная внутри рёберной модели икосаэдра.

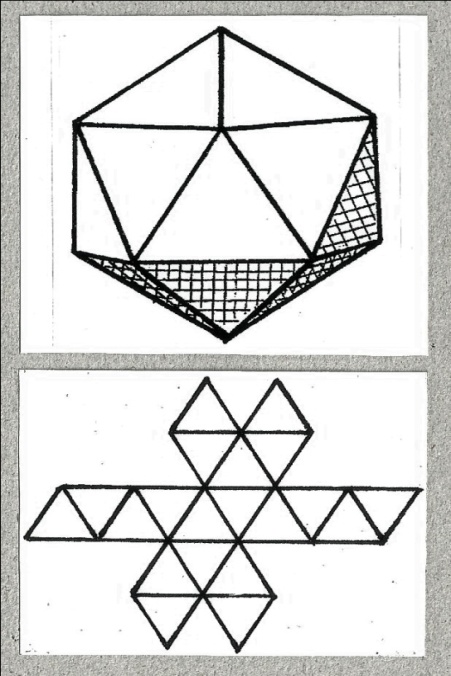
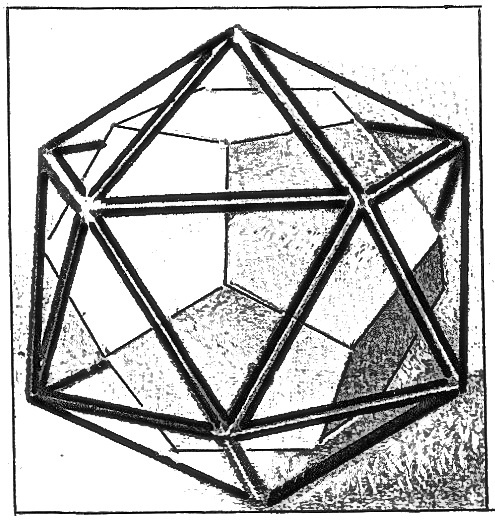
Рис. 9. Рис. 10.

Построение макета многогранника из бумаги не составляет особой сложности. Для этого необходимо создать соответствующую развёртку, изготовить из неё макет или использовать для тиражирования отдельных заготовок. Выбор того или иного подхода определяется самим исполнителем макета. В таком случае развёртки для макетирования многогранных тел можно применять отдельными фрагментами. Например, для построения макета куба достаточно фрагмента развёртки, состоящего из трёх квадратов. По нему тиражируется сколько угодно заготовок, если понадобиться иметь не один, а несколько кубов. В случае с октаэдром используется фрагмент развёртки, состоящий из четырёх равносторонних треугольников. Построенные две половины макета октаэдра будут напоминать четырёхугольные пирамиды. Воображаемые квадратные основания пирамид примыкают к экваториальной плоскости октаэдра. Она делит фигуру многогранника на две равные половины. Куб делится на равные половины координатными или диагональными плоскостями.

Фрагмент развёртки додекаэдра, у которого к сторонам пятиугольника примыкают пять аналогичных фигур, послужит для тиражирования двух заготовок. Таким образом, созданные из заготовок две трёхмерные формы, соединяются с помощью клея в одну многогранную модель двенадцатигранника.

Макет икосаэдра может быть создан из трёх заготовок. Одна из них получается тиражированием фрагмента развёртки, состоящего из десяти равносторонних треугольников и соединяющихся между собой в кольцеобразную форму. Две другие части тиражируются из одного звена развёртки, представляющего собой развёртку пятигранного угла. Его составляют пять равносторонних треугольников (граней икосаэдра).

В дальнейшем представим рёберно-сетчатые модели двойственной пары икосаэдра и додекаэдра. Во-первых, многогранники, созданные в рёберном исполнении, воспринимаются, так сказать, «прозрачными». Во-вторых, внутреннее пространство таких моделей обустраивается с помощью нитей, что придаёт им вид сетчатой структуры. В связи с этим рассмотрим простую модель, отражающую пространство усеченного куба (тела Архимеда) на следующих страницах.