Краткий конспект по курсу
«САПР»
Для специальности кафедры ТПЛА
Составитель:Шерышев А.Е.
Москва 2011
Цели и задачи курса.
Целью освоения дисциплины (модуля) «Системы автоматизированного проектирования РКТ » являются получения знания в области автоматизированного проектирования и разработки РКТ.
Для достижения поставленной цели при изучении дисциплины решаются следующие задачи
1. Усвоения знаний по основам «САПР»;
Привить навыки в организации собственного труда в области расчетных задач;
Привить навыки в работе с программным обеспечением при вычислительных расчетах;
Научить использовать полученные знания в практической работе;
Развить творческое мышление в области методов автоматизированного проектирования.
Раздел 1. Математические основы сапр (лекция на 2 час)
Координаты
Декартовая двухмерная система координат:
Полярная система координат:
Объемные системы координат (декартовые):
Цилиндрические системы координат:
Сферическая система координат:
Координаты технологические
Прямые
1.
- явный вид.
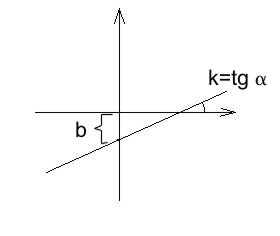
2.
- неявный вид, задан с тремя параметрами.
3.
- неявный вид, задан с четырьмя параметрами
и без теневого угла.
4.
- параметрический способ задания.
5.
- матричный способ задания.
6.
- параметрический способ задания.
-
число,
- единичный вектор.
Сплайн
Пусть на [a,b]
задана сетка
и значения сетки в узлах
.
Аппроксимируем на каждом i-ом отрезке в данной сетке кубическим полиномом:
При этом необходимо выполнять условия:
– нет разрыва;
–
как слева, так и справа одинаковы;
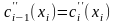– одинаковые касательные и радиус
кривизны на графике;
i=2 … n-1
Для выполнения необходимо условия, введем, что
и вторая производная
Тогда в аналитическом виде сплайн выглядит следующим образом:
Поверхности
Поверхность считается заданной, если относительно любой точки пространства можно однозначно и сколько угодно точно решить вопрос о ее принадлежность данной поверхности.
Поверхности могут быть в аналитической поверхности представлены в различных видах:
1. в явном виде:
z = f(x,y);
2. в неявном виде:
f(x,y,z) = 0;
3. параметрический вид:
4. векторно-численный вид:
Конусы.
Конус:
Эллиптический цилиндр:
Гиперболический цилиндр:
Параболический цилиндр:
Эллипсоид:
Гиперболоид:
Двухполостной гиперболоид:
Гиперболический гиперболоид:
,
где p>0; q>0;
Эллиптический гиперболоид:
,
где p>0; q>0;
Точечно-заданный способ задания. Поверхность, полученная полиномами Лагранжа.
Простейший алгоритм построения поверхности по исходному точечному базису заключается в обобщение методов Лагранжа для нахождения единственного полинома, который будет интерполировать все заданные точки.
Этот полином имеет вид:
Недостатком данного способа – задания поверхности - можно отметить, что при достаточно больших pи q, построенных, таким образом, что на поверхности появляются нежелательные осцеляции, что приводят к выявленным отделением ячеек, с малым количеством точек, описывающиеся каждую ячейку, это влечет за собой понижение степени полинома, описывающиеся данную поверхность, и количество данной поверхностей.
Уравнение поверхности в форме Безье.
Пусть кривая прямой, представляется в форме Безье характеристической ломаной, движется в направление “V”, каждая точка (вершина) характеристической ломаной проходит определенный путь, таким образом, получается каркас поверхности (формула) и т.д.
Уравнение полиноминальной поверхности в форме Берштейна-Безье будет иметь вид:
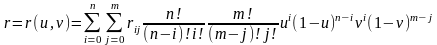
где
– вершина характеристик многогранника;m
– число вершин по направлению V;
n – число вершин по
направлению U; i
– текущая вершина по направлению U;j
– текущая вершина по направлению V;