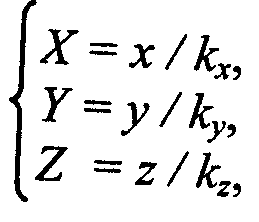Глава 2

Координатный метод

Координатный метод был введен в XVII веке французскими математиками I Р. Декартом и П. Ферма. На этом методе зиждется аналитическая геометрия, I которую можно считать фундаментом компьютерной графики. В современ­ной компьютерной графике широко используется координатный метод. Это­му есть несколько причин.

О Каждая точка на экране (или на бумаге при печати на принтере) задается координатами — например, пикселными.

О Координаты используются для описания объектов, которые будут ото­бражаться как пространственные. Например, объекты микромира, объек­ты на поверхности Земли, объекты космического пространства и тому по­добное. Даже тогда, когда отображается нечто, не имеющее привязки к положению в пространстве (например, случайные цветовые пятна в ка­ком-то видеоэффекте), то и здесь используются координаты для учета взаиморасположения отдельных элементов.

□ При выполнении многих промежуточных действий отображения исполь­зуют разные системы координат и преобразования из одной системы в другую.

2.1. Преобразование координат

Сначала рассмотрим общие вопросы преобразования координат. Пусть зада­на и-мерная система координат в базисе (k₁, k₂, …, k_n ), описывающая положе­ние точки в пространстве с помощью числовых значений k_i. В компьютер­ной графике чаще всего используется двумерная (n=2) и трехмерная (n=3) системы координат.

Если задать другую, N-мерную, систему координат в базисе (m₁, m₂, …, m_N) и поставить задачу определения координат в новой системе, зная координаты и старой, то решение (если оно существует) можно записать в таком виде:

где f_i— функция пересчета i-ой координаты, аргументы — координаты в сис­теме ki.

Можно поставить и обратную задачу — по известным координатам (m₁, m₂, ..., m_N) определить координаты (к₁, к₂ ..., к_n). Решение обратной задачи запи­шем так:

где F_i — функции обратного преобразования. В случае, когда размерности систем координат не совпадают (п ≠ N), осуще­ствить однозначное преобразование координат зачастую не удается. Напри­мер, по двумерным экранным координатам нельзя без дополнительных усло­вий однозначно определить трехмерные координаты отображаемых объектов. Если размерности систем совпадают (п = N), то также возможны случаи, ко­гда нельзя однозначно решить прямую или обратную задачи. Преобразование координат классифицируют:

□ по системам координат— например, преобразование из полярной систе­мы в прямоугольную;

□ по виду функций преобразования f_i

По виду функций преобразования различают линейные и нелинейные преоб­разования. Если при всех i = 1, 2, ..., N функции f_i — линейные относительно аргументов (к₁, к₂ .... к_n), то есть

где a_ij — константы, то такие преобразования называются линейными, а при п = N— аффинными.

Если хотя бы для одного i функция f_i— нелинейная относительно (k₁ , к₂,..., к_n), тогда преобразование координат в целом не линейно.

Например, преобразование

нелинейное, так как в выражении для Y присутствует ху.

Тем, кто интересуется математическими аспектами, относящимся к системам координат и преобразованиям систем координат, можно порекомендовать такие книги, как [16, 23].

Линейные преобразования наглядно записываются в матричной форме:

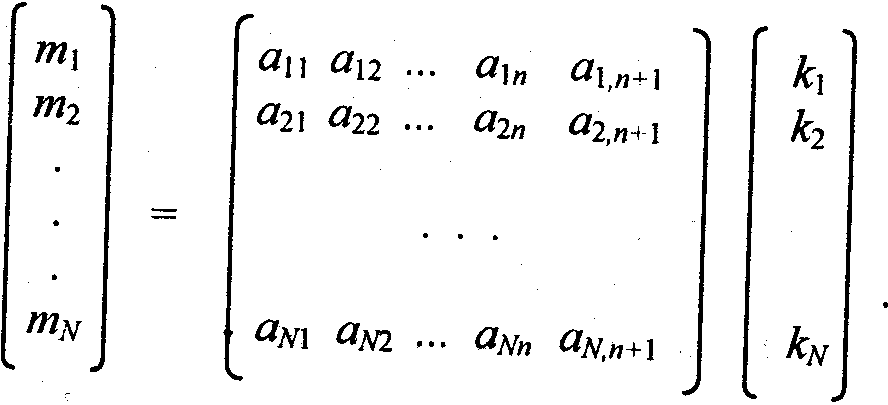
Здесь матрица коэффициентов (a_ij) умножается на матрицу-столбец (k_i) и в результате получается матрица-столбец (m_i).

Мы и далее часто будем использовать умножение матриц, поэтому сделаем небольшой экскурс в матричную алгебру. Для двух матриц А размером (т хп) и В размером (пxр):

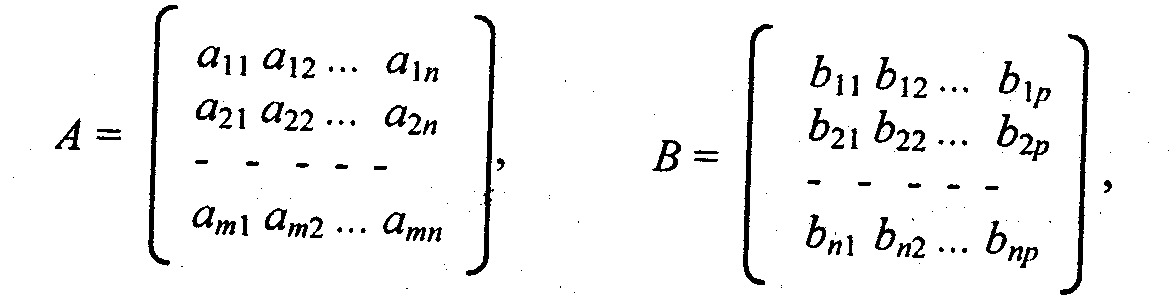
произведением матриц является матрица С = А В размером (т*р)

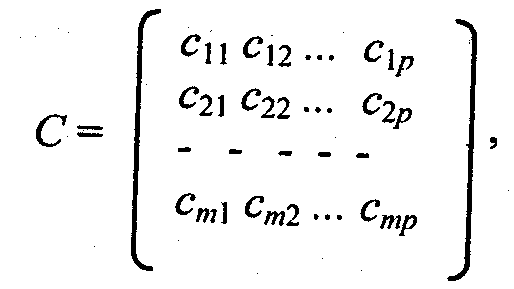
для которой элементы с_ij вычисляются по формуле

Правило вычисления элементов матрицы С можно легко запомнить по названию "строка на столбец". И действительно, для вычисления любого элемента c_ij необходимо умножить элементы i-й строки матрицы А на элементы j-го столбца матрицы В.

Произведение матриц определено только для случая, когда количество столбцов матрицы А равно количеству строк матрицы В.

Подробнее с матрицами вы можете ознакомиться в специальной математиче­ской литературе, например в [5].

Ну а теперь вернемся к преобразованиям координат. Рассмотрим более под­робно некоторые отдельные типы преобразований.

Аффинные преобразования на плоскости

Зададим некоторую двумерную систему координат (х, у). Аффинное преобра­зование координат (х, у) описывается формулами

где А, В, ..., F — константы. Значения (X, Y) можно трактовать как координа­ты в новой системе координат.

Обратное преобразование (X, Y) в (х, у) также является аффинным:

Аффинное преобразование удобно записывать в матричном виде. Константы А, В, ..., F образовывают матрицу преобразования, которая, будучи умножен­ная на матрицу-столбец координат (х, у), дает матрицу-столбец (X, Y). Однако для того, чтобы учесть константы С и F, необходимо перейти к так называе­мым однородным координатам — добавим строку с единицами в матрицах координат:

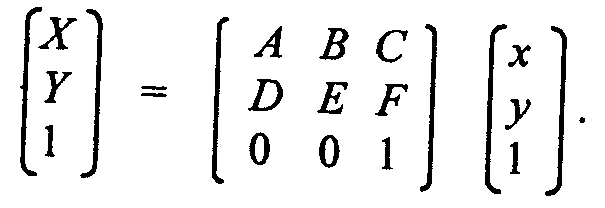
Матричная запись дает возможность наглядно описывать несколько преобра­зований, которые идут одно за другим. Например, если необходимо сначала выполнить преобразования

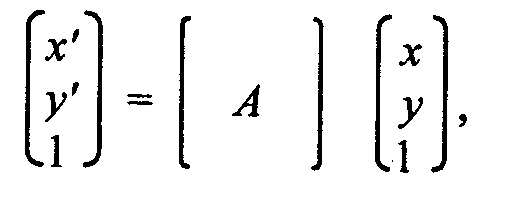
а потом — другое преобразование

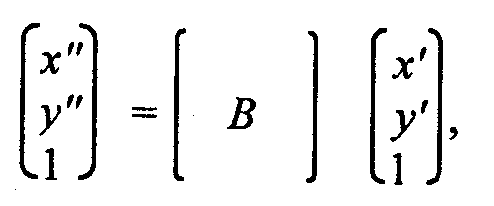
то это можно описать как

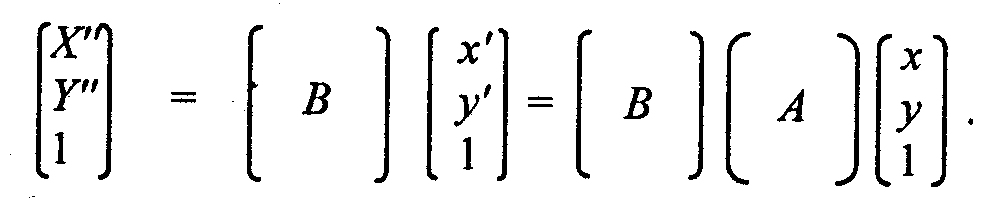
Однако вместо двух преобразований можно выполнить только одно

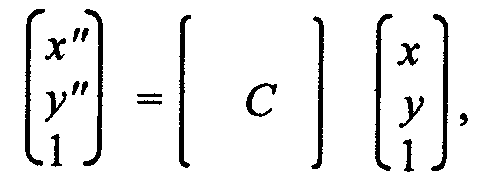
где матрица (C) равна произведению (В)(А).

Перемножение матриц выполняется так, как это принято в линейной алгебре.

Рассмотрим частные случаи аффинного преобразования.

1. Параллельный сдвиг координат (рис. 2.1).

В матричной форме:

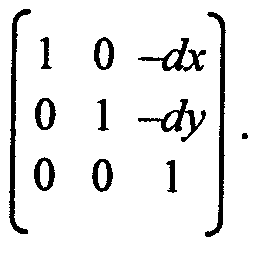
Обратное преобразование:

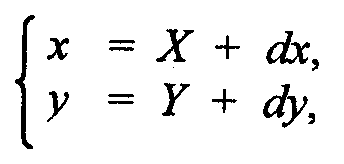
2. Растяжение-сжатие осей координат (рис. 2.2).

Обратное преобразование:

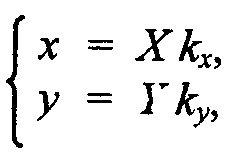
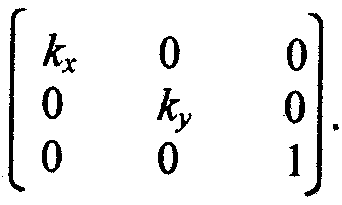
Коэффициенты к_х и к_у могут быть отрицательными. Например, к_х = -1 соот­ветствует зеркальному отражению относительно оси y

3. Поворот (рис. 2.3).

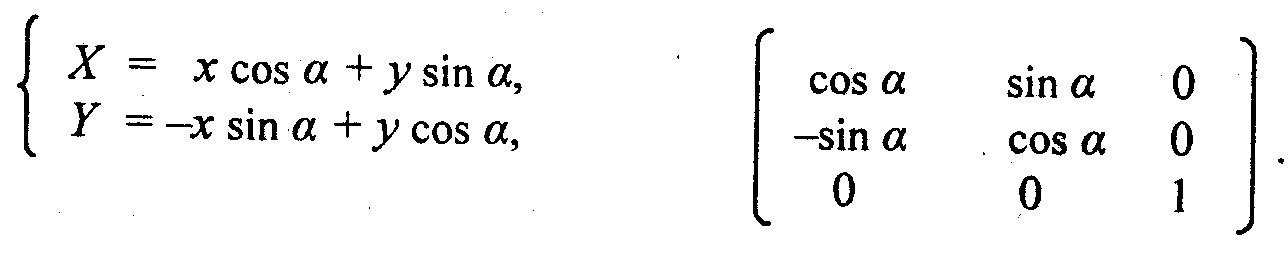
Обратное преобразование соответствует повороту системы (X, Y) на угол (-α).

Свойства аффинного преобразования.

□ Любое аффинное преобразование может быть представлено как последо­вательность операций из числа указанных простейших: сдвиг, растяже­ние/сжатие и поворот.

□Сохраняются прямые линии, параллельность прямых, отношение длин отрезков, лежащих на одной прямой, и отношение площадей фигур.

Трехмерное аффинное преобразование

Запишем в виде формулы:

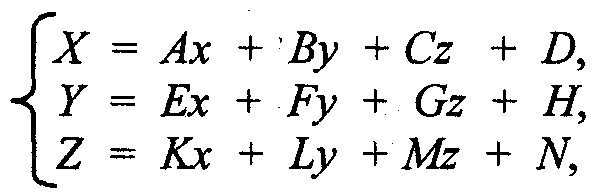
где А, B, ..., N — константы.

Дадим также в матричной форме:

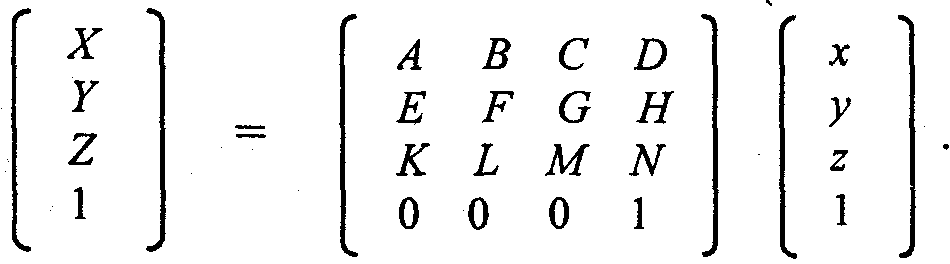
Для трехмерного пространства любое аффинное преобразование также мо­жет быть представлено последовательностью простейших операций. Рас­смотрим их.

1. Сдвиг осей координат соответственно на dx, dy, dz

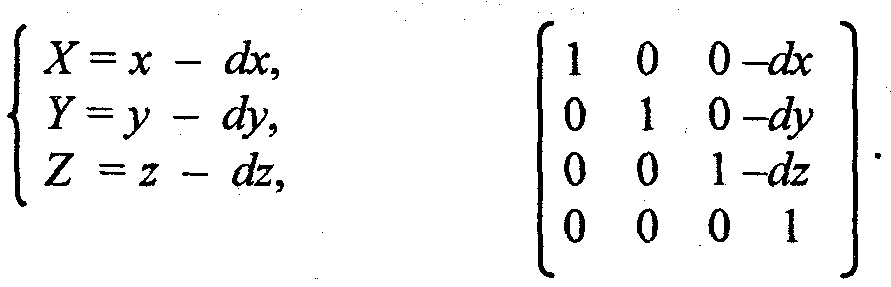
2. Растяжение-сжатие на к_x к_у, к_z: