1. Связь координат на меридианном эллипсе
Для установления связи между системами координат на меридианном эллипсе обратимся к рисунку 3. 2. Прежде определим связь широт с плоскими прямоугольными координатами.
Для геоцентрической широты имеем уравнение связи из рисунка
(
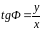3. 2 )
Для приведенной широты имеем
,
(
3. 3 )
откуда получаем выражение
(
3. 4 )
Сравнивая выражения ( 3. 2 ) и ( 3. 4 ), получаем уравнение связи геоцентрической и приведенной широт
.
(
3. 5 )
Для установления связи координат x, y с геодезической широтой B вспомним геометрический смысл первой производной. Если задано уравнение плоской кривой y = f ( x ) , то первая производная dy / dx равна тангенсу угла, образованного касательной к кривой в данной точке с положительным направлением оси абсцисс. Применительно к рисунку 3. 2 можем записать
.
(
3. 6 )
Уравнение меридианного эллипса в функции плоских прямоугольных координат имеет выражение ( 2. 1 ). Дифференцируем по переменной x это уравнение
,
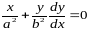откуда имеем для производной
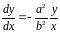. ( 3. 7 )
Приравнивая правые части уравнений ( 3. 6 ) и ( 3. 7 ), получаем
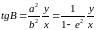. ( 3. 8 )
Учитывая выражения ( 3. 4 ) и ( 3. 5 ), можем записать следующие уравнения связи широт
;
;
.
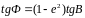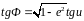( 3. 9
)
Используя полученные уравнения, а также имея в виду уравнения ( 3. 4 ), получаем выражения для плоских прямоугольных координат x, y в функции широт:
(
3. 10 )
(
3. 11 )
(
3. 12 )
3. 2. Пространственные координаты
Для определения положения точки Q на поверхности эллипсоида в сфероидической геодезии используют системы пространственных координат: геодезические ( B ), приведенные ( u ) и геоцентрические ( Ф ) широты и геодезические долготы L, а также декартовые координаты x, y, z . На рисунке 3. 1 меридианный эллипс определяемой точки PQ. Из сравнения рисунков 3. 1 и 3. 2 замечаем следующие уравнения связи прямоугольных пространственных x, y, z и в плоскости меридианного эллипса ( x ), ( y ) координат
.
(
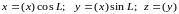3. 13 )
Подставляя сюда выражения для ( x ) и ( y ) из ( 3. 10 ) – ( 3. 12 ), несложно получить уравнения связи, например:
(
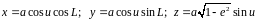3. 14 )
(
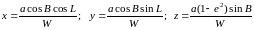3. 15 )
Здесь и в последующем мы используем общепринятое в геодезии обозначение выражения
,
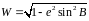которое называют первой основной функцией широты.
В настоящее время для решения геодезических задач все более используются спутниковые системы позиционирования, когда носителями координат являются созвездия специальных ИСЗ, находящихся на значительном удалении от поверхности земного эллипсоида. Если это удаление характеризуется геодезической высотой H, то уравнения связи пространственных прямоугольных и геодезических широт , долгот и высот принимают вид, следуемый из ( 3. 15 ), если к каждой из координат x, y, z прибавить проекции геодезической высоты H на соответствующие координатные оси
(
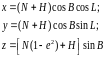3. 16 )
Здесь
принято обозначение:
- отрезок Qn
на рисунке 3. 1.- радиус первого вертикала.
На практике возникает задача вычисления
координат B,
L, H по известным
x, y, z.
Рассмотрим вывод формул для решения
этой задачи. Разделив второе уравнение
( 3. 16 ) на первое, получаем
(
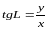3. 17 )
Возведя в квадрат первые два уравнения ( 3. 16 ) и найдя их сумму, получаем уравнение
,
(
3. 18 )
которое совместно с третьим из ( 3. 16 ) приводит к уравнению
,
(
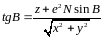3. 19 )
которое позволяет вычислить геодезическую широту методом последовательных приближений, которые будут сходящимися. Так, если требуется вычислить широту с точностью до 0. 0001// , достаточно трех приближений. Для удобства организации итерационных вычислений формулу (3. 19) можно преобразовать, переходя в правой части уравнения от sin B к tg B по формуле
.